L’analisi ammortizzata è usata per algoritmi che hanno operazioni costose che accadono solo raramente.

L’analisi della complessità ammortizzata è più comunemente usata con strutture dati che hanno uno stato che persiste tra le operazioni.L’idea di base è che un’operazione costosa può alterare lo stato in modo che il caso peggiore non possa ripetersi per molto tempo, ammortizzando così il suo costo.
Lasciamo che T1, T2, …, Tk siano le complessità di una sequenza di operazioni su una struttura dati. La complessità ammortizzata di una singola operazione in questa sequenza è (T1 + T2 + …+ Tk) / k.
Esempio: un array dinamico
In un array dinamico, gli elementi sono memorizzati all’inizio di un sottostante array fisso, e le posizioni rimanenti sono inutilizzate.
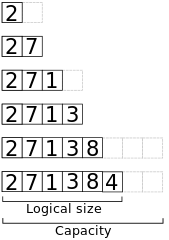
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Ecco una vista della memoria quando si aggiungono gli elementi 2, 7, 1, 3, 8, 4 ad un array inizialmente vuoto con capacità 2.
Worst-case time
La complessità temporale nel caso peggiore per aggiungere un elemento ad un array di lunghezza n, usando questo algoritmo, è Θ(n).Se l’array è pieno, l’algoritmo alloca un nuovo array di lunghezza 2n, e poi copia gli elementi dal vecchio array in quello nuovo.
Certo questo risultato è eccessivamente pessimistico.Le seguenti n operazioni di appendimento saranno molto più economiche – ognuna di esse verrà eseguita in tempo costante poiché la nuova matrice allocata ha spazio per tutti i nuovi elementi.
Tempo ammortizzato
Un’analisi del tempo ammortizzato dà una comprensione molto migliore dell’algoritmo.
Consideriamo una sequenza di n operazioni di appendimento, dove iniziamo con una matrice di lunghezza 1. Un’attenta analisi mostra che il tempo totale di queste operazioni è solo Θ(n).
- Ci sarà un totale di n operazioni di assegnazione e incremento a tempo costante.
- Il ridimensionamento avverrà solo alle operazioni 1, 2, 4, …, 2k, per un totale di 1 + 2 + 4 + …+ 2k = 2-2k – 1 operazioni di copia degli elementi a tempo costante. Poiché 2k ≤ n, questo è al massimo 2n – 1.
Quindi, la complessità temporale ammortizzata per una singola operazione di appendimento è Θ(1).
Più sull’analisi degli algoritmi

Complessità temporale: Conta i tuoi passi

Notazione Big O