Amortizovaná analýza se používá u algoritmů, které mají nákladné operace, k nimž dochází jen zřídka.

Amortizovaná analýza složitosti se nejčastěji používá u datových struktur, které mají stav, který přetrvává mezi operacemi.Základní myšlenkou je, že drahá operace může změnit stav tak, že se nejhorší případ nemůže po dlouhou dobu opakovat, čímž se amortizují její náklady.
Nechť T1, T2, …, Tk jsou složitosti posloupnosti operací na datové struktuře. Amortizovaná složitostjedné operace v této posloupnosti je(T1 + T2 + …+ Tk) / k.
Příklad: dynamické pole
V dynamickém poli jsou prvky uloženy na začátku základního pevného pole a zbývající pozice jsou nevyužity.
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Tady je pohled na paměť při přidávání prvků 2, 7, 1, 3, 8, 4do iniciačně prázdného pole s kapacitou 2. V tomto případě je složitost operace v této posloupnosti rovna(T1 + T2 + …+ Tk) / k.
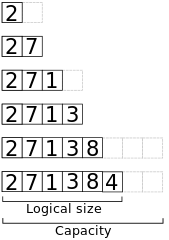
Čas v nejhorším případě
Časová složitost v nejhorším případě pro přidání prvkudo pole délky n pomocí tohoto algoritmu je Θ(n). pokud je pole plné, algoritmus alokuje nové pole délky 2n,a pak zkopíruje prvky ze starého pole do nového.
Klidně tento výsledek je příliš pesimistický.Následujících n operací připojování bude mnohem levnějších -každá z nich bude probíhat v konstantním čase, protože nově alokované pole má místo pro všechny nové prvky.
Amortisovaný čas
Amortisovaná časová analýza dává mnohem lepší představu o algoritmu.
Považujme posloupnost n operací připojování,kde začínáme s polem délky 1.
Podívejme se na posloupnost n operací připojování. Pečlivá analýza ukáže,že celkový čas těchto operací je pouze Θ(n).
- Proběhne celkem n operací přiřazení a inkrementace s konstantním časem.
- Ke změně velikosti dojde pouze při operacích 1, 2, 4, …, 2k, celkem tedy 1 + 2 + 4 + …+ 2k = 2-2k – 1 operací kopírování prvků s konstantním časem. Protože 2k ≤ n, je to nanejvýš 2n – 1.
Takže amortizovaná časová složitost pro jednu operaci přiložení je Θ(1).
Další informace o analýze algoritmu

Časová složitost: Počítejte kroky

Zápis velkého O
.