Hraniční vrstva je tenká vrstva viskózní kapaliny v blízkosti pevného povrchu stěny, která je v kontaktu s pohybujícím se proudem a v níž se (v rámci její tloušťky δ) rychlost proudění pohybuje od nuly u stěny (kde se proud díky své viskozitě „lepí“ na stěnu) až po Ue na hranici, což přibližně (s chybou 1 %) odpovídá rychlosti volného proudu (viz obrázek 1). Přísně vzato je hodnota δ libovolná, protože třecí síla, závislá na molekulární interakci mezi tekutinou a pevným tělesem, klesá se vzdáleností od stěny a v nekonečnu se rovná nule.
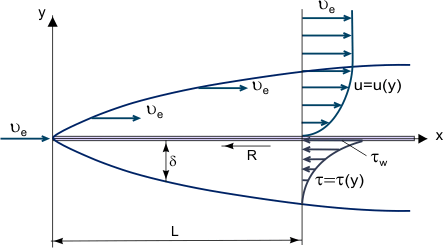
Obrázek 1. Růst mezní vrstvy na ploché desce.
Základní pojem mezní vrstvy navrhl L. Prandtl (1904), definuje mezní vrstvu jako vrstvu tekutiny vznikající při proudění s velmi vysokým Reynoldsovým číslem Re, tj. s relativně nízkou viskozitou ve srovnání se setrvačnými silami. To se projevuje, když jsou tělesa vystavena proudu vzduchu s vysokou rychlostí nebo když jsou tělesa velmi velká a rychlost proudu vzduchu je střední. V tomto případě může být v relativně tenké mezní vrstvě třecí smykové napětí (viskózní smyková síla): τ = η (kde η je dynamická viskozita; u = u(y) – „profil“ podélné složky rychlosti mezní vrstvy, viz obrázek 1) velmi velké; zejména u stěny, kde u = 0 a τw = ηw, přestože samotná viskozita může být poměrně malá.
Je možné zanedbat síly tření mimo mezní vrstvu (ve srovnání se silami setrvačnosti) a na základě Prandtlovy koncepce uvažovat dvě oblasti proudění: mezní vrstvu, kde jsou účinky tření velké, a téměř inviscidní jádro proudění. Za předpokladu, že mezní vrstva je velmi tenká vrstva (δ << L, kde L je charakteristický lineární rozměr tělesa, nad nímž proudění probíhá, nebo kanálu obsahujícího proudění, přičemž její tloušťka klesá s růstem Re, obr. 1), lze odhadnout řádovou velikost tloušťky mezní vrstvy z následujícího vztahu:
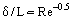
Příklad když letadlo letí rychlostí Ue = 400 km/h, tloušťka mezní vrstvy na odtokové hraně křídla o délce profilu 1 metr je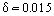 m. Jak bylo experimentálně zjištěno, na vstupní části tělesa vzniká laminární mezní vrstva. Postupně se vlivem některých destabilizujících faktorů stává mezní vrstva nestabilní a dochází k přechodu mezní vrstvy do režimu turbulentního proudění. Speciální experimentální výzkumy prokázaly existenci přechodové oblasti mezi turbulentní a laminární oblastí. V některých případech (například při vysoké úrovni turbulence vnějšího proudění) se mezní vrstva stává turbulentní bezprostředně za bodem stagnace proudění. Za určitých podmínek, například při silném poklesu tlaku, dochází při zrychlujícím se turbulentním proudění k inverznímu jevu, a to k relaminarizaci proudění.
m. Jak bylo experimentálně zjištěno, na vstupní části tělesa vzniká laminární mezní vrstva. Postupně se vlivem některých destabilizujících faktorů stává mezní vrstva nestabilní a dochází k přechodu mezní vrstvy do režimu turbulentního proudění. Speciální experimentální výzkumy prokázaly existenci přechodové oblasti mezi turbulentní a laminární oblastí. V některých případech (například při vysoké úrovni turbulence vnějšího proudění) se mezní vrstva stává turbulentní bezprostředně za bodem stagnace proudění. Za určitých podmínek, například při silném poklesu tlaku, dochází při zrychlujícím se turbulentním proudění k inverznímu jevu, a to k relaminarizaci proudění.
Přes svou relativní tenkost je mezní vrstva velmi důležitá pro iniciaci procesů dynamické interakce mezi prouděním a tělesem. Mezní vrstva určuje aerodynamický odpor a vztlak letícího dopravního prostředku nebo energetické ztráty při proudění tekutin v kanálech (v tomto případě hydrodynamická mezní vrstva, protože existuje také tepelná mezní vrstva, která určuje termodynamickou interakci Heat Transfer).
Výpočet parametrů mezní vrstvy je založen na řešení rovnic získaných z Navierových-Stokesových rovnic pro pohyb viskózní tekutiny, které jsou nejprve značně zjednodušeny s ohledem na tenkost mezní vrstvy.
Řešení navržené L. Prandtlem je v podstatě prvním členem mocninného rozkladu Navierovy-Stokesovy rovnice, přičemž rozklad řady se provádí pro mocniny bezrozměrného parametru (δ/L). Menší parametr v tomto členu je v nulové mocnině, takže rovnice mezní vrstvy je nulovou aproximací v asymptotickém rozšíření (při velkém Re) rovnice mezní vrstvy (asymptotické řešení).
Transformaci Navierovy-Stokesovy rovnice na rovnice mezní vrstvy lze demonstrovat odvozením Prandtlovy rovnice pro laminární mezní vrstvu ve dvourozměrném nestlačitelném proudění bez sil tělesa.
V tomto případě bude soustava Navierových-Stokesových rovnic:

Po vyhodnocení řádu velikosti některých členů rov. (2) a zanedbání malých členů se soustava Prandtlových rovnic pro laminární mezní vrstvu stane:

v níž x, y jsou podélné a příčné souřadnice (obr. 1); v je složka rychlosti podél osy „y“; p, tlak; t, čas; a n kinematická viskozita.
Pomezní vrstva je tenká a rychlost na jejím vnějším okraji Ue lze dostatečně a přesně určit jako rychlost proudění ideální (inviscidní) kapaliny podél stěny vypočtenou až do prvního přiblížení, aniž by se zohlednilo zpětné působení mezní vrstvy na vnější proudění. Podélný tlakový gradient = (při p(y) = const) v rovnici (3) lze znázornit z Eulerovy pohybové rovnice ideální tekutiny. Z výše uvedeného vyplývá, že Prandtlovy rovnice v konečné podobě budou zapsány jako:

Jedná se o soustavu parabolických nelineárních parciálních diferenciálních rovnic druhého řádu, které se řeší s počátečními a okrajovými podmínkami


Soustava rovnic (4) se zapisuje pro skutečné hodnoty složek rychlosti u a v. Pro zobecnění rovnic získaných pro turbulentní proudění je třeba použít známý vztah mezi skutečnými, zprůměrovanými a pulzujícími složkami parametrů turbulentního proudění. Například pro složky rychlosti existují vztahy spojující skutečné u a v, průměrné ū a a pulzující složky u‘ a v‘:
a pulzující složky u‘ a v‘:

Po určitých úpravách lze ze soustavy (3) získat další soustavu rovnic, zejména pro ustálené proudění:
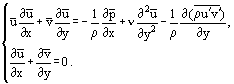
Při použití následujícího vztahu pro třecí smykové napětí v mezní vrstvě:
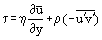
a s přihlédnutím k tomu, že v laminární mezní vrstvě u = u‘ a je možné přepsat Prandtlovy rovnice do tvaru platného pro laminární i turbulentní proudění:
je možné přepsat Prandtlovy rovnice do tvaru platného pro laminární i turbulentní proudění:
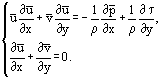
Nejjednodušší řešení bylo získáno pro laminární mezní vrstvu na tenké ploché desce při dvourozměrném paralelním proudění nestlačitelné tekutiny (obrázek 1). V tomto případě odhad řádu velikosti členů rovnic: x ~ L, y ~ δ, δ ~ umožňuje spojit proměnné x a y do jednoho vztahu
umožňuje spojit proměnné x a y do jednoho vztahu

a redukovat řešení rovnice (8) (při dp/dx = 0) na určení závislostí u a v na novém parametru ξ. Na druhé straně lze pomocí známých vztahů mezi složkami rychlosti u, v a proudovou funkcí ψ

získat jednu obyčejnou nelineární diferenciální rovnici třetího řádu, místo soustavy parciálních diferenciálních rovnic (8)

Zde je f(ξ) neznámá funkce proměnné ξ: f = ƒ =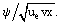
První numerické řešení rovnice: f = ƒ =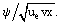
První numerické řešení rovnice (10) získal Blasius (1908) za okrajových podmínek odpovídajících fyzikálním podmínkám mezní vrstvy při y = 0: u = 0, v = 0; při y → ∞; u → Ue (Blasiusova mezní vrstva).
Obrázek 2 porovnává výsledky Blasiusova řešení (plná čára) s experimentálními daty. Na základě těchto údajů je možné vyhodnotit tloušťku viskózní mezní vrstvy. Při ξ  2,5, (u/Ue
2,5, (u/Ue 0,99) (obr. 2); následně ze vzorce (9) dostaneme:
0,99) (obr. 2); následně ze vzorce (9) dostaneme:

Obrázek 2.
Z Blasiových numerických výpočtů hodnoty druhé derivace funkce f(ξ) při smykovém napětí ve stěně vyplývá v tomto případě vztah:

Třecí síla R, působící na obou stranách desky délky L (obr. 1), se rovněž určí z rovnice. (11):

jako u součinitele tření pro ploché desky:
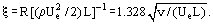
Přestože jsou Prandtlovy rovnice mnohem jednodušší než Navier-Stokesovy rovnice, jejich řešení bylo získáno pro omezený počet problémů. Pro mnoho praktických problémů není nutné určovat rychlostní profily v mezní vrstvě, pouze tloušťku a smykové napětí. Tento druh informací lze získat řešením integrální hybnostní rovnice

Integrální vztah (12) platí jak pro laminární, tak pro turbulentní mezní vrstvu.
Funkce, které nebyly a priori známy, ale které charakterizují rozložení parametrů tekutiny po tloušťce vrstvy δ, jsou pod integrálem v rovnici (12). A chyba výpočtu integrálu je menší než chyba přibližně předpokládané integrální funkce ρu = ρu(y). To vytváří podmínky pro vývoj přibližných metod výpočtu parametrů mezní vrstvy, které jsou časově méně náročné než přesné metody integrace Prandtlových rovnic. Základní koncepci poprvé navrhl T. von Karman, který zavedl takovou libovolnou tloušťku vrstvy δ*
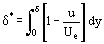
a tloušťku posunu hybnosti δ**
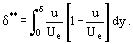
takto můžeme transformovat rov. (12) pro dvourozměrnou mezní vrstvu nestlačitelné kapaliny na:

V rovnici (15) jsou tři neznámé funkce, a to δ* = δ*(x), δ** = δ**(x) a τw = τw(x) .
Řešení obyčejné diferenciální rovnice, jako je rovnice (12), je v souladu s pravidly pro rovnice (15). (15) obvykle vyžaduje předpoklad (nebo znázornění) rozložení rychlostí (rychlostního profilu) v celé tloušťce mezní vrstvy jako funkce některých charakteristických parametrů (tvarových parametrů) a také vyžaduje použití empirických údajů o vztahu mezi součinitelem tření Cf = 2τw/(ρU2e) a libovolnou tloušťkou mezní vrstvy (zákon tření).
Některé konkrétní fyzikální vysvětlení lze uvést, pokud jde o hodnoty δ* a δ**. Integrální funkce v rovnici (13) obsahuje po přeuspořádání člen (Ue – u), který charakterizuje pokles rychlosti. Integrál v rovnici (14) lze tedy považovat za míru poklesu rychlosti proudění přes mezní vrstvu ve srovnání s dokonalým prouděním kapaliny při rychlosti Ue. Na druhé straně lze hodnotu δ* považovat za míru odchylky podél normály ke stěně (podél osy „y“) vnější čáry proudění pod vlivem třecích sil. Z této úvahy o integrální struktuře rovnice (14) lze vyvodit, že δ** charakterizuje pokles hybnosti v mezní vrstvě pod vlivem tření.
Platí následující vztahy:

kde H je tvarový parametr rychlostního profilu mezní vrstvy. Například pro lineární rozdělení u = ky,
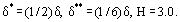
V současné době se pro předpověď parametrů turbulentní mezní vrstvy hojně používají tzv. poloempirické teorie. V tomto případě se předpokládá, že celkové třecí napětí τ v turbulentní mezní vrstvě je součtem

Zde τT je přídavné (turbulentní nebo Reynoldsovo) třecí napětí, zejména v nestlačitelném proudění viz rovnice. (7).
viz rovnice. (7).
Toto zobrazení přímo souvisí se soustavou pohybových rovnic v mezní vrstvě (6). Ve stlačitelné mezní vrstvě lze pulzace hustoty považovat za důsledek pulzací teploty

kde β = (1/T) je koeficient objemové roztažnosti.
K určení τT se používají další poloempirické hypotézy o turbulentním přenosu hybnosti. Například,

kde ηT je dynamický součinitel turbulentní viskozity zavedený J. Boussinesqem v roce 1877.
Na základě konceptu podobnosti molekulární a turbulentní výměny (teorie podobnosti) zavedl Prandtl hypotézu délky míchání (die Mischungsweg). Směšovací délka 1 je dráha, kterou konečný objem tekutiny („mol“) projde z jedné vrstvy středního pohybu do druhé, aniž by se změnila jeho hybnost. V souladu s touto podmínkou odvodil rovnici, která se ukázala být zásadní pro teorii mezních vrstev:

Pro turbulentní oblast mezní vrstvy proudění u stěny je L. Prandtl považoval za délku 1 úměrnou y

kde κ je empirická konstanta.
V blízkosti stěny, kde ηT << η, je určujícím faktorem viskózní molekulární tření. Tloušťka této části mezní vrstvy δ1, která se nazývá laminární nebo viskózní podvrstva, je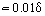 . Mimo tuto podvrstvu se hodnota ηT zvyšuje a dosahuje hodnot o několik řádů větších než η. Tomu odpovídá, že v této zóně mezní vrstvy známé jako turbulentní jádro je τT > 0 = η. Někdy se turbulentní jádro dělí na nárazníkovou zónu, kde je laminární a turbulentní tření srovnatelné hodnoty, a rozvinutou zónu, kde τT >> τ0. Pro tuto oblast lze po integraci rovnice (18) a s přihlédnutím k rovnici (19) odvodit výraz pro logaritmický rychlostní profil:
. Mimo tuto podvrstvu se hodnota ηT zvyšuje a dosahuje hodnot o několik řádů větších než η. Tomu odpovídá, že v této zóně mezní vrstvy známé jako turbulentní jádro je τT > 0 = η. Někdy se turbulentní jádro dělí na nárazníkovou zónu, kde je laminární a turbulentní tření srovnatelné hodnoty, a rozvinutou zónu, kde τT >> τ0. Pro tuto oblast lze po integraci rovnice (18) a s přihlédnutím k rovnici (19) odvodit výraz pro logaritmický rychlostní profil:
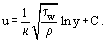
Použijeme-li bezrozměrné (nebo univerzální) souřadnice.

kde je takzvaná dynamická rychlost (nebo rychlost tření), rovnice (18) je rovnice (19). (20) lze přepsat v následujícím tvaru:
je takzvaná dynamická rychlost (nebo rychlost tření), rovnice (18) je rovnice (19). (20) lze přepsat v následujícím tvaru:
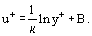
Zobrazením rozložení rychlostí v univerzálních souřadnicích a matematickými modely pro koeficient turbulentní viskozity se podrobněji zabývá kapitola Turbulentní proudění.
Jedna ze současných verzí semi-empirické teorie turbulentní mezní vrstvy, kterou vypracoval S. S. Kutateladze a A. I. Leontiev vychází z tzv. asymptotické teorie turbulentních mezních vrstev při Re → ∞, kdy tloušťka laminární (viskózní) podvrstvy δ1 klesá rychleji než δ, v důsledku čehož (δ1/δ) → 0.
Za těchto podmínek se vyvíjí turbulentní mezní vrstva s „mizivou viskozitou“. V této vrstvě je η → 0, ale není rovno nule a v tomto ohledu se vrstva liší od dokonalého proudění tekutiny. Pojem zákona relativního tření, který zavedli S. S. Kutateladze a A. I. Leontiev (1990), udává
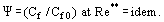
Zákon je definován jako poměr součinitele tření Cf pro uvažované podmínky k hodnotě Cf0 pro „standardní“ podmínky na ploché, nepropustné desce obtékané nestlačitelným, izotermickým prouděním, přičemž oba součinitele jsou získány pro Re** = Ueδ**/ν. Ukazuje se, že při Re → ∞; η → 0; a Cf → 0 má relativní změna součinitele tření pod vlivem takových rušivých faktorů, jako je gradient tlaku, stlačitelnost, neizotermnost, vstřikování (sání) přes porézní stěnu atd., konečnou hodnotu.
Rovnice odvozené pro výpočet hodnoty Ψ mají jednu důležitou vlastnost, která činí Ψ nezávislým na empirických konstantách turbulence. V souladu se základní koncepcí integrálního „přístupu“ se integrální rovnice hybnosti transformuje na:
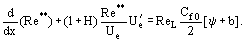
Zde, ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) jsou parametry propustnosti pro případ vstřikování plynu o hustotě ρw propustnou stěnou rychlostí vw. Pro určení funkce Re** = Re**
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) jsou parametry propustnosti pro případ vstřikování plynu o hustotě ρw propustnou stěnou rychlostí vw. Pro určení funkce Re** = Re** je nutné vypočítat rozdělení
je nutné vypočítat rozdělení Pro tento účel platí princip superpozice rušivých faktorů
Pro tento účel platí princip superpozice rušivých faktorů

V rov. 24 představuje každý násobitel relativní zákon tření, přičemž se zohledňuje vliv jednoho z rušivých faktorů, mezi nimiž jsou stlačitelnost ΨM, teplotní (nebo entalpický) náběh ΨT, vstřik ΨB, tlakový gradient ΨP a další.
Základní pojmy mezní vrstvy vytvářejí podmínky pro vysvětlení takových jevů, jako je oddělení proudění od povrchu vlivem setrvačnosti proudění, zpomalení viskózního proudění stěnou a nepříznivý gradient tlaku působící ve směru proti proudu = 0 nebo < 0.
Působí-li nepříznivý tlakový gradient v místě povrchu mezi úseky „1-4“ (viz obrázek 3), rozložení rychlostí u = u(x,y) v mezní vrstvě se postupně mění; stává se „méně plným“, snižuje se sklon v proudech tekutiny, které jsou blíže ke stěně a mají menší množství kinetické energie (viz tvary rychlostního profilu na obrázku 3), které pronikají daleko po proudu do oblasti zvýšeného tlaku. V některých úsecích, například v úseku „4“, se částice kapaliny, které se nacházejí na proudové čáře „a-a“ (tečkovaná čára na obrázku 3) – po úplném vyčerpání zásoby kinetické energie zpomalují (ua = 0).
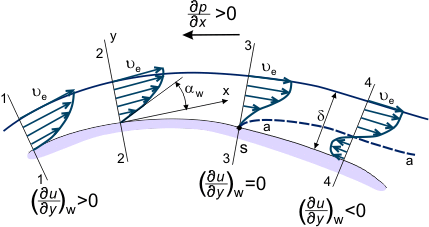
Obrázek 3. Mezní vrstva při proudění nad zakrytým povrchem.
Statický tlak a hodnota tlakového gradientu se v tloušťce mezní vrstvy nemění. Proto se částice kapaliny, které jsou blíže ke stěně než linie „a-a“ a mají ještě menší množství energie, začnou pod vlivem tlakového gradientu v úseku „4-4“ pohybovat opačným směrem (viz obrázek 3). Platí tedy vztah:

Takto se v některých místech povrchu mění rychlostní profil. Tato změna je charakterizována změnou znaménka derivace w z kladného (úsek 2, obrázek 3) na záporné (úsek 4). Samozřejmě je také možné definovat úsek, kde w = 0 (úsek 3, obrázek 3). Tento úsek se označuje jako úsek oddělení mezní vrstvy (odpovídajícím způsobem je bod „S“ na povrchu tohoto úseku bodem oddělení). Je charakterizován vznikem reverzní zóny proudění – proudění kolem tělesa již není plynulé, mezní vrstva se značně zhušťuje a linie vnějšího proudění se odchylují od povrchu obtékaného tělesa. Směrem dolů od bodu separace není rozložení statického tlaku v celé tloušťce vrstvy ustálené a rozložení statického tlaku podél povrchu neodpovídá rozložení tlaku ve vnějším, inviscidním proudění.
Po separaci následuje rozvoj zón zpětného proudění a vírů, v nichž se kinetická energie dodaná z vnějšího proudění vlivem třecích sil mění na teplo. Oddělení proudění, doprovázené rozptylem energie v zónách zpětného proudění, má za následek takové nežádoucí účinky, jako je zvýšení odporu letících vozidel nebo hydraulické ztráty v kanálech.
Na druhé straně se oddělené proudění používá v různých zařízeních pro intenzivní míchání kapaliny (například pro zlepšení míchání paliva a vzduchu ve spalovacích komorách motorů). Při proudění viskózních kapalin v kanálech s proměnným průřezem (střídavý tlakový gradient) může být separační zóna lokální, pokud za difuzorovou částí následuje konfuzorová část, kde se oddělené proudění opět připojí k povrchu (viz obrázek 4a). Když se proudění oddělí od odtokové hrany tělesa (například od odtokové hrany křídla), vytvoří se tzv. wake „spojením“ mezních vrstev (viz obrázek 4b).
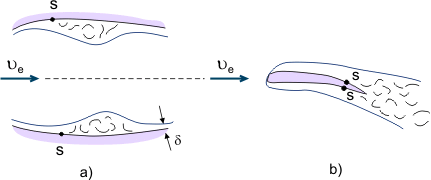
Obrázek 4. Jevy oddělování mezních vrstev.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. and Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.
.