Cíle výuky
- Poznat sítě.
- Použít sítě k zobrazení hranolů.
- Zjistit povrch hranolu.
- Zjistit povrch válce.
- Zjistit povrch koule.
Sítě
Jedním z posledních způsobů zobrazení tělesa je použití sítě. Pokud vystřihnete síť, můžete ji složit do modelu útvaru. Sítě lze také použít k analýze jednoho tělesa. Zde je příklad sítě pro krychli.
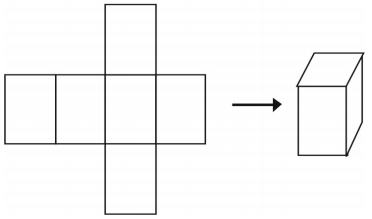
Je více způsobů, jak vytvořit síť pro jeden útvar.
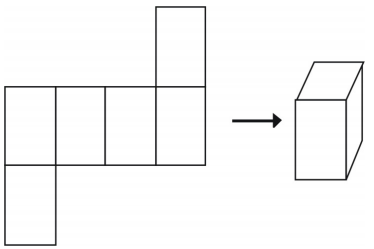
Ne všechna uspořádání však vytvoří krychli.
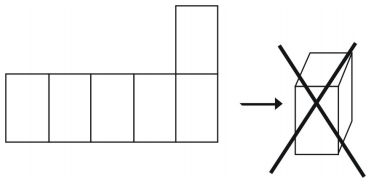
Příklad 1
Jaký útvar síť vytvoří? Nakresli tento útvar.
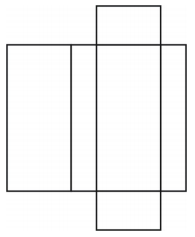
Síť vytvoří obdélníkový hranol ve tvaru krabice, jak je znázorněno na obrázku.
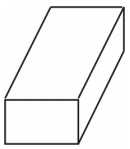
Příklad 2
Jaký druh sítě můžeš nakreslit, aby znázorňovala zobrazený útvar? Nakreslete síť.
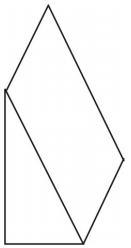
Na obrázku je znázorněna síť pro hranol. Je možné použít i jiné sítě.
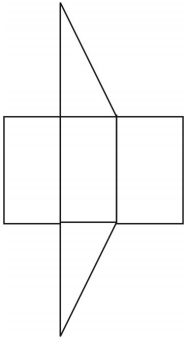
Přehledová cvičení
Nakresli síť pro každý z následujících objektů:
Odpovědi
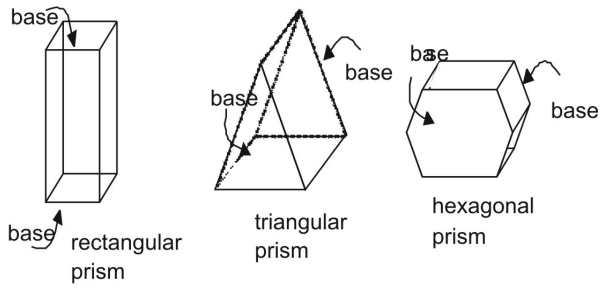
Hranoly
Hranol je trojrozměrný útvar s dvojicí rovnoběžných a shodných konců neboli podstav. Strany hranolu jsou rovnoběžníky. Hranoly se označují podle podstavy.
Povrch hranolu pomocí sítě
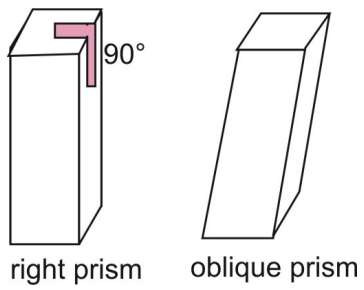
Výše uvedené hranoly jsou pravé hranoly. V pravém hranolu jsou boční strany kolmé k podstavám hranolu. Porovnejte pravý hranol se šikmým hranolem, u kterého strany a podstavy nejsou kolmé.
Dva postuláty, které se vztahují k ploše, jsou postulát shodnosti plochy a postulát sčítání plochy.
K nalezení povrchu pravého hranolu můžete použít síť a postulát o sčítání ploch.
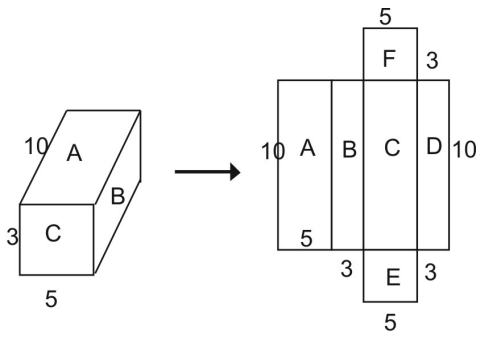
Ze sítě vidíš, že plocha celého hranolu se rovná součtu útvarů, které tvoří síť:
Celková plocha = plocha A + plocha B + plocha C + plocha D + plocha E + plocha F
Pomocí vzorce pro plochu obdélníku vidíš, že plocha obdélníku A je:
A = l – w
A = 10 – 5 = 50 čtverečních jednotek
Podobně dosadíme plochy ostatních obdélníků zpět do výše uvedené rovnice.
Celková plocha = plocha A + plocha B + plocha C + plocha D + plocha E + plocha F
Celková plocha = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3) + (5 – 5). 3)
Celkový povrch = 50 + 30 + 50 + 30 + 15 + 15
Celkový povrch = 190 čtverečních jednotek
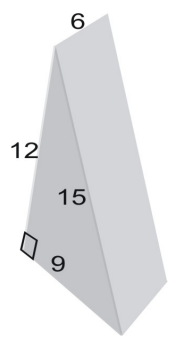
Příklad 3
Pomocí sítě zjistíme povrch hranolu.
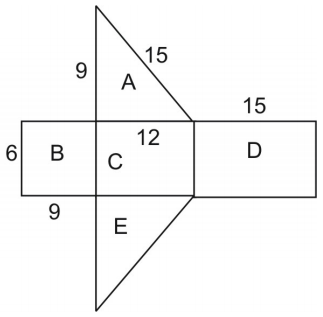
Plocha sítě se rovná ploše povrchu hranolu. Pro zjištění plochy trojúhelníku použijeme vzorec:
\dispozice{A}=\frac{1}{2}hb\\ kde h je výška trojúhelníku a b je jeho základna.
Poznamenejme, že trojúhelníky A a E jsou shodné, takže plochu trojúhelníku A můžeme vynásobit dvěma.
\displaystyle\text{area}=\text{area }A+\text{area }B+\text{area }C+\text{area }D+\text{area }E\
\displaystyle\text{ }=2(\text{area }A)+\text{area }. }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\
Thus, plocha je 324 čtverečních jednotek.
Přehledová cvičení
Pro každou z následujících úloh najděte povrch jsou a pomocí metody sítí a obvod


- Podstavou hranolu je pravoúhlý trojúhelník, jehož odvěsny jsou 3 a 4 a výška zobrazeného hranolu je 20. Jaká je jeho výška? Jaký je celkový povrch hranolu?
- Pravý šestiboký hranol je vysoký 24 cm a jeho podstavy jsou pravidelné šestiúhelníky o straně 8 cm. Jaký je celkový povrch hranolu?
- Jaký je objem hranolu v úloze č. 4?
V následujících otázkách má stodola tvar pětibokého hranolu s rozměry uvedenými ve stopách:

- Kolik čtverečních stop (bez střechy) je na povrchu stodoly, kterou je třeba vymalovat?
- Pokud galon barvy pokryje 250 čtverečních stop, kolik galonů barvy je potřeba k natření stodoly?
- Kartonová krabice je dokonalá krychle s hranou o rozměrech 17 palců. Kolik krychlových stop se do ní vejde?
- Bazén je 16 stop široký, 32 stop dlouhý a je rovnoměrně hluboký 4 stopy. Kolik krychlových stop vody se do něj vejde?
- Krabice od cereálií má délku 25 cm, šířku 9 cm a výšku 30 cm. Kolik cereálií se do ní vejde?
Odpovědi
Sítě a obvod:
- 40,5 palce2
- 838 cm2
- 252 čtverečních jednotek
- 1484.6 jednotek čtverečních
- 3990,7 cm3
Stodola:
- 2450 čtverečních stop
- 10 galonů barvy
- 2,85 cm3 (zde pozor. Jednotky v úloze jsou uvedeny v palcích, ale otázka požaduje stopy)
- 2048 krychlových stop
- 6750 cm3
Válec
Válec je trojrozměrný útvar s dvojicí rovnoběžných a shodných kruhových konců neboli podstav. Válec má jednu zakřivenou stranu, která při rovinném uspořádání tvoří obdélník.
Stejně jako u hranolů mohou být válce pravé nebo šikmé. Strana pravého válce je kolmá na jeho kruhové podstavy. Strana šikmého válce není kolmá na jeho podstavy.
Povrch válce pomocí sítí
Válec můžete rozložit na síť.
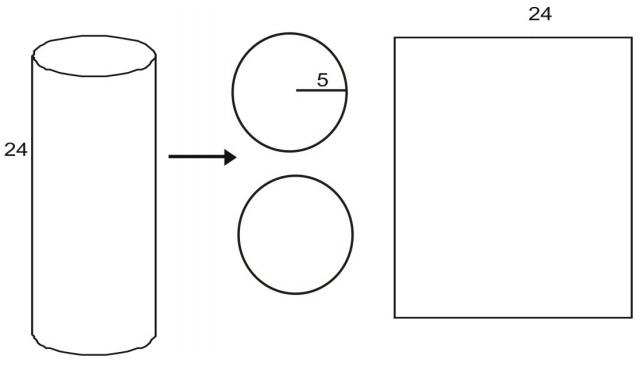
Plocha každé podstavy je dána plochou kružnice:
A=\pi{r}^2\
A=\pi(5)^2\
A=25\pi\
A\aprox(25)(3,14)=78,5\\
Plocha obdélníkové boční plochy L je dána součinem šířky a výšky. Výška je dána jako 24. Vidíte, že šířka plochy je rovna obvodu kruhové podstavy.
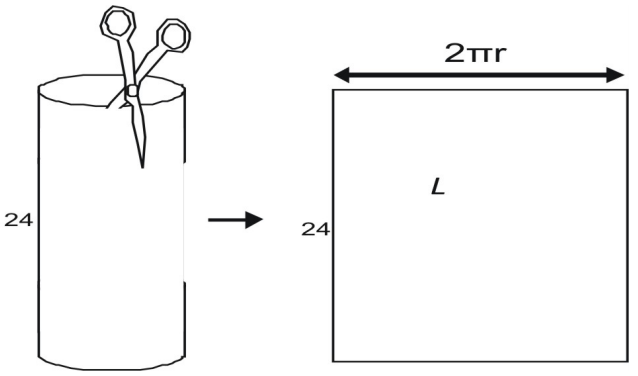
Pro zjištění šířky si představte, že nůžkami rozeberete válec podobný plechovce. Když rozstřihnete boční plochu, zjistíte, že je rovna obvodu vrcholu plechovky. Obvod kruhu je dán vztahem C = 2πr, boční plocha L je
L=2{\pi}rh\\
L=2{\pi}(5)(24)\\
L=240\pi\
L\aprox(240)(3.14)=753,6\\
Nyní můžeme zjistit plochu celého válce pomocí A = (plocha dvou podstav) + (plocha boční strany).
A=2(75,36)+753,6\\
A=904,32\\
Vidíte, že vzorec, který jsme použili k určení celkového povrchu, lze použít pro libovolný pravý válec.
Příklad 4
Při hledání plochy válce použijte síť.
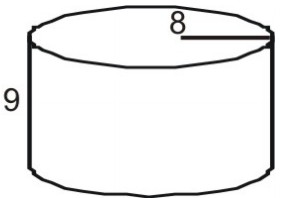
Nejprve nakreslete a označte síť pro obrázek.
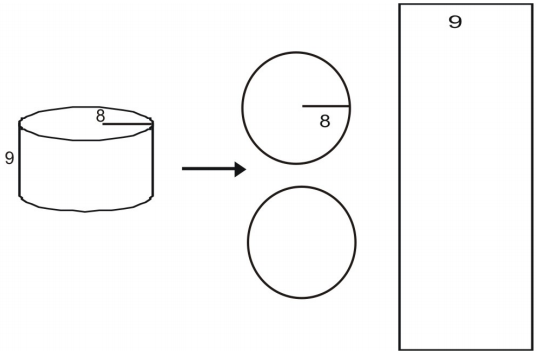
Vypočítejte plochu každé podstavy.
A=\pi{r}^2\\
A=\pi(8)^2\
A=64\pi\
A\aprox(64)(3.14)=200.96\\
Calculate L.
L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452,16\\
Zjistěte plochu celého válce.
A=2(200,96)+452,16\\
A=854.08\\
Celkový povrch je tedy přibližně 854,08 čtverečních jednotek
Povrch válce pomocí vzorce
Viděli jste, jak pomocí sítí zjistit celkový povrch válce. Postulát lze rozložit a vytvořit obecný vzorec pro všechny pravé válce.
A = 2B + L

Všimněte si, že základna B libovolného válce je: B = πr2
Boční plocha L pro libovolný válec je:
L=\text{šířka boční plochy}\cdot\text{výška válce}\\
L=\text{obvod podstavy}\cdot\text{výška válce}\\
L=2\pi{r}\cdot{h}\\
Složením obou rovnic dostaneme:
Složením a z rovnice získáme:
Povrch pravého válce: Plochu pravého válce o poloměru r a výšce h lze vyjádřit takto:
A = 2πr2 + 2πrh
nebo:
A = 2πr(r + h)
Součty lze použít k určení plochy libovolného pravého válce.
Příklad 5
Pomocí vzorce najděte povrch válce.
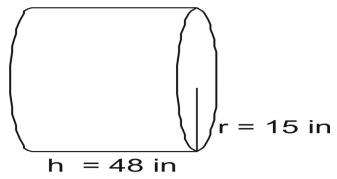
Napište vzorec, dosaďte hodnoty a vyřešte.
A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\text{ čtverečních palců}\\
Příklad 6
Zjistěte povrch válce.
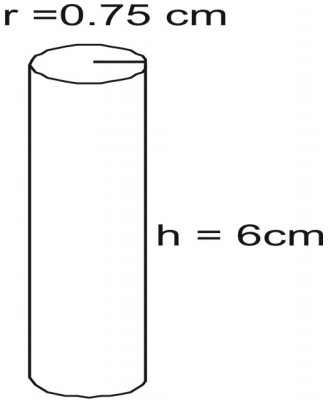
Napište vzorec, dosaďte do něj hodnoty a vyřešte.
A=2\pi{r}(r+h)\\
A=2(3,14)(0,75)\\
A=31. Jaký je povrch válce?7925\text{ čtverečních palců}\\
Příklad 7
Najděte výšku válce, který má poloměr 4 cm a povrch 226,08 cm2.
Napište vzorec s danými údaji a vyřešte h.
A=2\pi{r}(r+h)\\
226,08=2(3,14)(4)\\
226,08=25,12\\
226,08=100,48+25,12h\\
5=h\\
Koule
Koule je trojrozměrný útvar, který má tvar koule.

Sféry lze charakterizovat třemi způsoby.
- Sféra je množina všech bodů, které leží v pevné vzdálenosti r od jediného středového bodu O.
- Sféra je množina všech bodů, které leží v pevné vzdálenosti r od jediného středového bodu O.
- Koule je plocha, která vznikne po otočení kružnice kolem libovolného jejího průměru.
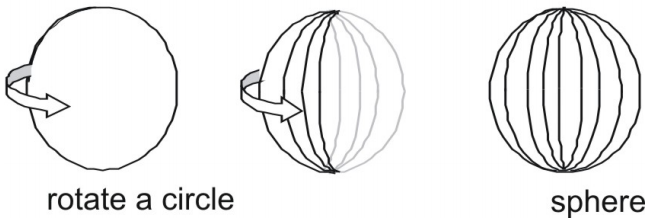
Povrch koule
Z měření koulí a válců lze odvodit vzorec pro povrch koule. Zde si ukážeme kouli o poloměru 3 a pravý válec o poloměru i výšce 3 a vyjádříme povrch ve tvaru π.
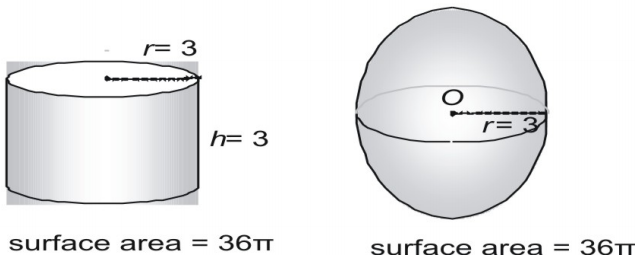
Nyní si vyzkoušíme větší dvojici a vyjádříme povrch v desetinném tvaru.
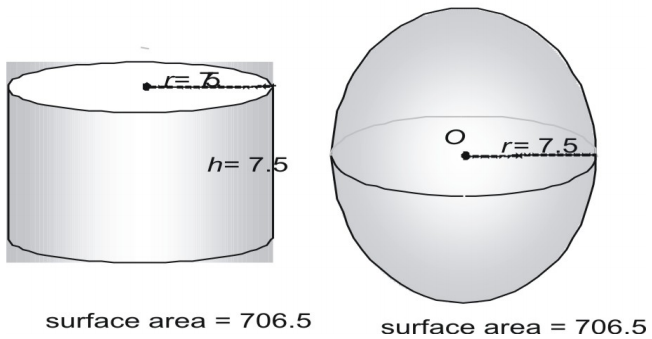
Podívejte se na třetí dvojici.
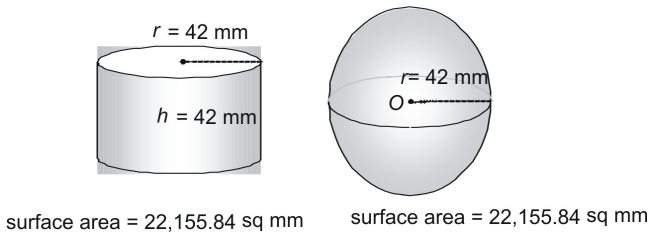
Je náhoda, že koule a válec, jejichž poloměr a výška se rovnají poloměru koule, mají úplně stejný povrch? Vůbec ne! Staří Řekové totiž používali metodu, která ukázala, že k nalezení povrchu libovolné koule (nebo jakéhokoli válce, v němž ) lze použít následující vzorec:
Plocha povrchu koule je dána vztahem: A = 4πr2Příklad 8
Najděte povrch koule o poloměru 14 stop.
Použijte vzorec.
A=4\pi{r}^2\
A=4\pi(14)^2\\
A=4\pi(196)\\
A=784\pi\
2461.76\text{ čtverečních stop s použitím }3,14\text{ pro }\pi\\Příklad 9
Zjistěte plochu následujícího obrázku ve vztahu π.
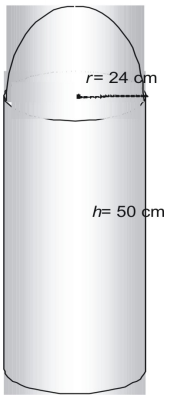
Útvar je tvořen jednou polokoulí nebo pologulí a jedním válcem bez vrcholu.
A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half koule})=2\pi(576)\\
A(\text{polovina koule})=1152\pi\text{ čtverečních cm}\Nyní zjistíme plochu válce bez jeho vrcholu.
A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\Thus, celkový povrch je 1152\pi+2976\pi=4128\pi\
Recenzní cvičení
- Zjistěte poloměr koule, která má objem 335 cm3.
- Určete povrch a objem tohoto útvaru:

- Poloměr koule je 4. Určete její objem a celkový povrch.
- Koule má poloměr 5. Určete její povrch a objem. Pravý válec, který má stejný poloměr, má stejný objem. Určete výšku a celkový povrch válce.
- Koule: objem = 296 cm3. Určete průměr.
- Sféra: povrch je 179 in2. Najděte poloměr.
- Tenisové míčky o průměru 3,5 palce se prodávají v plechovkách po třech kusech. Plechovka má tvar válce. Předpokládejme, že míčky se dotýkají plechovky po stranách, nahoře a dole. Jaký je objem prostoru, který nezabírají tenisové míčky?
- Koule má povrch 36π in2. Určete její objem.
- Obří naběračka ovládaná jeřábem má tvar polokoule o poloměru = 21 palců. Naběračka je naplněna roztavenou horkou ocelí. Když se ocel nalije do válcové zásobní nádrže, která má poloměr 28 palců, roztavená ocel vystoupá do výšky kolika palců?
Odpovědi
Poznamenej, že v těchto úlohách se nepoužívá číslo 3,14, ale číslo π.
- 1. Jakou výšku má roztavená ocel? Poloměr = 4,31 cm
- Povrch = 706,86 cm2
Objem = 1767,15 cm3 - Objem = 268,08 jednotek3
Povrch = 201,06 jednotek2 - Výška = 20/3 jednotek celkový povrch = 366,52 jednotek2
- Průměr = 8,27 cm
- Poloměr = 3.77 palců
- Objem válce = 32,16π in3 objem tenisových míčků = 21,44π in3
Objem prostoru, který nezabírají tenisové míčky = 33,68 in3 - Objem = 113,10 in3
- Výška roztavené oceli ve válci bude 7,88 in3
.



