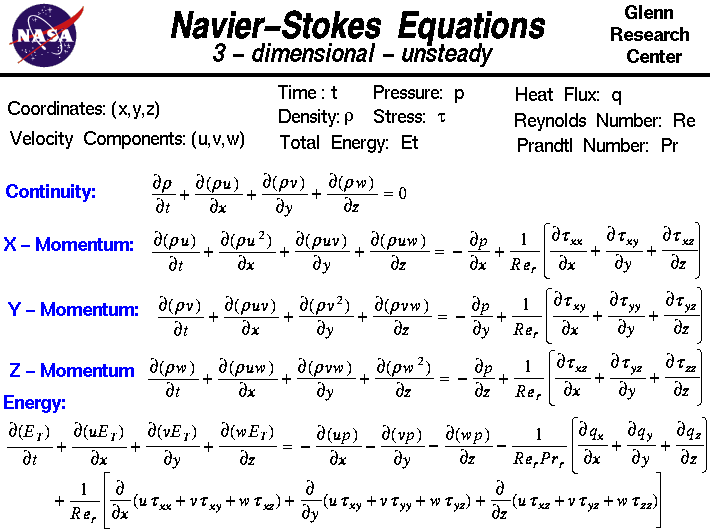
Na tomto slajdu si ukážeme trojrozměrný nestacionární tvar Navierových-Stokesových rovnic.Tyto rovnice popisují, jak spolu souvisí rychlost, tlak, teplota a hustota pohybující se kapaliny.Rovnice byly odvozeny nezávisle na sobě G.G. Stokesem v Anglii a M. Navier ve Francii na počátku 19. století.Rovnice jsou rozšířenímEulerových rovnic a zahrnují vliv viskozity na proudění.Tyto rovnice jsou velmi složité, přesto se je vysokoškolští studenti technických oborů učí odvozovat postupem velmi podobným odvození, které uvádíme na webové stránce o zachování hybnosti.
Rovnice jsou souborem spřažených diferenciálních rovnic a teoreticky by mohly být pro daný problém proudění řešeny pomocí metod z kalkulu. v praxi jsou však tyto rovnice příliš obtížné pro analytické řešení. v minulosti inženýři prováděli další aproximace a zjednodušení souboru rovnic, dokud nezískali skupinu rovnic, kterou mohli řešit. v poslední době se k řešení aproximací rovnic používají vysokorychlostní počítače pomocí různých technik, jako jsou metody konečných diferencí, konečných objemů, konečných prvků a spektrální metody.Tato oblast studia se nazývá výpočetní dynamika tekutin neboli CFD.
Navierovy-Stokesovy rovnice se skládají z časově závislé rovnice kontinuity pro zachování hmoty, tří časově závislých rovnic zachování momentu a časově závislé rovnice zachování energie.V problému jsou čtyři nezávislé proměnné, prostorové souřadnicex, y a z nějaké oblasti a čas t. Problém se řeší v závislosti na čase. Existuje šest závislých proměnných; tlak p, hustota r a teplota T (která je obsažena v energetické rovnici prostřednictvím celkové energie Et) a tři složky vektoru rychlosti; složka u je ve směru x, složka v je ve směru y a složka w je ve směru z. Všechny závislé proměnné jsou funkcemi všech čtyř nezávislých proměnných.Diferenciální rovnice jsou tedy parciální diferenciální rovnicea nikoliv obyčejné diferenciální rovnice, které studujete vpočátečních hodinách matematiky.
Všimněte si, že symbol diferenciálu je jiný než obvyklé „d /dt“ nebo „d /dx“, které vidíte u obyčejných diferenciálních rovnic. Symbol“
“ se používá k označení parciálních derivací. symbol naznačuje, že při výpočtu derivace máme držet všechny nezávislé proměnné pevně, kromě proměnné vedle symbolu. Soubor rovnic je následující:
Spojitost: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – hybnost: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – hybnost: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – hybnost: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energie: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
-. 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxy + v * tauyy + w * tauyz)/y tauxz + v * tauyz + w * tauzz)/z}
kde Re jeReynoldsovo číslo, což je parametr podobnosti, který je poměrem měřítka setrvačnosti proudění a viskózních sil v proudění. Proměnné q jsou složky tepelného toku a Pr je Prandtlovo číslo, což je parametr podobnosti, který je poměrem viskózních napětí k tepelným napětím. proměnné tau jsou složky tenzoru napětí. tenzor vznikne, když určitým způsobem vynásobíte dva vektory. Náš vektor rychlosti má tři složky; tenzor napětí má devět složek. Každá složka tenzoru napětí je sama o sobě druhou derivací složek rychlosti.
Výrazy na levé straně rovnic hybnosti se nazývají konvekční členy rovnic. konvekce je fyzikální proces, který probíhá v proudění plynu, při němž se přenáší nějaká vlastnost uspořádaným pohybem proudění.Difúze je fyzikální proces, ke kterému dochází při proudění plynu, kdy je nějaká vlastnost přenášena náhodným pohybem molekul plynu.Difúze souvisí s tenzorem napětí a viskozitou plynu. Turbulence a vznik mezních vrstev jsou výsledkem difúze v proudění.Eulerovy rovnice obsahují pouze konvekční členy Navierových-Stokesových rovnic, a proto nemohou modelovat mezní vrstvy. Existuje speciální zjednodušení Navierových-Stokesových rovnic, které popisují proudění v mezních vrstvách.
Všimněte si, že všechny závislé proměnné se objevují v každé rovnici. k vyřešení problému proudění je třeba vyřešit všech pět rovnic současně; to je důvod, proč tuto soustavu nazýváme spřaženou soustavou rovnic. ve skutečnosti existují ještě další rovnice, které jsou k řešení této soustavy nutné. Uvádíme pouze pět rovnic pro šest neznámých. Stavová rovnicevztahuje tlak, teplotu a hustotu plynu. a musíme určit všechny členy tenzoru napětí. v CFD se členy tenzoru napětí často aproximují pomocí turbulencemodelu.
Aktivity:
Průvodce
Navigace ..
Průvodce pro začátečníky Úvodní stránka