Free Press

Můj odhad je, že empirický vzorec kyseliny vinné již máte a že musíte zjistit její molekulový vzorec pomocí molární hmotnosti.

Předpokládám, že výchozím bodem je zde empirický vzorec kyseliny vinné, který vypadá takto

#“C“_2 „H“_3 „O“_3 -># empirický vzorec

Nyní vám empirický vzorec sloučeniny řekne nejmenší celočíselný poměr, který existuje mezi atomy jejích složek.

V tomto případě víte, že molekulový vzorec, který vám říká přesný počet atomů, které tvoří molekulu uvedené sloučeniny, bude obsahovat

#color(black)(„2 atomy C“ color(red)(“ pro každý „) {(„3 atomy H“),(„3 atomy O“) :}#

V podstatě hledáte násobek empirického vzorce.

Říká se, že molární hmotnost kyseliny vinné je #“150 g mol“^(-1)#. Vaším cílem zde bude určit molární hmotnost jejího empirického vzorce a poté tuto hodnotu použít k určení molekulového vzorce sloučeniny.

V tomto případě budete mít

#2 xx „12.

.011 g mol“^(-1) „“color(blue)(+)#
#3 xx „1,00794 g mol“^(-1)#
#3 xx „15,9994 g mol“^(-1)#
#color(white)(aaaaaaaaaaaaaaaaaaaa)/color(white)(aaaaaaaaaaaaaaaaaaaaaa)#
#“75.044 g mol“^(-1) -> #molární hmotnost empirického vzorce

Takže pokud má empirický vzorec molární hmotnost #“75.044 g mol“^(-1)# a molární hmotnost kyseliny vinné je #“150 g mol“^(-1)#, vyplývá z toho, že empirický vzorec musíte vynásobit

#(150 color(red)(cancel(color(black)(„g mol“^(-1)))))/(75.044color(red)(cancel(color(black)(„g mol“^(-1))))) = 1,999 ~~ color(red)(2)#

abyste získali molekulový vzorec. To znamená, že molekulový vzorec kyseliny vinné bude

#(„C“_2 „H“_3 „O“_3)_color(red)(2) znamená. color(green)(|bar(ul(color(white)(a/a) „C“_4 „H“_6 „O“_6color(white)(a/a)|)))#

Takto vypadá molekula kyseliny vinné

.
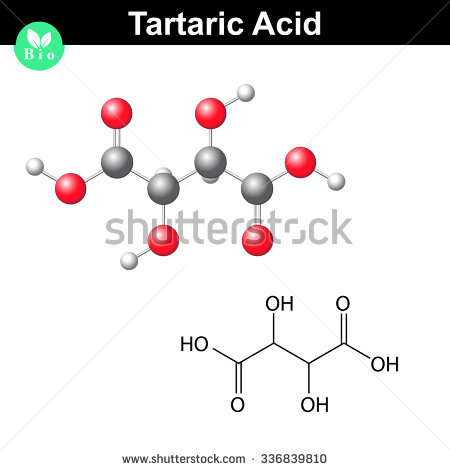