Sun, 18 Jun 2006
1+1=2
Whiteheadova a Russellova Principia Mathematica je proslulá tím, že dokázat, že 1+1=2, zabere tisíc stran. Samozřejmě dokazuje i spoustu dalších věcí. Kdyby chtěli dokázat pouze to, že 1+1=2, zabralo by to pravděpodobně jen polovinu místa.
Principia Mathematica je zvláštní kniha, která stojí za pozornost z historického i matematického hlediska. Byla napsána kolem roku 1910 a matematická logika byla tehdy ještě v plenkách, čerstvě po transformaci, na níž pracovali Peano a Frege. Zápis je poněkud nepřehledný, protože matematická notace se od té doby značně vyvinula. Podobně jako u špatně napsaného počítačového programu se v Principia Mathematica hodně opakuje kód, samostatné oddíly, které říkají v podstatě totéž, protože autoři se ještě nenaučili techniky, které by umožnily tyto oddíly spojit do jednoho.
Například oddíl ∗22, „Kalkul tříd“, začíná definicí relace podmnožiny (∗22.01) a operací sjednocení a průniku množin (∗22.02 a .03), doplňku množiny (∗22.04) a rozdílu dvou množin (∗22.05). Dále dokazuje komutativnost a asociativnost sjednocení a průniku množin (∗22.51, .52, .57 a .7), různé vlastnosti jako !!\alfa\cap\alfa = \alfa!!! (∗22.5) a podobně, až po věty jako ∗22.92: !!\alfa\podmnožina\beta \pravá šipka \alfa\cup(\beta -\alfa)!!.
Sekce ∗23 je „Kalkul relací“ a začíná téměř stejně, definováním relace podrelace (∗23.01) a operace relačního sjednocení a průniku (∗23.02 a .03), komplementu relace (∗23.04) a rozdílu dvou relací (∗23.05). Dále dokazuje komutativitu a asociativitu relačního sjednocení a průniku (∗23.51, .52, .57 a .7), různé vlastnosti jako !!\alfa\dot\cap\alfa = \alfa!!! (∗22.5) a podobně, až po věty jako ∗23.92: !!\alpha\dot\podmnožina\beta \pravá šipka \alpha\dot\cup(\beta \dot-\alpha)!!.
Kapitola ∗24 se zabývá existencí množin, nulové množiny !!\Lambda!!, univerzální množiny !!{\rm V}!!!, jejich vlastnostech a tak dále, a pak je oddíl ∗24 zdvojen v oddílu ∗25 v řadě tvrzení o existenci relací, nulové relaci !!\dot\Lambda!!!, univerzální relaci !!\dot {\rm V}!, jejich vlastnostech a tak dále.
Tak to udělali Whitehead a Russell v roce 1910. Jak bychom to udělali dnes? Relace mezi S a T je definována jako podmnožinaS × T, a je tedy množinou. Sjednocení, průnik, rozdíl a další operace jsou pro relace přesně stejné jako pro množiny, protože relace jsou množiny. Všechny věty o sjednoceních a průnicích relací, jako je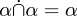 
, prostě zmizí, protože jsme je již dokázali pro množiny a relace jsou množiny. Nulovárelace je nulová množina. Univerzální relace je univerzální množina.
V roce 2006 odpadá obrovské množství dalších strojů, protože dochází ke sjednocení relací a množin. Principia Mathematica potřebuje speciální zápis a speciální definici pro výsledek omezení relace na ty dvojice, jejichž první prvek je členem určité množiny S, nebo jejichž druhý prvek je členem S, nebo jejichž oba prvky jsou členy S; v roce 2006 bychom prostě použili běžnou operaci průniku množin a mluvili o R ∩(S×B) nebo o čemkoli jiném.
Whitehead a Russell to v roce 1910 nemohli udělat, protože jim chyběl klíčový prvek: uspořádaná dvojice. V roce 1910 nikdo nevěděl, jaksestavit uspořádanou dvojici pouze z logiky a množin. V roce 2006 (nebo dokonce1956) bychom uspořádanou dvojici <a, b> definovali jako množinu {{a}, {a, b}}. Pak bychom pomocí vlastností množin ukázali jako větu, že <a, b> = <c, d> tehdy a jen tehdy, když a=c a b=d. Pak bychom definovali A×Bjako množinu všech p takových, že p = <a,b> ∧ a ∈ A ∧ b∈ B. Pak bychom definovali relaci na množináchA a B jako podmnožinu A×B. Pak bychom zdarma získali všechna ∗23 a ∗25 a spoustu ∗33 a ∗35 a ∗36 a pravděpodobně i spoustu dalších věcí.
(Mimochodem, to {{a}, {a, b}} vymyslel Kuratowski. Obvykle se připisuje Norbertu Wienerovi, aleWienerova myšlenka, ačkoli je podobná, byla ve skutečnosti složitější.“
V Principia Mathematica nejsou žádné uspořádané dvojice,leda implicitně. Dokonce tam nejsou téměř žádné množiny. Whitehead aRussell chtějí vše založit na logice. Pro Whiteheada a Russella je základním pojmem „výroková funkce“, což je funkce φ, jejímž výstupem je pravdivostní hodnota. Pro každou takovou funkci existuje odpovídající množina, kterou označují !!\hat x\phi(x)!!, množina všech xtak, že φ(x) je pravdivá. Pro Whiteheada a Russella je arelace implikována výrokovou funkcí dvou proměnných analogicky k tomu, jak je množina implikována výrokovou funkcí jedné proměnné. V roce 2006 se obejdeme bez „funkcí dvou proměnných“ a budeme hovořit pouze o funkcích, jejichž (jediným) argumentem je uspořádaná dvojice; relace se pak stane množinou všech uspořádaných dvojic, pro které je funkce pravdivá.
Russell údajně prohlásil, že objev Shefferova tahu (jediného logického operátoru, z něhož lze sestavit všechny ostatní logické operátory) je obrovským pokrokem a změní vše. To nám dnes připadá zvláštní, protože objev Shefferova tahu se zdá být tak jednoduchý a ve skutečnosti nic důležitého nemění. Stačí na začátek 1. kapitoly připojit poznámku, že ∼p a p∨q jsou zkratky pro p|p, respektive p|p.|.q|q, dokázat pět základních axiomů a vše ostatní nechat při starém. Russell však mohl s jistou dávkou spravedlnosti říci totéž o objevu, že uspořádané dvojice lze interpretovat jako množiny, což je jednoduchý objev, který by skutečně proměnil Principia Mathematica ve zcela jiné dílo.
V každém případě, s tímto pozadím na místě, můžeme diskutovat o důkazu 1+1=2 v Principia Mathematica. Ten se v Principia Mathematica objevuje poměrně pozdě, v oddíle ∗102. Moje zkrácená verze sahá pouze do ∗56, ale to je dost daleko na to, abychom se dostali k důležité předcházející větě, ∗54.43, naskenované níže:
Zápis může být zdrcující, takže se soustřeďme pouze na výrok věty, ignorujme vše ostatní, dokonce i užitečnoupoznámku dole:
Toto je věta, která se dokazuje; to, co následuje, je důkaz.
Teď bych měl vysvětlit zápis, který se od roku 1910 poněkud změnil. Za prvé, Principia Mathematica používala Peanův zápis „teček“ k rozklíčováníprecedence, kde nyní místo toho používáme závorky. Na tečkový zápis je třeba si zvyknout, ale oproti závorkám má některé zřetelné výhody. Podstata spočívá pouze v tom, že seskupení označujete vkládáním teček, takže (1+2)×(3+4)&krát(5+6) se zapisuje jako1+2.×.3+4.×.5+6. Prostřední podformule je mezi párem teček. Dílčí formule (1+2) je také mezi dvojicí teček, ale tečka na levém konci je nadbytečná a vynecháváme ji; podobně je dílčí formule (5+6) ohraničena tečkou vlevo a koncem formule vpravo.
Co když potřebujete vnořit závorky? Pak použijete více teček. Dvojitá tečka (:) je jako jednoduchá tečka, ale silnější. Například ((1+2)×3)+4 napíšeme jako 1+2 . ×3 : +4, přičemž dvojitá tečka oddělí celé 1+2 . × 3 do jednoduché podformule, na kterou se vztahuje +4.
Někdy potřebujete více úrovní precedence, a pak používáte trojtečky (.: a :.) a čtyřtečky (::). Tento vzorec, jak vidíte, mádvojité a trojité tečky. Převedeme-li tečky do standardního parentetického zápisu, dostaneme $$\ast54,43. \vdash ((\alfa, \beta \v 1 ) \supset (( \alfa\cap\beta = \Lambda) \equiv (\alfa\cup\beta \v 2)))$$. To vypadá poněkud nepřehledněji než verze s tečkami a u nekomplikovaných vzorců můžete mít potíže s určením, které parenteze odpovídají kterým. S tečkami je to vždy snadné. Proto si myslím, že je trochu nešťastné, že se tato konvence přestala používat.
Symbol !!\vdash!! se nezměnil; znamená, že formule, ke které se vztahuje, je tvrzena jako pravdivá. !!\supset!! je logická implikace a!!\equiv!! je logická ekvivalence. Λ je prázdná množina, kterou dnes zapisujeme jako ∅. ∩ ∪ a ∈ mají své modernívýznamy: ∩ a ∪ jsou operátory průniku a sjednocení množin a x∈y znamená, že x je prvkem množiny y.
Zbylé body jsou sémantické. α a β jsou množiny. 1označuje množinu všech množin, které mají právě jeden prvek. To znamená, že je to množina { c : existuje a takové, že c = {a } }. Mezi věty o 1 patří například:
- že Λ∉1 (∗52.21),
- že pokud α∈1, pak existuje nějaké x takové, že α ={x}. (∗52.1) a
- že {x}∈1 (∗52.22). Podobně
2 je množina všech množin, které mají přesně dva prvky. Důležitá věta o 2 je ∗54.3, která říká $$\ast54.3. \vdash 2 = \hat\alfa\{ (\existuje x) \> .\>x\in\alfa \> . \> \alfa – \iota`x\v 1 \}.$$V notaci Principia Mathematica se {x}, množina, která obsahuje x a nic jiného, zapisuje ι’x, takže tato věta říká, že 2 je totožná s množinou všech α takových, žeα má nějaký prvek x , který po odstranění z α ponechává jednoprvkovou množinu.
Tady je tedy opět věta ∗54.43:
Tvrdí, že mají-li množiny α a β každá právě jeden prvek, pak jsou disjunktní (tj. nemají žádné společné prvky) tehdy a jen tehdy, když jejich sjednocení má právě dva prvky.
Důkaz, který se objevuje ve výše uvedeném skenu za slovem „Dem.“ (zkratka pro „demonstraci“), vypadá takto:
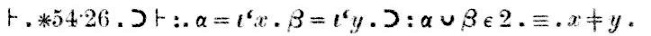
„Věta ∗54.26říká, že pokud α = {x} a β = {y}, pakα∪β má 2 prvky tehdy a jen tehdy, když x jeodlišné od y.“.
„Podle věty ∗51.231 je tento poslední kousek (x je různé ody) pravdivý tehdy a jen tehdy, když {x} a {y} jsoujednotlivé.“
„Podle věty ∗13.12 je tento poslední bit ({x} a {y} jsou disjunktní) pravdivý tehdy a jen tehdy, když α a β jsou samy disjunktní.“ Dílčí závěr v tomto bodě,který je označen (1), zní: jestliže α = {x} a β ={y}, pak α∪β ∈ 2 tehdy a jen tehdy, jestližeα∩β = Λ.
Důkaz pokračuje: „Ze závěru (1) spolu s tvrzeními ∗11.11 a ∗11.35 vyplývá, že pokud existují x a y tak, že α je{x} a β je {y}, pak α∪β ∈ 2 tehdy a jen tehdy, když α a β jsou disjunktní.“ Tento závěr je označen jako (2).
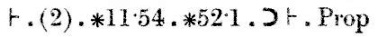
Závěr (2) spolu s větami ∗11.54 a ∗52.1 nakonec implikuje větu, kterou jsme se snažili dokázat.
Možná je třeba si všimnout, jak velmi malé jsou zde kroky.∗54.26, na němž tato věta silně závisí, je téměř stejný; tvrdí, že {x}∪{y} ∈ 2 tehdy a jen tehdy, když x≠y. ∗54.26 zase závisí na ∗54.101, který říká, že α má 2 prvky tehdy a jen tehdy, když existují x ay, které nejsou stejné, takové, že α = {x} ∪{y}. Věta ∗54.101 se jen nepatrně liší od definice 2. Věta ∗51.231 říká, že {x} a {y} jsou nesoudělné tehdy a jen tehdy, když x a y jsou různé. ∗52.1 je základní vlastností 1; viděli jsme ji již dříve.
Další věty citované v ukázce jsou velmi drobné technické záležitosti. ∗11.54 říká, že lze vzít tvrzení, že existují dvě věci, a rozdělit je na dvě tvrzení, z nichž každé tvrdí, že jedna z věcí existuje. ∗11.11 je ještě tenčí: říká, že pokud je φ(x, y) vždy pravdivé, pak můžete připojit univerzální kvantifikátor a tvrdit, že φ(x, y) je pravdivé pro všechna x a y. ∗13.12 se týká záměny rovných za rovné: jsou-li x a y stejné, pak x má vlastnost ψ tehdy a jen tehdy, když ji má i y.
Pozdější části Principia Mathematica jsem neviděl, protože můj výtisk končí za oddílem ∗56 a aritmetické věci jsou mnohem pozdější. Ale tato věta má jasně smysl 1+1=2 a pozdější věta (∗110.643), která skutečně tvrdí 1+1=2, na ní silně závisí.
Ačkoli si nejsem úplně jistý, co se stane později(už jsem nad tím ztratil příliš mnoho času, než abych věnoval další čas získání plné verze z knihovny), mohu si udělat kvalifikovaný odhad. Principia Mathematica bude definovat číslo 17 jako množinu všech 17prvkových množin a podobně jako každé jiné číslo; použití symbolu 2 pro množinu všech dvouprvkových množin to předznamenává. Množiny všech množin určité velikosti pak budou označovány jako „kardinální čísla“.
Principia Mathematica bude definovat součet kardinálních čísel p a qnějak takto: vezměme reprezentativní množinu a z p;a má p prvků. Vezměte reprezentativní množinu bz q;b má q prvků. Nechť c =a∪b. Je-li c členem nějakého kardinálníhočísla r a jsou-li a a b disjunktní, pak součet p a q je r.
Pomocí této definice lze dokázat obvyklé žádoucí vlastnosti sčítání, jako například x + 0 = x, x + y = y + x a 1 + 1 = 2. Pokud je c členem nějakého kardinálníhočísla, pak je c členem nějakého kardinálníhočísla r.
Zejména 1+1=2 vyplývá přímo z věty ∗54.43; je to přesně to, co chceme, protože k výpočtu 1+1 musíme najít dva nesouvislépředstavitele 1 a vzít jejich sjednocení; ∗54.43 tvrdí, že sjednocení musí být prvkem 2, bez ohledu na to, které představitele zvolíme, takže 1+1=2.
Post scriptum: Peter Norvig říká, že cirkumflex v notaciPrincipia Mathematica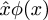 
je konečným zdrojem použití slovalambda pro označení anonymní funkce v programovacích jazycích Lisp a Python. Jistě víte, že tyto jazyky získaly slovo „lambda“ z použití řeckého písmene λ Alonzem Churchem pro vyjádření abstrakce funkce v jeho „λ-kalkulu“: V jazyce Lisp je(lambda (u) B) funkce, která přijímá argumentu a vrací hodnotu B; v λ-kalkulu je λu.B funkce, která přijímá argumentu a vrací hodnotu B. Norvig říká, že Church původně plánoval zapsat funkci λu.B jako û.B, ale jeho tiskárna neuměla psát s diakritikou. Uvažoval tedy, že cirkumflex přesune doleva a místo něj použije velkou lambdu:Λu.B. Velké Λ vypadalo příliš podobně jakoelogické a ∧, což bylo matoucí, a tak místo něj použil malou lambduλ.
Post post scriptum: Všichni vždycky říkají „Russell a Whitehead“. například výsledky vyhledávání v Googlu pro „Russell a Whitehead“ převyšují výsledky pro „Whitehead a Russell“ v poměru dvě ku jedné. Proč? Na obálce a titulní straně je napsáno „Alfred North Whitehead and Bertrand Russell,F.R.S.“. Jak a kdy Whitehead přišel o prvenství?
stálý odkaz
.