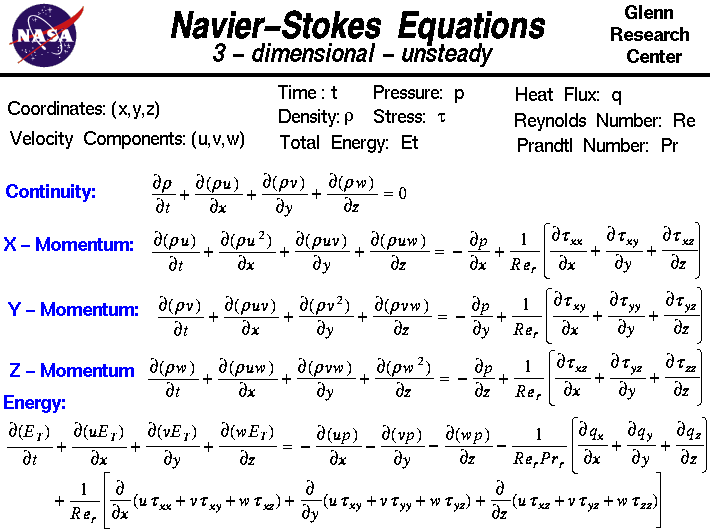
In questa diapositiva mostriamo la forma instabile tridimensionale delle equazioni di Navier-Stokes. Le equazioni sono estensioni delle equazioni di Eulero e includono gli effetti della viscosità sul flusso. Queste equazioni sono molto complesse, ma agli studenti universitari di ingegneria viene insegnato come ricavarle in un processo molto simile alla derivazione che presentiamo nella pagina web sulla conservazione della quantità di moto.
Le equazioni sono un insieme di equazioni differenziali accoppiate e potrebbero, in teoria, essere risolte per un dato problema di flusso usando i metodi del calcolo. Ma, in pratica, queste equazioni sono troppo difficili da risolvere analiticamente.Questa area di studio è chiamata Fluidodinamica computazionale o CFD.
Le equazioni di Navier-Stokes consistono in un’equazione di continuità dipendente dal tempo per la conservazione della massa, tre equazioni di conservazione del momento dipendenti dal tempo e un’equazione di conservazione dell’energia dipendente dal tempo.Ci sono quattro variabili indipendenti nel problema, le coordinate spaziali x, y e z di un dominio e il tempo t. Ci sono sei variabili dipendenti; la pressione p, la densità r e la temperatura T (che è contenuta nell’equazione dell’energia attraverso l’energia totale Et) e tre componenti del vettore velocità; la componente u è nella direzione x, la componente v è nella direzione y e la componente w è nella direzione z. Tutte le variabili dipendenti sono funzioni di tutte e quattro le variabili indipendenti.Le equazioni differenziali sono quindi equazioni differenziali parziali e non le equazioni differenziali ordinarie che si studiano in una classe di calcolo iniziale.
Si noterà che il simbolo differenziale è diverso dal solito “d /dt” o “d /dx” che si vede per le equazioni differenziali ordinarie. Il simbolo “
” è usato per indicare le derivate parziali; il simbolo indica che dobbiamo tenere fisse tutte le variabili indipendenti, tranne la variabile accanto al simbolo, quando calcoliamo una derivata. L’insieme delle equazioni sono:
Continuità: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momento: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Momento: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momento: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energia: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
dove Re è il numero di Reynolds che è un parametro di similarità che è il rapporto tra la scala dell’inerzia del flusso e le forze viscose nel flusso. Le variabili q sono le componenti del flusso di calore e Pr è il numero di Prandtl che è un parametro di somiglianza che è il rapporto tra le sollecitazioni viscose e le sollecitazioni termiche.Le variabili tau sono le componenti del tensore di stress.Un tensore si genera quando si moltiplicano due vettori in un certo modo. Il nostro vettore velocità ha tre componenti; il tensore di stress ha nove componenti. Ogni componente del tensore di sforzo è esso stesso una derivata seconda delle componenti della velocità.
I termini sul lato sinistro delle equazioni della quantità di moto sono chiamati i termini di convezione delle equazioni.La convezione è un processo fisico che si verifica in un flusso di gas in cui qualche proprietà è trasportata dal moto ordinato del flusso.I termini sul lato destro delle equazioni di quantità di moto che sono moltiplicati per l’inverso del numero di Reynolds sono chiamati termini di diffusione. La diffusione è un processo fisico che si verifica in un flusso di gas in cui qualche proprietà è trasportata dal movimento casuale delle molecole del gas, la diffusione è legata al tensore di stress e alla viscosità del gas. La turbolenza e la generazione di strati limite sono il risultato della diffusione nel flusso. Le equazioni di Eulero contengono solo i termini di convezione delle equazioni di Navier-Stokes e non possono, quindi, modellare gli strati limite. C’è una semplificazione speciale delle equazioni di Navier-Stok che descrivono i flussi degli strati limite.
Nota che tutte le variabili dipendenti appaiono in ogni equazione.Per risolvere un problema di flusso, devi risolvere tutte e cinque le equazioni simultaneamente; ecco perché chiamiamo questo un sistema accoppiato di equazioni.Ci sono in realtà alcune altre equazioni che sono necessarie per risolvere questo sistema. Mostriamo solo cinque equazioni per sei incognite. Un’equazione di stato lega la pressione, la temperatura e la densità del gas.E dobbiamo specificare tutti i termini del tensore di stress.In CFD i termini del tensore di stress sono spesso approssimati da un modello di turbolenza.
Attività:
Visite guidate
Navigazione ..
Guida per principianti Home Page