Amortized-analyysiä käytetään algoritmeissa, joissa on kalliita operaatioita, jotka tapahtuvat vain harvoin.

Amortized-analyysiä käytetään tavallisimmin tietorakenteiden kanssa, joissa on tilatiloja, jotka säilyvät operaatioiden välillä.Perusajatuksena on, että kallis operaatio voi muuttaa tilaa niin, että pahin tapaus ei voi toistua pitkään aikaan, jolloin sen kustannukset kuoletetaan.
Olkoon T1, T2, …, Tk tietorakenteeseen kohdistuvien operaatioiden sarjan monimutkaisuudet. Yksittäisen operaation kuoletettu monimutkaisuus tässä sekvenssissä on(T1 + T2 + …+ Tk) / k.
Esimerkki: dynaaminen matriisi
Dynaamisessa matriisissa elementit tallennetaan taustalla olevan kiinteän matriisin alkupäähän ja loput paikat ovat käyttämättömiä.
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Tässä on näkymä muistista, kun aluksi tyhjään matriisiin, jonka kapasiteetti on 2, liitetään elementit 2, 7, 1, 3, 8, 4.
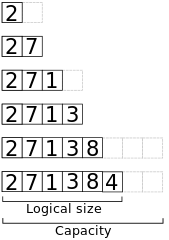
Pahimman tapauksen aika
Pahimman tapauksen aikakompleksisuus elementin liittämisessä matriisiin, jonka pituus on n, tätä algoritmia käyttäen on Θ(n).Jos matriisi on täynnä, algoritmi varaa uuden matriisin, jonka pituus on 2n,ja kopioi sen jälkeen elementit vanhasta matriisista uuteen matriisiin.
Varmasti tämä tulos on liian pessimistinen.Seuraavat n append-operaatiota ovat paljon halvempia -jokainen niistä suoritetaan vakioajassa, koska uudessa allokoidussa matriisissa on tilaa kaikille uusille elementeille.
Amortisoitunut aika
Amortisoituneen ajan analyysi antaa paljon paremman ymmärryksen algoritmista.
Harkitaan n append-operaation sekvenssiä,jossa aloitetaan matriisista, jonka pituus on 1. Huolellinen analyysi osoittaa,että näiden operaatioiden kokonaisaika on vain Θ(n).
- Vakioaikaisia osoitus- ja lisäysoperaatioita on yhteensä n.
- Koon muuttaminen tapahtuu vain operaatioilla 1, 2, 4, …, 2k, eli yhteensä 1 + 2 + 4 + …+ 2k = 2-2k-1 vakioaikaista elementin kopiointioperaatiota. Koska 2k ≤ n, tämä on korkeintaan 2n – 1.
Siten yhden lisäysoperaation jaksotettu aikakompleksisuus on Θ(1).
Lisää algoritmien analyysistä

Aikakompleksisuus: Laske askeleet

Suuri O-merkintä