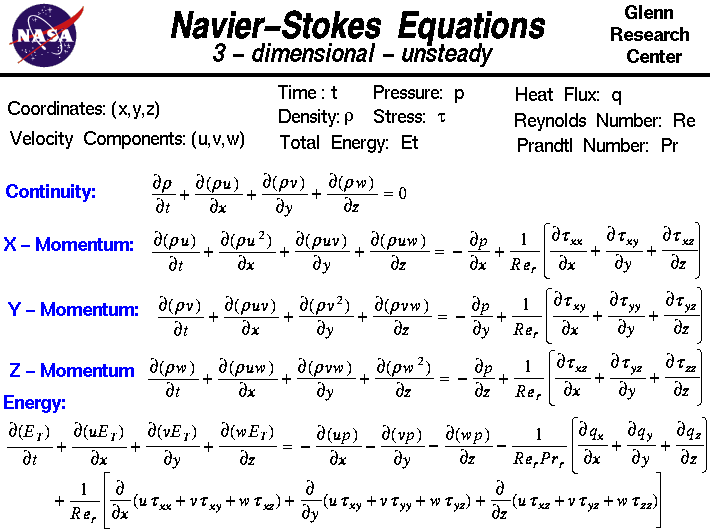
Tällä kalvolla näytämme Navier-Stokesin yhtälöiden kolmiulotteisen epävakaan muodon.Nämä yhtälöt kuvaavat, miten liikkuvan nesteen nopeus, paine, lämpötila ja tiheys liittyvät toisiinsa.Yhtälöt johdettiin toisistaan riippumatta G.G. Stokesin Englannissa ja M. Stokesin Englannissa. Yhtälöt ovat Eulerin yhtälöiden laajennuksia, ja ne sisältävät viskositeetin vaikutukset virtaukseen.Nämä yhtälöt ovat hyvin monimutkaisia, mutta insinööriopiskelijoille opetetaan niiden johtaminen hyvin samankaltaisella prosessilla kuin momentin säilyttämisen verkkosivulla esittelemämme derivointi.
Yhtälöt ovat joukko kytkettyjä differentiaaliyhtälöitä, ja ne voitaisiin teoriassa ratkaista tietylle virtausongelmalle käyttämällä laskennan menetelmiä.Käytännössä nämä yhtälöt ovat kuitenkin liian vaikeita ratkaistaviksi analyyttisesti.Aikaisemmin insinöörit tekivät lisää approksimaatioita ja yksinkertaistuksia yhtälökokonaisuuteen, kunnes heillä oli yhtälöryhmä, jonka he pystyivät ratkaisemaan.Viime aikoina suurnopeustietokoneita on käytetty ratkaisemaan approksimaatioita yhtälöihin käyttämällä erilaisia tekniikoita, kuten äärellinen differenssi-, äärellisen tilavuuden-, äärellisillä alkuaineilla tehtyjä analyysitapoja, ja spektrimenetelmiä.Tätä tutkimusaluetta kutsutaan nimellä Computational Fluid Dynamics tai CFD.
Navier-Stokesin yhtälöt koostuvat ajasta riippuvasta jatkuvuusyhtälöstä massan säilymiseksi, kolmesta ajasta riippuvasta momentin säilymisyhtälöstä ja ajasta riippuvasta energian säilymisyhtälöstä.Ongelmassa on neljä riippumatonta muuttujaa, joidenkin alueiden avaruuskoordinaatit x, y ja z sekä aika t. Nämä muuttujat eivät ole riippumattomia. Riippuvia muuttujia on kuusi; paine p, tiheys r ja lämpötila T (joka sisältyy energiayhtälöön kokonaisenergian Et kautta) sekä kolme nopeusvektorin komponenttia; u-komponentti on x-suunnassa, v-komponentti on y-suunnassa ja w-komponentti on z-suunnassa.Kaikki riippuvat muuttujat ovat kaikkien neljän riippumattoman muuttujan funktioita.Differentiaaliyhtälöt ovat siis osittaisdifferentiaaliyhtälöitäeikä tavallisia differentiaaliyhtälöitä, joita opiskelet alkeislaskutunnilla.
Huomaa, että differentiaaliyhtälön symboli eroaa tavallisista ”d /dt” tai ”d /dx”, joita näet tavallisissa differentiaaliyhtälöissä. Symbolia”
” käytetään osittaisderivaattojen merkitsemiseen.Symboli osoittaa, että meidän on pidettävä kaikki riippumattomat muuttujat kiinteinä lukuun ottamatta symbolin vieressä olevaa muuttujaa, kun laskemme derivaatan. Yhtälöryhmä on:
Jatkuvuus: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momentti: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Momentti: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momentti: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energia: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/(Re*Pr) * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxx + v * tauxy + w * tauyyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
jossa Re onReynoldsin luku,joka on samankaltaisuusparametri, joka on virtauksen inertiapainon skaalautumisen suhde virtauksen viskoosivoimiin. qmuuttujat ovat lämpövirran komponentteja ja Pr on Prandtlin luku,joka on samankaltaisuusparametri, joka on viskoosijännitysten suhde lämpöjännityksiin.tau-muuttujat ovat jännitystensorin komponentteja.Tensori syntyy, kun kaksi vektoria kerrotaan tietyllä tavalla. Nopeusvektorillamme on kolme komponenttia; jännitystensorilla onyhdeksän komponenttia. Jokainen jännitystensorin komponentti on itse nopeuskomponenttien toinen derivaatta.
Momenttiyhtälöiden vasemmalla puolella olevia termejä kutsutaan yhtälöiden konvektiotermiksi.Konvektio on fysikaalinen prosessi, joka tapahtuu kaasuvirtauksessa, jossa jokin ominaisuus siirtyy virtauksen järjestetyn liikkeen avulla.Impulssiyhtälöiden oikealla puolella olevia termejä, jotka kerrotaan käänteisellä Reynoldsin luvulla, kutsutaan diffuusiotermiksi.Diffuusio on fysikaalinen prosessi, joka tapahtuu kaasuvirtauksessa, jossa jokin ominaisuus siirtyy kaasun molekyylien satunnaisen liikkeen avulla.Diffuusio liittyy jännitystensoriin ja kaasun viskositeettiin. Turbulenssi ja rajakerrosten syntyminen ovat seurausta diffuusiosta virtauksessa.Eulerin yhtälöt sisältävät vain Navier-Stokesin yhtälöiden konvektiotermit, joten ne eivät voi mallintaa rajakerroksia. Navier-Stoken-yhtälöistä on olemassa erityinen yksinkertaistus, joka kuvaa rajakerrosvirtauksia.
Huomaa, että kaikki riippuvaiset muuttujat esiintyvät jokaisessa yhtälössä.Virtausongelman ratkaisemiseksi on ratkaistava kaikki viisi yhtälöä samanaikaisesti; siksi tätä kutsutaan kytketyksi yhtälösysteemiksi.Tämän systeemin ratkaisemiseen tarvitaan itse asiassa joitakin muita yhtälöitä. Esitämme vain viisi yhtälöä kuudelle tuntemattomalle. Tilayhtälö kertoo kaasun paineen, lämpötilan ja tiheyden.Ja meidän on määritettävä kaikki jännitystensorin termit.CFD:ssä jännitystensorin termejä approksimoidaan usein turbulenssimallilla.
Tehtävät:
Ohjattu kierros
Navigointi ..
Aloittelijan opas Etusivu