Rajakerros on liikkuvan virtauksen kanssa kosketuksissa olevan seinän kiinteän pinnan lähellä oleva ohut viskoosisen nesteen kerros, jossa (sen paksuuden δ sisällä) virtausnopeus vaihtelee nollasta seinän kohdalla (jossa virtaus ”tarttuu” seinään viskositeettinsa vuoksi) Ue:een rajalla, mikä vastaa suunnilleen (1 %:n virheen rajoissa) vapaan virtauksen nopeutta (ks. kuva 1). Tarkkaan ottaen δ:n arvo on mielivaltainen arvo, koska kitkavoima, joka riippuu nesteen ja kiinteän kappaleen välisestä molekyylivuorovaikutuksesta, pienenee etäisyyden kasvaessa seinämästä ja muuttuu nollaksi äärettömässä.
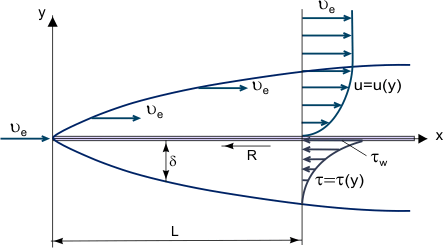
Kuva 1. Rajakerroksen kasvu tasaisella levyllä.
Rajakerroksen peruskäsitteen ehdotti L. Prandtl (1904), se määrittelee rajakerroksen nestekerrokseksi, joka kehittyy virtauksissa, joissa Reynoldsin luku Re on hyvin suuri, eli joissa viskositeetti on suhteellisen pieni verrattuna hitausvoimiin. Tämä havaitaan, kun kappaleet ovat alttiina suurille nopeuksille tai kun kappaleet ovat hyvin suuria ja ilmavirran nopeus on kohtalainen. Tällöin suhteellisen ohuessa rajakerroksessa kitkan leikkausjännitys (viskoosinen leikkausvoima): τ = η (jossa η on dynaaminen viskositeetti; u = u(y) – rajakerroksen pituussuuntaisen nopeuskomponentin ”profiili”, ks. kuva 1) voi olla hyvin suuri; erityisesti seinämässä, jossa u = 0 ja τw = ηw, vaikkakin viskositeetti itsessään voi olla melko pieni.
Voidaan jättää huomiotta rajakerroksen ulkopuoliset kitkavoimat (verrattuna hitausvoimiin) ja tarkastella Prandtlin käsitteen perusteella kahta virtausaluetta: rajakerrosta, jossa kitkavaikutukset ovat suuria, ja lähes invisidistä virtausydintä. Jos oletetaan, että rajakerros on hyvin ohut kerros (δ << L, missä L on sen kappaleen, jonka yli virtaus tapahtuu, tai virtauksen sisältävän kanavan tyypillinen lineaarinen ulottuvuus, jonka paksuus pienenee Re:n kasvaessa, kuva 1), voidaan rajakerroksen paksuuden suuruusluokkaa arvioida seuraavasta suhteesta:
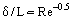
Esimerkiksi kun lentokone lentää nopeudella Ue = 400 km/h, rajakerroksen paksuus siiven takareunalla, jossa on 1 metrin sointu (profiilin pituus) on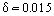 
m. Kuten kokeellisesti todettiin, rungon sisäänmeno-osaan kehittyy laminaarinen rajakerros. Vähitellen joidenkin epävakauttavien tekijöiden vaikutuksesta rajakerroksesta tulee epävakaa ja rajakerros siirtyy turbulenttisen virtauksen tilaan. Erityisissä kokeellisissa tutkimuksissa on todettu, että turbulentin ja laminaarisen alueen välillä on siirtymäalue. Joissakin tapauksissa (esimerkiksi ulkoisen virtauksen korkealla turbulenssitasolla) rajakerroksesta tulee turbulenttinen välittömästi virtauksen pysähtymispisteen alapuolella. Joissakin olosuhteissa, kuten voimakkaassa painehäviössä, kiihtyvissä turbulenttisissa virtauksissa tapahtuu käänteinen ilmiö, nimittäin virtauksen relaminarisoituminen.
Suhteellisesta ohuudestaan huolimatta rajakerros on hyvin tärkeä virtauksen ja kappaleen välisten dynaamisten vuorovaikutusprosessien käynnistämisen kannalta. Rajakerros määrittää lentävän ajoneuvon aerodynaamisen vastuksen ja nosteen tai kanavissa tapahtuvan nestevirtauksen energiahäviön (tässä tapauksessa hydrodynaaminen rajakerros, koska on olemassa myös terminen rajakerros, joka määrittää lämmönsiirron termodynaamisen vuorovaikutuksen).
Rajakerroksen parametrien laskeminen perustuu viskoosisen nesteen liikkeen Navier-Stokesin yhtälöistä saatujen yhtälöiden ratkaisemiseen, joita ensin yksinkertaistetaan huomattavasti ottaen huomioon rajakerroksen ohuus.
L. Prandtlin ehdottama ratkaisu on pohjimmiltaan Navier-Stokesin yhtälön potenssisarjojen laajenemisen ensimmäinen termi, ja sarjan laajeneminen suoritetaan dimensiottoman parametrin potensseille (δ/L). Pienempi parametri tässä termissä on nollapotenssissa, joten rajakerroksen yhtälö on rajakerroksen yhtälön (asymptoottisen ratkaisun) asymptoottisessa laajennuksessa (suurella Re:llä) nolla-approksimaatio.
Navier-Stokesin yhtälön muuntaminen rajakerroksen yhtälöksi voidaan osoittaa johtamalla Prandtlin yhtälö laminaariselle rajakerrokselle kaksiulotteisessa kokoonpuristumattomassa virtauksessa ilman kappaleen voimia.
Tällöin Navier-Stokesin yhtälöiden järjestelmä on:
Muutamien Yhtälön eräiden termien suuruusluokkien arvioimisen jälkeen. (2) ja pienten termien huomiotta jättämisen jälkeen laminaarisen rajakerroksen Prandtlin yhtälöiden järjestelmäksi tulee:
jossa x, y ovat pituussuuntaiset ja sivusuuntaiset koordinaatit (kuva 1); v on nopeuskomponentti ”y”-akselin suuntaisesti; p, paine; t, aika; ja n kinemaattinen viskositeetti.
Rajakerros on ohut, ja nopeus sen ulkoreunalla Ue voidaan määrittää riittävän tarkasti ja täsmällisesti ideaalisen (invisidisen) nestevirtauksen nopeutena seinää pitkin laskettuna ensimmäiseen approksimaatioon asti ottamatta huomioon rajakerroksen käänteistä vaikutusta ulkoiseen virtaukseen. Yhtälön (3) pituussuuntainen painegradientti = (pisteessä p(y) = const) voidaan kuvata ideaalisen nesteen Eulerin liikeyhtälön avulla. Edellä esitetyn perusteella Prandtlin yhtälöt äärellisessä muodossaan kirjoitetaan seuraavasti:
Tämä on toisen kertaluvun parabolisten, epälineaaristen osittaisdifferentiaaliyhtälöiden järjestelmä, joka ratkaistaan alku- ja reunaehtojen avulla
Yhtälösysteemi (4) kirjoitetaan nopeuskomponenttien u:n ja v:n aktuaalisille arvoille. Turbulenttiselle virtaukselle saatujen yhtälöiden yleistämiseksi on käytettävä turbulenttisen virtauksen parametrien todellisten, keskiarvoistettujen ja sykkivien komponenttien välistä tunnettua suhdetta. Esimerkiksi nopeuskomponenttien osalta on olemassa suhteet, jotka yhdistävät todelliset u- ja v-komponentit, keskimääräiset ū- ja 
komponentit sekä sykkivät u’ ja v’ -komponentit:
Joidenkin uudelleenjärjestelyjen jälkeen systeemistä (3) voidaan saada toinen yhtälösysteemi erityisesti tasaiselle virtaukselle:
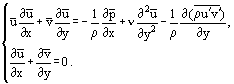
Käytetään seuraavaa suhdetta kitkaleikkausjännitykselle rajakerroksessa:
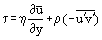
ja ottaen huomioon, että laminaarisessa rajakerroksessa u = u’ ja
on mahdollista kirjoittaa Prandtlin yhtälöt uudelleen muotoon, joka pätee sekä laminaariseen että turbulenttiseen virtaukseen:
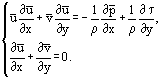
Yksinkertaisimmat ratkaisut on saatu laminaariselle rajakerrokselle ohuen litteän levyn päällä kaksiulotteisessa, samansuuntaisessa kokoonpuristumattoman nesteen virtauksessa (kuva 1). Tällöin yhtälöiden termien: x ~ L, y ~ δ, δ ~
suuruusluokan arviointi mahdollistaa muuttujien x ja y yhdistämisen yhdeksi relaatioksi
ja yhtälön (8) ratkaisun pelkistämisen (dp/dx = 0:n kohdalla dp/dx = 0) u:n ja v:n riippuvuuksien määrittämiseksi uudesta parametrista ξ. Toisaalta käyttämällä tunnettuja nopeuskomponenttien u, v ja virtausfunktion ψ
välisiä suhteita voidaan saada yksi kolmannen kertaluvun tavallinen epälineaarinen differentiaaliyhtälö, osittaisdifferentiaaliyhtälöiden järjestelmän (8)
Tässä f(ξ) on muuttujan ξ tuntematon funktio: f = ƒ =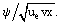
Yhtälön ensimmäinen numeerinen ratkaisu. (10) sai Blasius (1908) reunaehdoilla, jotka vastaavat rajakerroksen fysikaalisia olosuhteita kohdassa y = 0: u = 0, v = 0; kohdassa y → ∞; u → Ue (Blasiuksen rajakerros).
Kuviossa 2 verrataan Blasiuksen ratkaisun tuloksia (yhtenäinen viiva) kokeellisiin tietoihin. Näiden tietojen avulla voidaan arvioida viskoosin rajakerroksen paksuus. Kun ξ 
2,5, (u/Ue 0,99) (kuva 2); näin ollen yhtälöstä (9) saadaan:
Kuva 2.
Blasiuksen numeerisista laskelmista f(ξ)-funktion toisen derivaatan arvosta seinämän kitkaleikkausjännityksen kohdalla saadaan tässä tapauksessa yhteys:
Pituudeltaan L:n pituisen levyn (kuva 1) molemmin puolin vaikuttava kitkavoima R määräytyy niin ikään Yhtälöstä. (11):
kuten tasolevyjen kitkakerroin:
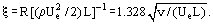
Huolimatta siitä, että Prandtlin yhtälöt ovat paljon yksinkertaisempia kuin Navier-Stokesin yhtälöt, niiden ratkaisut saatiin vain rajoitetulle määrälle ongelmia. Monissa käytännön ongelmissa ei ole tarpeen määrittää nopeusprofiileja rajakerroksessa, ainoastaan paksuus ja leikkausjännitys. Tällainen tieto voidaan saada ratkaisemalla integraalimomenttiyhtälö
Integraalisuhde (12) pätee sekä laminaariselle että turbulenttiselle rajakerrokselle.
Yhtälön (12) integraalin alapuolella ovat funktiot, joita ei tunneta a priori, mutta jotka luonnehtivat nesteen parametrien jakaantumista kerroksen paksuudella δ. Integraali on yhtälössä (12). Ja integraalin laskuvirhe on pienempi kuin likimääräisesti oletetun integraalifunktion ρu = ρu(y) virhe. Nämä luovat edellytykset kehittää likimääräisiä menetelmiä rajakerroksen parametrien laskemiseksi, jotka ovat vähemmän aikaa vieviä kuin tarkat Prandtlin yhtälöiden integrointimenetelmät. Peruskäsitteen ehdotti ensimmäisenä T. von Karman, joka otti käyttöön tällaisen mielivaltaisen kerrospaksuuden δ*
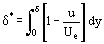
ja impulssin siirtymäpaksuuden δ**
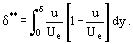
täten voimme muuntaa yhtälön yht. (12) kokoonpuristumattoman nesteen kaksiulotteiselle rajakerrokselle muotoon:
Yhtälössä (15) on kolme tuntematonta funktiota, nimittäin δ* = δ*(x), δ** = δ**(x) ja τw = τw(x) .
Yhtälön kaltaisen tavanomaisen differentiaaliyhtälön kuten Eq. (15) ratkaiseminen edellyttää yleensä oletusta (tai esitystä) nopeusjakaumasta (nopeusprofiilista) rajakerroksen paksuuden yli joidenkin ominaisparametrien (muotoparametrien) funktiona, ja se edellyttää myös empiiristen tietojen käyttöä kitkakertoimen Cf = 2τw/(ρU2e) ja rajakerroksen mielivaltaisen paksuuden välisestä suhteesta (kitkalaki).
Joitakin varmoja fysikaalisia selityksiä voidaan antaa δ*:n ja δ**:n arvojen osalta. Yhtälön (13) integraalifunktio sisältää uudelleenjärjestelyn jälkeen termin (Ue – u), joka luonnehtii nopeuden vähenemistä. Yhtälön (14) integraalia voidaan näin ollen pitää rajakerroksen läpi kulkevan virtausnopeuden pienenemisen mittana verrattuna täydelliseen nestevirtaukseen nopeudella Ue. Toisaalta δ*:n arvoa voidaan pitää kitkavoimien vaikutuksesta tapahtuvan ulkoisen virtaussuunnan poikkeaman mittana seinään nähden normaalia (y-akselia pitkin). Tästä yhtälön (14) integraalirakenteen tarkastelusta voidaan päätellä, että δ** luonnehtii momentin vähenemistä rajakerroksessa kitkan vaikutuksesta.
Seuraavat suhteet ovat voimassa:
jossa H on rajakerroksen nopeusprofiilin muotoparametri. Esimerkiksi lineaariselle jakaumalle u = ky,
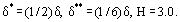
Tällä hetkellä turbulenttisen rajakerroksen parametrien ennustamiseen käytetään laajalti ns. puoliempiirisiä teorioita. Tällöin oletetaan, että kokonaiskitkajännitys τ turbulenttisessa rajakerroksessa on summa
Tässä τT on ylimääräinen (turbulenttinen tai Reynoldsin) kitkajännitys, erityisesti kokoonpuristumattomassa virtauksessa
katso Yht. (7).
Tämä esitys liittyy suoraan rajakerroksen liikeyhtälöiden järjestelmään (6). Kokoonpuristuvassa rajakerroksessa tiheyspulsaatioiden voidaan katsoa olevan seurausta lämpötilapulsaatioista
jossa β = (1/T) on tilavuuslaajenemiskerroin.
Tärinän τT määrittämiseen käytetään lisäksi turbulenttista impulssinsiirtoa koskevia puoliempiirisiä hypoteeseja. Esimerkiksi,
jossa ηT on J. Boussinesqin vuonna 1877 esittelemä turbulenttisen viskositeetin dynaaminen kerroin.
Molekulaarisen ja turbulenttisen vaihdon samankaltaisuuden käsitteen (samankaltaisuusteorian) pohjalta Prandtl esitti sekoittumispituushypoteesin (die Mischungsweg). Sekoittumispituus 1 on tie, jonka äärellinen nestetilavuus (”mooli”) kulkee keskimääräisen liikkeen kerroksesta toiseen muuttamatta momenttiaan. Tämän ehdon mukaisesti hän johti yhtälön, joka osoittautui perustavanlaatuiseksi rajakerrosteorian kannalta:
Turbulentilla alueella lähellä seinämää virtaavan rajakerroksen L. Prandtl piti pituutta 1 verrannollisena y
jossa κ on empiirinen vakio.
Lähellä seinämää, jossa ηT << η, viskoosinen molekyylikitka on määräävä tekijä. Tämän rajakerroksen osan δ1, jota kutsutaan laminaariseksi tai viskoosiseksi alakerrokseksi, paksuus on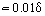 
. Alakerroksen ulkopuolella ηT:n arvo kasvaa ja on useita kertaluokkia suurempi kuin η. Vastaavasti tässä turbulenttiseksi ytimeksi kutsutussa rajakerroksen vyöhykkeessä τT > 0 = η. Joskus turbulenttinen ydin jaetaan puskurivyöhykkeeseen, jossa laminaarinen ja turbulenttinen kitka ovat vertailukelpoinen arvo, ja kehittyneeseen vyöhykkeeseen, jossa τT >> τ0. Tälle alueelle voidaan yhtälön (18) integroinnin ja yhtälön (19) huomioon ottamisen jälkeen johtaa lauseke logaritmiselle nopeusprofiilille:
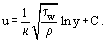
Jos käytetään dimensiottomia (tai universaalikoordinaatteja.
missä
on ns. dynaaminen nopeus (tai kitkanopeus), yht. (20) voidaan kirjoittaa uudelleen seuraavassa muodossa:
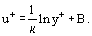
Nopeusjakauman esittämistä universaaleissa koordinaateissa ja turbulenttisen viskositeettikertoimen matemaattisia malleja käsitellään yksityiskohtaisemmin kohdassa Turbulenttinen virtaus.
Yksi nykyisistä versioista turbulenttisen rajakerroksen puoliempiirisestä teoriasta, jonka on kehittänyt S. S. Kutateladze ja A. I. Leontiev perustuu ns. turbulenttisten rajakerrosten asymptoottiseen teoriaan Re → ∞:ssä, jossa laminaarisen (viskoosisen) alakerroksen δ1 paksuus pienenee nopeammin kuin δ, minkä seurauksena (δ1/δ) → 0.
Tässä tilanteessa kehittyy turbulenttinen rajakerros, jonka viskositeetti on ”häviämässä”. Tässä kerroksessa η → 0, mutta se ei ole nolla, ja tältä osin kerros eroaa täydellisestä nestevirtauksesta. S. S. Kutateladzen ja A. I. Leontjevin (1990) esittämä suhteellisen kitkalain käsite osoittaa
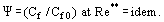
Laki määritellään tarkasteltavan olosuhteen kitkakertoimen Cf suhteena Cf0:n arvoon ”vakio-olosuhteissa” tasaisessa, läpäisemättömässä, kokoonpuristumattoman, isotermisen virtauksen ympäröimässä tasaisessa, läpäisemättömässä laatussa levyssä, ja kumpikin kitkakerroin on saatu, kun on pätevinä arvot: Re** = Ueδ**/ν. Osoitetaan, että kun Re → ∞; η → 0; ja Cf → 0, kitkakertoimen suhteellinen vaihtelu sellaisten häiriötekijöiden vaikutuksesta kuin painegradientti, kokoonpuristuvuus, epäisotermisyys, huokoisen seinämän läpi tapahtuva injektio (imu) jne. saa äärellisen arvon.
Yhtälöillä, jotka on johdettu Ψ:n arvon laskemista varten, on yksi tärkeä ominaisuus, joka tekee Ψ:stä riippumattoman turbulenssin empiirisistä vakioista. Integraalisen ”lähestymistavan” peruskäsitteen mukaisesti integraalimomenttiyhtälö muutetaan muotoon:
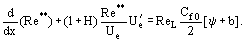
Tässä,
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) ovat läpäisevyysparametreja tilanteessa, jossa tiheydeltään ρw oleva kaasu injektoidaan läpäisevän seinämän lävitse nopeudella vw. Funktion Re** = Re**
määrittämiseksi on tarpeen laskea jakauma
Tässä tarkoituksessa sovelletaan häiriötekijöiden superpositioperiaatetta
Yhtälössä. 24 kukin kerroin edustaa suhteellista kitkalakia, jossa otetaan huomioon yhden tekijän vaikutus, muun muassa kokoonpuristuvuus ΨM, lämpötilan (tai entalpian) korkeus ΨT, injektio ΨB, painegradientti ΨP ja muut.
Rajakerroksen peruskäsitteet luovat edellytykset selittää sellaiset ilmiöt kuin virtauksen irtoaminen pinnasta virtauksen inertian vaikutuksesta, viskoosivirtauksen hidastuminen seinämästä ja vastavirtaan vaikuttava epäedullinen painegradientti = 0 tai < 0.
Jos painegradientti on epäsuotuisa pinnan kohdalla jaksojen ’1-4’ välissä (ks. kuva 3), nopeusjakauma u = u(x,y) rajakerroksessa muuttuu vähitellen; se muuttuu ”vähemmän täyteen”, pienentää kaltevuutta nestesuihkuissa, jotka ovat lähempänä seinämää ja joilla on vähemmän kineettistä energiaa (ks. nopeusprofiilin muodot kuvassa 3), jotka tunkeutuvat kauas virtaussuuntaan kohonneen paineen alueelle. Joissakin jaksoissa, esimerkiksi jaksossa ”4”, virtaviivalla ”a-a” (katkoviiva kuvassa 3) olevat nestehiukkaset – jotka ovat täysin kuluttaneet kineettisen energiansa loppuun – hidastuvat (ua = 0).
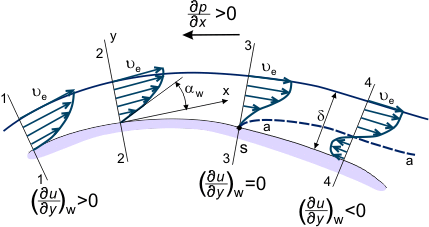
Kuva 3. Nestehiukkaset, jotka ovat virtaviivalla ”a-a” (katkoviiva kuvassa 3). Rajakerros virtauksessa peitetyn pinnan yli.
Staattinen paine ja painegradientin arvo eivät vaihtele rajakerroksen paksuuden mukaan. Tämän vuoksi nestehiukkaset, jotka ovat lähempänä seinää kuin linja ”a-a” ja joilla on vielä vähemmän energiaa, alkavat liikkua vastakkaiseen suuntaan painegradientin vaikutuksesta kohdassa ”4-4” (ks. kuva 3). Näin ollen suhde:
Tällä tavoin joissakin pinnan kohdissa nopeusprofiili muuttuu. Tälle muutokselle on ominaista derivaatan w merkin muuttuminen positiivisesta (kohta 2, kuva 3) negatiiviseksi (kohta 4). On tietenkin mahdollista määritellä myös jakso, jossa w = 0 (jakso 3, kuva 3). Tätä kutsutaan rajakerroksen erottumisjaksoksi (vastaavasti piste ”S” tämän jakson pinnalla on erottumispiste). Sille on ominaista käänteisen virtausvyöhykkeen kehittyminen – virtaus kappaleen ympärillä ei ole enää tasaista, rajakerros paksuuntuu huomattavasti ja ulkoisen virtauksen virtaviivat poikkeavat kappaleen ympärillä lentävän kappaleen pinnasta. Erotuskohdan alapuolella staattinen painejakauma kerroksen paksuuden yli ei ole tasainen eikä staattinen painejakauma pintaa pitkin vastaa ulkoisen, invisidisen virtauksen painejakaumaa.
Erottumista seuraa käänteisen virtauksen vyöhykkeiden ja pyörteiden kehittyminen, joissa ulkoisesta virtauksesta syötetty liike-energia muuttuu lämmöksi kitkavoimien vaikutuksesta. Virtauksen erottuminen, johon liittyy energian häviäminen vastavirtauksen pyörrevyöhykkeissä, johtaa sellaisiin ei-toivottuihin vaikutuksiin kuin lentävien ajoneuvojen ilmanvastuksen lisääntyminen tai hydrauliset häviöt kanavissa.
Toisaalta eroteltuja virtauksia käytetään erilaisissa laitteissa nesteen intensiiviseen sekoittamiseen (esimerkiksi polttoaineen ja ilman sekoittumisen parantamiseksi moottoreiden polttokammioissa). Kun viskoosit nesteet virtaavat kanavissa, joiden poikkileikkaus on muuttuva (vaihteleva painegradientti), erotteluvyöhyke voi olla paikallinen, jos diffuusoriosuutta seuraa sekoittajaosuus, jossa erotettu virtaus kiinnittyy jälleen pintaan (ks. kuva 4a). Kun virtaus irtoaa kappaleen takareunasta (esimerkiksi siiven takareunasta), muodostuu niin sanottu vanavedenkehä, joka muodostuu ”linkittyvistä” rajakerroksista (ks. kuva 4b).
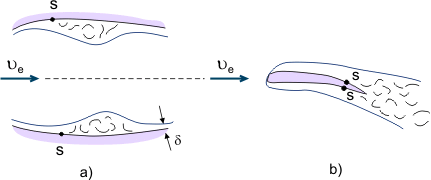
Kuva 4. Virtaus irtoaa kappaleen takareunasta. Rajakerroksen erotusilmiöt.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. ja Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers (Lämmönsiirto, aineensiirto ja turbulentit rajakerrokset), Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.