Sun, 18 Jun 2006
1+1=2
Whiteheadin ja Russellin Principia Mathematica -teos on kuuluisa siitä, että se vie tuhat sivua todistaakseen, että 1+1=2. Toki siinä todistetaan paljon muutakin. Jos he olisivat halunneet todistaa vain, että 1+1=2, se olisi luultavasti vienyt vain puolet vähemmän tilaa.
Principia Mathematica on outo kirja, johon kannattaa perehtyä sekä historiallisesta että matemaattisesta näkökulmasta. Se on kirjoitettu noin vuonna 1910, ja matemaattinen logiikka oli tuolloin vielä lapsenkengissään, tuoreena Peanon ja Fregen siihen tekemästä muutoksesta. Merkintätapa on hieman epäselvä, koska matemaattinen merkintätapa on kehittynyt huomattavasti sen jälkeen. Monet yksinkertaiset tekniikat, joita pidämme nykyään itsestäänselvyyksinä, puuttuvat.Kuten huonosti kirjoitettu tietokoneohjelma, suuri osa Principia Mathematican sisällöstä on toistokoodia, erillisiä osioita, joissa sanotaan pohjimmiltaan samat asiat, koska kirjoittajat eivät ole vielä oppineet tekniikoita, jotka mahdollistaisivat näiden osioiden yhdistämisen yhdeksi kokonaisuudeksi.
Esimerkiksi jakso ∗22, ”Luokkien laskenta”, alkaa määrittelemällä osajoukkojen relaation (∗22.01), joukkojen yhdistämisen ja leikkaamisen operaatiot (∗22.02 ja .03), joukon komplementin (∗22.04) ja kahden joukon erotuksen (∗22.05). Sitten todistetaan joukkojen yhdistämisen ja leikkaamisen kommutatiivisuus ja assosiatiivisuus (∗22.51, .52, .57 ja .7), erilaiset ominaisuudet, kuten !!\alpha\cap\alpha = \alpha!!! (∗22.5) ja sen kaltaiset, aina lauseisiin kuten ∗22.92: !!\alpha\subset\beta \rightarrow \alpha\cup(\beta -\alpha)!!.
Jakso ∗23 on ”Suhdelaskenta”, ja se alkaa melkeinpä täsmälleen samalla tavalla määrittelemällä alisuhderelaatio (∗23.01) sekä relaatioiden yhdistämisen ja leikkaamisen operaatiot (∗23.02 ja .03), relaation komplementti (∗23.04) ja kahden relaation erotus (∗23.05). Myöhemmin todistetaan relaatioiden yhdistämisen ja leikkaamisen kommutatiivisuus ja assosiatiivisuus (∗23.51, .52, .57 ja .7), erilaiset ominaisuudet, kuten !!\alpha\dot\cap\alpha = \alpha!!! (∗22.5) ja vastaavat, aina lauseisiin kuten ∗23.92: !!\alpha\dot\subset\beta \rightarrow \alpha\dot\cup(\beta \dot-\alpha)!!.
Luvussa ∗24 käsitellään joukkojen olemassaoloa, nollajoukkoa !!\Lambda!!, universaalijoukkoa !!{\rm V}!!!, niiden ominaisuuksista ja niin edelleen, ja sittenjakso ∗24 toistetaan jaksossa ∗25 sarjana teoreemoja relaatioiden olemassaolosta, nollarelaatiosta !!\dot\Lambda!!, universaalista relaatiosta !!\dot {\rm V}!!,niiden ominaisuuksista ja niin edelleen.
Siten Whitehead ja Russell tekivät sen vuonna 1910. Miten me tekisimme sen nykyään? S:n ja T:n välinen relaatio määritellään S × T:n osajoukoksi ja on siten joukko. Unioni, leikkaus, ero ja muut operaatiot ovat relaatioille täsmälleen samat kuin joukoille, koska relaatiot ovat joukkoja. Kaikki relaatioiden yhtymiä ja leikkauksia koskevat lauseet, kuten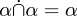 
, katoavat, koska todistimme ne jo joukoille ja relaatiot ovat joukkoja. Nollarelaatio on nollajoukko. Universaali relaatio on universaali joukko.
Vuonna 2006 häviää valtava määrä muita koneita, koska relaatioiden ja joukkojen yhdistäminen on tehty. Principia Mathematica tarvitsee erikoisnimityksen ja erikoismääritelmän tulokselle, joka saadaan rajoittamalla relaatio niihin pareihin, joiden ensimmäinen elementti on tietyn joukon S jäsen, tai joiden toinen elementti on S:n jäsen, tai joiden molemmat elementit ovat S:n jäseniä; vuonna 2006 käytettäisiin vain tavallista joukkojen leikkausoperaatiota ja puhuttaisiin R ∩(S×B):stä tai mistä tahansa.
Whitehead ja Russell eivät voineet tehdä tätä vuonna 1910, koska ratkaiseva osa koneistosta puuttui: järjestetty pari. Vuonna 1910 kukaan ei osannut rakentaa järjestettyä paria pelkän logiikan ja joukkojen avulla. Vuonna 2006 (tai jopa vuonna 1956) määrittelisimme järjestetyn parin <a, b> joukoksi {{a}, {a, b}}. Sitten osoittaisimme teoreemana, että <a, b> = <c, d>jos ja vain jos a=c ja b=d, käyttäen joukkojen ominaisuuksia. Sitten määrittelisimme A×B kaikkien sellaisten p:iden joukoksi, jotka ovat sellaisia, että p = <a,b> ∧ a ∈ A ∧ b∈ B. Sitten määrittelisimme joukkojenA ja B suhteen A×B:n osajoukoksi. Silloin saisimme kaikki ∗23 ja ∗25 ja paljon ∗33 ja ∗35 ja ∗36 ilmaiseksi, ja luultavasti paljon muutakin.
(Muuten, {{a}, {a, b}}-juttu on Kuratowskin keksimä.). Se liitetään yleensä Norbert Wieneriin, mutta Wienerin idea, vaikkakin samankaltainen, oli itse asiassa monimutkaisempi.)
Principia Mathematicassa ei ole järjestettyjä pareja,paitsi implisiittisesti. Joukkoja ei juurikaan edes ole. Whitehead jaRussell haluavat perustaa kaiken logiikkaan. Whiteheadille ja Russellille perustavanlaatuinen käsite on ”propositionaalinen funktio”, joka on funktio φ, jonka tulos on totuusarvo. Jokaiselle tällaiselle funktiolle on olemassa vastaava joukko, jota he merkitsevät !!\hat x\phi(x)!!!, kaikkien sellaisten x:ien joukko, joiden φ(x) on tosi. Whiteheadille ja Russellille kahden muuttujan propositionaalinen funktio merkitsee arelaatiota, samoin kuin yhden muuttujan propositionaalinen funktio merkitsee joukkoa. Vuonna 2006 luovumme ”kahden muuttujan funktioista” ja puhumme vain funktioista, joiden (yksi) argumentti on järjestetty pari; relaatiosta tulee tällöin kaikkien niiden järjestettyjen parien joukko, joiden suhteen funktio on tosi.
Russellin kerrotaan sanoneen, että Sheffin iskun (yksi looginen operaattori, josta kaikki muut loogiset operaattorit voidaan rakentaa) keksiminen oli valtava edistysaskel ja muuttaisi kaiken. Tämä tuntuu meistä nyt oudolta, koska Shefferin iskun löytäminen vaikuttaa niin yksinkertaiselta, eikä se oikeastaan muuta mitään tärkeää. Luvun 1 alkuun on vain lisättävä huomautus, jossa sanotaan, että ∼p ja p∨q ovat lyhenteitä p|p:lle ja p|p.|.q|q:lle, todistetaan viisi perusaksioomaa ja jätetään kaikki muu ennalleen. Mutta Russell olisi saattanut oikeutetusti sanoa samaa siitä havainnosta, että järjestetyt parit voidaan tulkita joukoiksi, yksinkertaisesta havainnosta, joka todella olisi muuttanut Principia Mathematican aivan toisenlaiseksi teokseksi.
Joka tapauksessa, kun tämä tausta on kunnossa, voimme keskustella Principia Mathematican todistuksesta 1+1=2. Tämä tapahtuu Principia Mathematican loppupuolella, kohdassa ∗102. Lyhennetty versioni ulottuu vain ∗56:een, mutta se riittää riittävän pitkälle, jotta pääsemme tärkeään edeltävään lauseeseen, ∗54.43, joka on skannattu alla:
Notaatio voi olla ylivoimaista, joten keskitytään vain lauseen lausumaan ja jätetään kaikki muu huomiotta, jopa alareunassa oleva hyödyllinen huomautus:
Tämä on lause, joka todistetaan; mitä seuraa, on todistus.
Nyt minun pitäisi selittää merkintätapa, joka on muuttunut jonkin verran vuodesta1910. Ensinnäkin Principia Mathematica käyttää Peanon ”pisteiden” merkintätapaa etusijan erottamiseksi, kun me nyt käytämme sen sijaan sulkuja. Pistemerkintä vaatii totuttelua, mutta sillä on joitakin selviä etuja sulkeisiin verrattuna. Ideana on vain se, että ryhmittely ilmaistaan laittamalla pisteitä, joten (1+2)×(3+4)×(5+6) kirjoitetaan seuraavasti: 1+2.×.3+4.×.5+6. Keskimmäinen alakaava on pisteiden välissä. Alakaava (1+2) on myös pisteparin välissä, mutta vasemmanpuoleinen piste on tarpeeton ja jätetään pois; samoin alakaava (5+6) on rajattu vasemmalla puolella pisteellä ja oikealla puolella kaavan lopulla.
Mitä, jos sulkeissa on oltava pesä? Silloin käytetään enemmän pisteitä. Kaksoispiste (:) on kuin yksittäinen piste, mutta vahvempi. Esimerkiksi kirjoitetaan ((1+2)×3)+4 muodossa 1+2 . × 3 : + 4, ja tuplapiste erottaa koko 1+2 . × 3 -lausekkeen yksittäiseksi alakaavaksi, johon +4 pätee.
Joskus tarvitaan useampia etuoikeustasoja, ja silloin käytetään kolmoispisteitä (.: ja :.) ja nelipisteitä (::). Tässä kaavassa, kuten näet, on kaksoispisteitä ja kolmoispisteitä. Kääntämällä pisteet tavalliseen parenteesin merkintätapaan saadaan $$$\ast54.43. \vdash ((\alpha, \beta \in 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \in 2)))$$. Tämä on melko sekavamman näköinen kuin versio, jossa on pisteitä, ja monimutkaisissa kaavoissa voi olla vaikeuksia selvittää, mitkä sulut sopivat mihinkin. Pisteiden kanssa se on aina helppoa. Joten minusta on hieman valitettavaa, että tämä konventio on jäänyt pois käytöstä.
Symboli !!\vdash!! ei ole muuttunut; se tarkoittaa, että kaavan, johon sitä sovelletaan, väitetään olevan tosi. !!\supset!! on looginen implikaatio, ja!!\equiv!! on looginen ekvivalenssi. Λ on tyhjä joukko, joka kirjoitetaan nykyään ∅. ∩ ∪ ja ∈ ovat nykymerkityksiä: ∩ ja ∪ ovat joukkojen leikkaus- ja yhdistämisoperaattoreita, ja x∈y tarkoittaa, että x on joukon y elementti.
Loput kohdat ovat semanttisia. α ja β ovat joukkoja. 1merkitsee kaikkien niiden joukkojen joukkoa, joilla on täsmälleen yksi alkio. Eli se on joukko { c : on olemassa a siten, että c = {a } }. 1:tä koskevia teoreemoja ovat esimerkiksi:
- että Λ∉1 (∗52.21),
- että jos α∈1 niin on olemassa jokin x siten, että α ={x} (∗52.1), ja
- että {x}∈1 (∗52.22).
2 on vastaavasti kaikkien niiden joukkojen joukko, joilla on täsmälleen kaksi alkiota. Tärkeä 2:ta koskeva lause on ∗54.3, joka sanoo $$$\ast54.3. \vdash 2 = \hat\alpha\{ (\on olemassa x) \> .\>x\in\alpha \> . \> \alpha – \iota`x\in 1 \}.$$$Principia Mathematican merkinnöissä {x}, joukko, joka sisältää x:n eikä mitään muuta, kirjoitetaan ι’x, joten lause sanoo, että 2 on identtinen kaikkien sellaisten α:iden joukon kanssa, joissaα:lla on jokin alkio x , joka poistettaessa α:sta jäljelle jää 1-alkioinen joukko.
Tässä on siis taas lause ∗54.43:
Se väittää, että jos joukoilla α ja β on kummallakin täsmälleen yksi alkio, niin ne ovat disjointteja (eli niillä ei ole yhtään yhteistä alkiota), jos ja vain jos niiden liitoksessa on täsmälleen kaksi alkiota.
Todistus, joka esiintyy yllä olevassa skannauksessa sanan ”Dem.” (lyhenne sanasta ”demonstration”) jälkeen, menee näin:
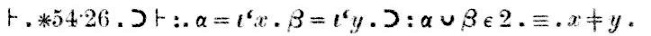
”Theorem ∗54.26esittää, että jos α = {x} ja β = {y}, niinα∪β:llä on 2 alkiota, jos ja vain jos x on erilainen kuin y.”.
”Lauseen ∗51.231 mukaan tämä viimeinen osa (x on erilainen kuiny) on tosi, jos ja vain jos {x} ja {y} ovatdisjoint.”
”Periaatteen ∗13.12 mukaan tämä viimeinen bitti ({x} ja {y} ovat erillisiä) ontosi, jos ja vain jos α ja β ovat erillisiä.” Osittainen johtopäätös tässä kohdassa,joka on merkitty (1), on, että jos α = {x} ja β ={y}, niin α∪β ∈ 2 jos ja vain josα∩β = Λ.
Todistus jatkuu: ”Johtopäätös (1) yhdessä lauseiden ∗11.11 ja ∗11.35 kanssa merkitsee, että jos on olemassa x ja y siten, että α on{x} ja β on {y}, niin α∪β ∈ 2jos ja vain jos α ja β ovat disjointteja.”. Tämä johtopäätös on merkitty merkinnällä (2).
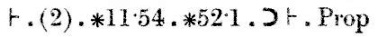
Loppujen lopuksi johtopäätös (2) yhdessä lauseiden ∗11.54 ja ∗52.1 kanssa implikoi lauseen, jota yritimme todistaa.
Mahdollisesti huomattavaa tässä on se, kuinka hyvin pieniä askeleet ovat.∗54.26, josta tämä lause riippuu voimakkaasti, on lähes sama; se väittää, että {x}∪{y} ∈ 2 jos ja vain jos x≠y. ∗54.26 puolestaan riippuu ∗54.101:stä, jonka mukaan α:lla on 2 alkiota, jos ja vain jos on olemassa x jay, jotka eivät ole samat, niin että α = {x} ∪{y}. Lause ∗54.101 eroaa vain vähän 2:n määritelmästä. Lause ∗51.231 sanoo, että {x} ja {y} ovat disjointteja, jos ja vain jos x ja y ovat erilaisia. ∗52.1 on 1:n perusominaisuus; näimme sen jo aiemmin.
Muut demonstraatiossa mainitut lauseet ovat hyvin pieniä teknisiä asioita. ∗11.54 sanoo, että voidaan ottaa väite, että kaksi asiaa on olemassa, ja jakaa se kahdeksi väitteeksi, joista kumpikin väittää, että toinen asioista on olemassa. ∗11.11 on vieläkin ohuempi: siinä sanotaan, että jos φ(x, y) on aina tosi, siihen voidaan liittää yleispätevä kvanttori ja väittää, että φ(x, y) on tosi kaikkien x:n ja y:n osalta. ∗13.12 koskee yhtäläisyyksien korvaamista yhtäläisyyksillä: jos x ja y ovat samoja, niin x:llä on ominaisuus ψ, jos ja vain jos myös y:llä on.
En ole nähnyt Principia Mathematican myöhempiä osia, koska kopioni loppuu jakson ∗56 jälkeen, ja aritmeettiset jutut ovat paljon myöhemmin. Mutta tässä lauseessa on selvästi 1+1=2:n merkitys, ja myöhempi lause (∗110.643), joka itse asiassa väittää 1+1=2:n, riippuu vahvasti tästä lauseesta.
Vaikka en olekaan täysin varma siitä, mitä myöhemmin tapahtuu (olen tuhlannut tähän jo aivan liikaa aikaa, jotta voisin käyttää vielä enemmän aikaa saadakseni koko version kirjastosta), voin tehdä valistuneen arvauksen. Principia Mathematica aikoo määritellä luvun 17 kaikkien 17-alkioisten joukkojen joukoksi ja samoin kaikkien muiden lukujen joukoksi; symbolin 2 käyttö kaikkien 2-alkioisten joukkojen joukon kuvaamiseen ennakoi tätä. Kaikkien tietyn kokoisten joukkojen joukot nimetään sitten ”kardinaaliluvuiksi”.
Principia Mathematica määrittelee kardinaalilukujen p ja q summan jotakuinkin näin: Otetaan p:stä edustava joukko a;a:lla on p elementtiä. Otetaan edustava joukko bjoukosta q; b:llä on q alkiota. Olkoon c =a∪b. Jos c on jonkin kardinaaliluvun r jäsen ja jos a ja b ovat erillisiä, niin p:n ja q:n summa on r.
Tämän määritelmän avulla voidaan todistaa tavanomaiset toivotut yhteenlaskun ominaisuudet, kuten x + 0 = x, x + y = y + x ja 1 + 1 = 2.
Erityisesti 1+1=2 seuraa suoraan lauseesta ∗54.43; se on juuri sitä, mitä haluamme, koska laskeaksemme 1+1, meidän on löydettävä kaksi toisistaan erillistä 1:n edustajaa ja otettava niiden yhteenliittymä; ∗54.43 väittää, että yhteenliittymän on oltava 2:n alkio, riippumatta siitä, minkä edustajan valitsemme, joten 1+1=2.
Post scriptum: Peter Norvig sanoo, että Principia Mathematican merkintätavan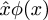 
circumflex on perimmäinen lähde sananlambda käytölle nimettömän funktion merkitsemiseen Lisp- ja Python-ohjelmointikielissä. Tiedät varmasti, että nämä kielet ovat saaneet sanan ”lambda” Alonzo Churchin käyttämästä kreikkalaisesta λ-kirjaimesta, jolla hän kuvasi funktioiden abstraktiota ”λ-laskennassaan”: Lispissä(lambda (u) B) on funktio, joka ottaa argumentin ja palauttaa B:n arvon; λ-laskennassa λu.B on funktio, joka ottaa argumentin ja palauttaa B:n arvon. Norvig sanoo, että Church aikoi alunperin kirjoittaa funktionλu.B muotoon û.B, mutta hänen tulostimensa ei osannut kirjoittaa circumflex-aksentteja. Niinpä hän harkitsi sirkumfleksin siirtämistä vasemmalle ja sen sijaan ison lambdan käyttämistä:Λu.B. Iso Λ näytti liikaa loogiselta ja ∧:lta, mikä oli hämmentävää, joten hän käytti sen sijaan pientä lambdaλ:tä.
Post post scriptum: Kaikki sanovat aina ”Russell ja Whitehead”.Google-tulokset ”Russell ja Whitehead” ovat kaksi kertaa suuremmat kuin ”Whitehead ja Russell”, esimerkiksi. Miksi? Kannessa ja nimiösivulla lukee ”Alfred North Whitehead and Bertrand Russell,F.R.S.”. Miten ja milloin Whitehead on menettänyt ykköspaikan?
permanent link