By Leave a Comment on Vapaan sivistystyön matematiikka

Verkot

Yksi viimeiseksi tavaksi esittää kiinteä kappale on käyttää verkkoa. Jos leikkaat verkon, voit taittaa sen hahmomalliksi. Verkkoja voidaan käyttää myös yksittäisen kiinteän kappaleen analysointiin. Tässä on esimerkki verkosta kuutiolle.

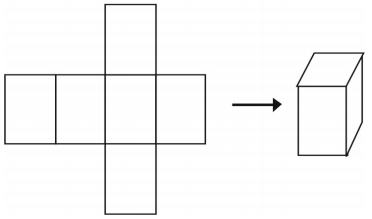
Verkon voi tehdä useammalla kuin yhdellä tavalla yhdelle kuviolle.

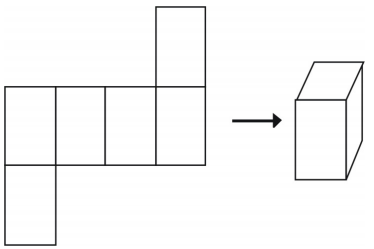
Mutta kaikki järjestelyt eivät luo kuutiota.

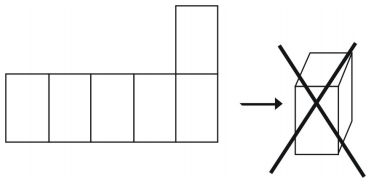
Esimerkki 1

Minkälaisen kuviolaskun verkko luo? Piirrä kuvio.

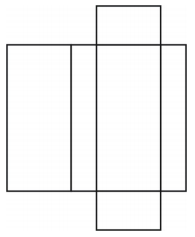
Verkko luo alla olevan kuvan mukaisen laatikon muotoisen suorakulmaisen prisman.

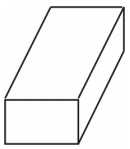
Esimerkki 2

Minkälaisen verkon pystyt piirtämään kuvaamasi kuvion esittämiseksi? Piirrä verkko.

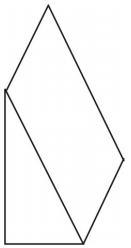
Kuvassa on esitetty prisman verkko. Muutkin verkot ovat mahdollisia.

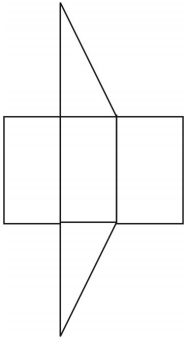
Kertausharjoitukset

Piirrä verkko jokaiselle seuraavista:

Vastaukset

Prismat

Prisma on kolmiulotteinen hahmo, jolla on pari samansuuntaista ja yhtenevää päätä eli perustaa. Prisman sivut ovat yhdensuuntaisia. Prismat tunnistetaan niiden pohjien perusteella.

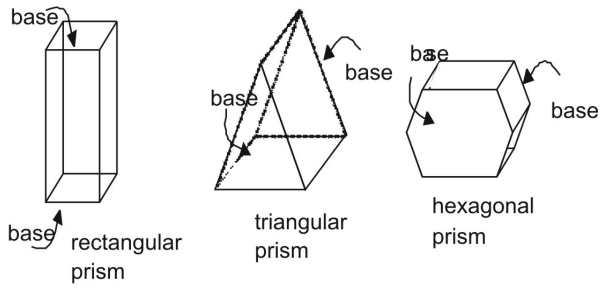
Prisman pinta-ala verkkojen avulla

Yllä olevat prismat ovat oikeita prismoja. Oikeassa prismassa sivusivut ovat kohtisuorassa prisman pohjia vastaan. Vertaa oikeaa prismaa vinoon prismaan, jossa sivut ja pohjat eivät ole kohtisuorassa.

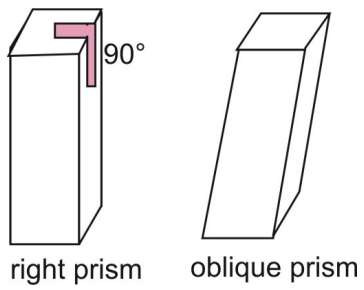
Kaksi pinta-alaan sovellettavaa postulaattia ovat pinta-alan kongruenssipostulaatti ja pinta-alan yhteenlaskupostulaatti.

Pinta-alan kongruenssipostulaatti: Jos kaksi monikulmiota (tai tasokuviota) ovat yhteneviä, niiden pinta-alat ovat yhteneviä.
Area Addition Postulate:

Voit käyttää verkkoa ja pinta-alojen yhteenlaskun postulaattia löytääksesi oikean prisman pinta-alan.

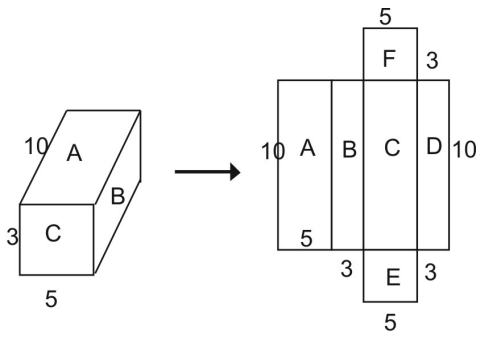
Verkosta näet, että koko prisman pinta-ala on yhtä suuri kuin verkon muodostavien lukujen summa:

Kokonaispinta-ala = pinta-ala A + pinta-ala B + pinta-ala C + pinta-ala C + pinta-ala D + pinta-ala E + pinta-ala F

Suorakulmion pinta-alan kaavan avulla näet, että suorakulmion A ala on:

A = l – w
A = 10 – 5 = 50 neliöyksikköä

Toisella tavalla muiden suorakulmioiden pinta-alat lisätään takaisin yllä olevaan yhtälöön.

Kokonaispinta-ala = pinta-ala A + pinta-ala B + pinta-ala C + pinta-ala D + pinta-ala E + pinta-ala F
Kokonaispinta-ala = (10 – 5) + (10 – 5) + (10 – 3) + (10 – 5) + (10 – 5) + (10 – 5) + (10 – 5) + (10 – 5). 3)
Kokonaispinta-ala = 50 + 30 + 50 + 30 + 15 + 15
Kokonaispinta-ala = 190 neliöyksikköä

Esimerkki 3

Etsitään prisman pinta-ala verkon avulla.

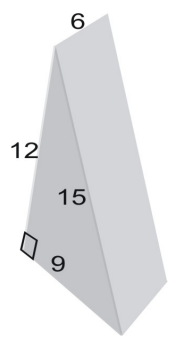
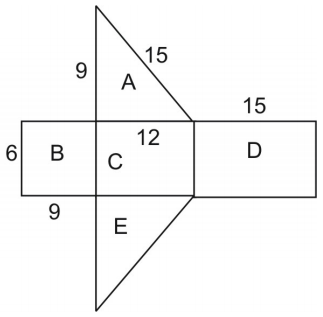
Verkon pinta-ala on yhtä suuri kuin kuvion pinta-ala. Kolmion pinta-alan löytämiseksi käytämme kaavaa:

\displaystyle{A}=\frac{1}{2}hb\\\ missä h on kolmion korkeus ja b on sen pohja.

Huomaa, että kolmiot A ja E ovat kongruentteja, joten voimme kertoa kolmion A pinta-alan luvulla 2.

\displaystyle\teksti{pinta-ala}=\teksti{pinta-ala }A+\teksti{pinta-ala }B+\teksti{pinta-ala }C+\teksti{pinta-ala }C+\teksti{pinta-ala }D+\teksti{pinta-ala }E\\\\
\displaystyle\teksti{pinta-ala}=2(\teksti{pinta-ala }A)+\teksti{pinta-ala³. }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\

Thus, pinta-ala on 324 neliöyksikköä.

Kertausharjoitukset

Kullekin seuraavista löydetään pinta-ala ovat a käyttäen verkkomenetelmää ja ympärysmitta

  3. Prisman pohja on suorakulmainen kolmio, jonka jalat ovat 3 ja 4 ja jonka näytä korkeus on 20. Mikä on prisman kokonaispinta-ala?
  4. Oikea kuusikulmainen prisma on 24 tuumaa korkea ja sen pohjat ovat säännöllisiä kuusikulmioita, joiden mitat ovat 8 tuumaa sivulta. Mikä on kokonaispinta-ala?
  5. Mikä on prisman tilavuus tehtävässä #4?

Seuraavissa kysymyksissä lato on viisikulmaisen prisman muotoinen, jonka mitat on ilmoitettu jaloissa:

  1. Minkä verran neliöjalkaa (kattoa lukuun ottamatta) on maalattavan ladon pinta-alaa?
  2. Jos gallona maalia peittää 250 neliöjalkaa, kuinka monta gallonaa maalia tarvitaan ladon maalaamiseen?
  3. Pahvilaatikko on täydellinen kuutio, jonka reuna on 17 tuumaa. Kuinka monta kuutiometriä siihen mahtuu?
  4. Uima-allas on 16 jalkaa leveä, 32 jalkaa pitkä ja tasaisesti 4 jalkaa syvä. Kuinka monta kuutiometriä vettä siihen mahtuu?
  5. Muropaketin pituus on 25 cm, leveys 9 cm ja korkeus 30 cm. Kuinka paljon muroja siihen mahtuu?

Vastaukset

Verkot ja ympärysmitta:

  1. 40.5 in2
  2. 838 cm2
  3. 252 neliöyksikköä
  4. 1484. Ongelman yksiköt on annettu tuumina, mutta kysymyksessä kysytään jalkoja.)
  5. 2048 kuutiojalkaa
  6. 6750 cm3

Lieriöt

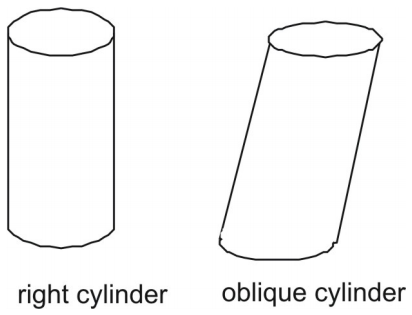
Lieriö on kolmiulotteinen hahmo, jolla on pari yhdensuuntaista ja yhtenevää ympyränmuotoista päätä eli pohjaa. Sylinterillä on yksi kaareva sivu, joka muodostaa tasoon asetettuna suorakulmion.

Kuten prismat, myös sylinterit voivat olla suorakulmaisia tai vinoja. Oikeaoppisen sylinterin sivu on kohtisuorassa sen pyöreitä pohjia vastaan. Vinon sylinterin sivu ei ole kohtisuorassa sen pohjia vastaan.

Sylinterin pinta-ala verkkojen avulla

Voit purkaa sylinterin verkoksi.

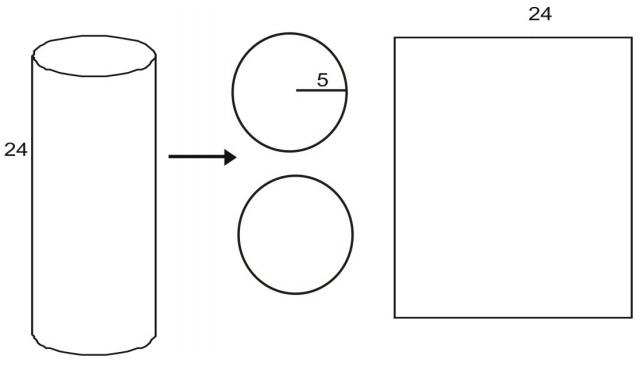
Kunkin pohjan pinta-ala saadaan ympyrän pinta-alasta:

A=\pi{r}^2\\\
A=\pi(5)^2\\\
A=25\pi\\
A\approx(25)(3.14)=78.5\\\\

Suorakulmaisen sivupinta-alan L pinta-ala saadaan leveyden ja korkeuden tulona. Korkeudeksi saadaan 24. Näet, että pinta-alan leveys on yhtä suuri kuin ympyränmuotoisen pohjan ympärysmitta.

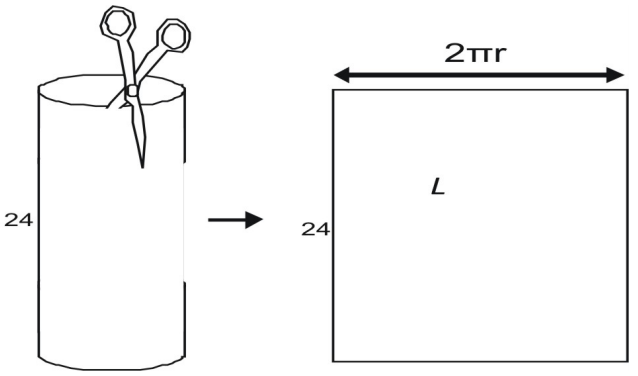
Leveyden löytämiseksi kuvitellaan, että purkkimaista sylinteriä otetaan saksilla erilleen. Kun leikkaat sivupinta-alaa, huomaat, että se on yhtä suuri kuin tölkin kannen ympärysmitta. Ympyrän kehä on C = 2πr, sivupinta-ala, L, on

L=2{\pi}rh\\\
L=2{\pi}(5)(24)\\\
L=240\pi\\\
L\approx(240)(3.14)=753.6\\\

Nyt voimme löytää koko sylinterin pinta-alan käyttämällä A = (kahden pohjan pinta-ala) + (sivusivun pinta-ala).

A=2(75.36)+753.6\\
A=904.32\\\

Voit nähdä, että kaavaa, jota käytimme kokonaispinta-alan löytämiseen, voidaan käyttää mille tahansa oikealle sylinterille.

Oikean sylinterin pinta-ala: Suorakulmaisen sylinterin, jonka säde on säde ja korkeus h, pinta-ala saadaan kaavalla A = 2B + L, jossa B on sylinterin kummankin pohjan pinta-ala ja L on sylinterin sivupinta-ala.

Esimerkki 4

Käytä verkkoa sylinterin pinta-alan selvittämiseksi.

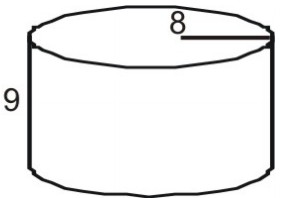
Piirrä ja merkitse ensin kuvion verkko.

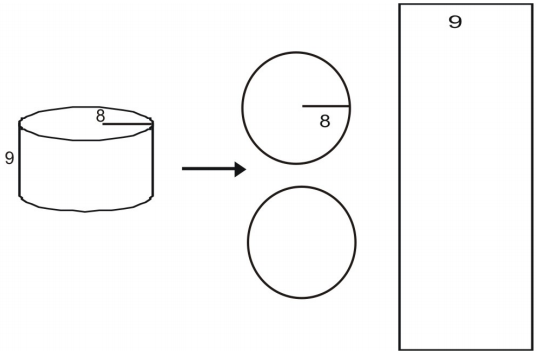
Lasketaan jokaisen pohjan pinta-ala.

A=\pi{r}^2\\\
A=\pi(8)^2\\\
A=64\pi\\
A\approx(64)(3.14)=200.96\\

Calculate L.

L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16\\

Löydä koko sylinterin pinta-ala.

A=2(200.96)+452.16\\
A=854.08\\\

Siten kokonaispinta-ala on noin 854,08 neliöyksikköä

Sylinterin pinta-ala kaavan avulla

Olet nähnyt, miten verkkojen avulla voidaan löytää sylinterin kokonaispinta-ala. Postulaatti voidaan purkaa niin, että saadaan yleinen kaava kaikille oikeille sylintereille.

A = 2B + L

Huomaa, että minkä tahansa sylinterin pohja, B, on: B = πr2

Minkä tahansa sylinterin sivupinta-ala, L, on:

L=\teksti{sivualueen leveys}\cdot\teksti{sylinterin korkeus}\\
L=\teksti{pohjan ympärysmitta}\cdot\teksti{sylinterin korkeus}\\
L=2\pi{r}\cdot{h}\\\\\

Yhdistämällä nämä kaksi yhtälöä yhteen saadaan:

Faktoroimalla yhtälöstä a saadaan:

Oikean sylinterin pinta-ala: Suorakulmainen sylinteri, jonka säde on r ja korkeus h, voidaan ilmaista seuraavasti:

A = 2πr2 + 2πrh

tai:

A = 2πr(r + h)

Voit käyttää kaavoja minkä tahansa suorakulmaisen sylinterin pinta-alan löytämiseen.

Esimerkki 5

Käytä kaavaa löytääksesi sylinterin pinta-ala.

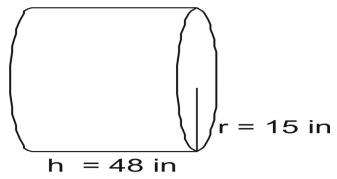
Kirjoita kaava ja korvaa arvot ja ratkaise.

A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\text{ neliötuumaa}\\\

Esimerkki 6

Löydä sylinterin pinta-ala.

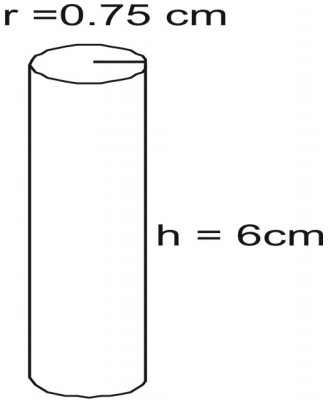
Kirjoita kaava ja korvaa arvot ja ratkaise.

A=2\pi{r}(r+h)\\
A=2(3.14)(0.75)\\
A=31.7925\text{ neliötuumaa}\\\

Esimerkki 7

Löydä sellaisen sylinterin korkeus, jonka säde on 4 cm ja pinta-ala 226,08 neliösenttimetriä.

Kirjoita kaava annettujen tietojen avulla ja ratkaise h.

A=2\pi{r}(r+h)\\\
226.08=2(3.14)(4)\\\
226.08=25.12\\\
226.08=100.48+25.12h\\\
5=h\\\

Pallot

Pallo on kolmiulotteinen hahmo, jolla on pallon muoto.

Palloja voidaan luonnehtia kolmella tavalla.

  • Pallo on kaikkien niiden pisteiden joukko, jotka sijaitsevat kiinteän etäisyyden r päässä yhdestä keskipisteestä O.
  • Pallo on pinta, joka syntyy, kun ympyrää käännetään minkä tahansa sen halkaisijan ympäri.

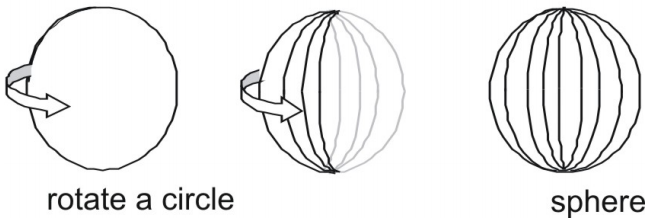
Pallon pinta-ala

Pallon pinta-alan kaavan voi päätellä tekemällä mittauksia palloista ja sylintereistä. Tässä näytetään pallo, jonka säde on 3, ja oikea sylinteri, jonka säde ja korkeus ovat molemmat 3, ja ilmaistaan pinta-ala π:nä.

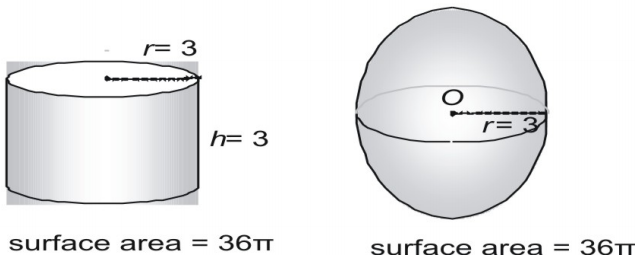
Kokeile nyt isompaa paria, jossa pinta-ala ilmaistaan desimaalimuodossa.

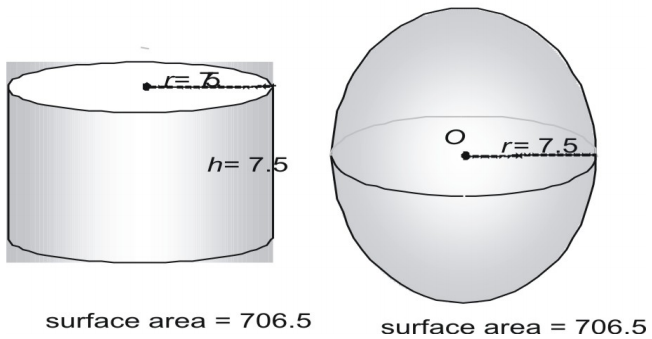
Kokeile kolmatta paria.

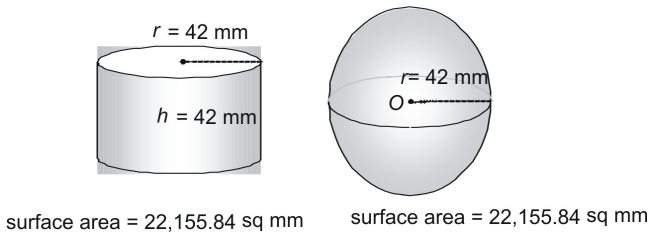
Onko sattumaa, että pallolla ja sylinterillä, jonka säde ja korkeus ovat yhtä suuret kuin pallon säde, on täsmälleen sama pinta-ala? Ei suinkaan! Itse asiassa antiikin kreikkalaiset käyttivät menetelmää, joka osoitti, että seuraavan kaavan avulla voidaan löytää minkä tahansa pallon (tai minkä tahansa sylinterin, jossa ) pinta-ala.

Pallon pinta-ala saadaan kaavalla: A = 4πr2

Esimerkki 8

Löydä sellaisen pallon pinta-ala, jonka säde on 14 jalkaa.

Käytä kaavaa.

A=4 \pi{r}^2 \\\\
A=4 \pi(14)^2 \\\
A=4 \pi(196)\ \\
A=784 \pi \\\
2461.76\text{ neliöjalkaa käyttäen }3.14\text{ varten \pi\\

Esimerkki 9

Löydä seuraavan kuvion pinta-ala π:n avulla.

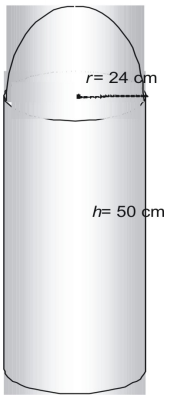
Hahmo muodostuu yhdestä puolikkaasta pallosta tai puolipallosta ja yhdestä sylinteristä ilman sen huippua.

A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half pallo})=2\pi(576)\\\
A(\text{puolikas pallo})=1152\pi\text{ neliö cm}\\

Löydä nyt sylinterin pinta-ala ilman sen huippua.

A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\

Thus, kokonaispinta-ala on 1152\pi+2976\pi=4128\pi\\

Kertausharjoitukset

  1. Löydä pallon säde, jonka tilavuus on 335 cm3.
  2. Määritä tämän muodon pinta-ala ja tilavuus:
  3. Pallon säde on 4. Selvitä sen tilavuus ja kokonaispinta-ala.
  4. Pallon säde on 5 cm3. Suorakulmaisella sylinterillä, jolla on sama säde, on sama tilavuus. Etsi sylinterin korkeus ja kokonaispinta-ala.
  5. Pallo: tilavuus = 296 cm3. Etsi halkaisija.
  6. Pallo: pinta-ala on 179 in2. Etsi säde.
  7. Tennispalloja, joiden halkaisija on 3,5 tuumaa, myydään kolmen kappaleen tölkeissä. Tölkki on sylinteri. Oletetaan, että pallot koskettavat purkkia sivuilta, ylhäältä ja alhaalta. Mikä on sen tilan tilavuus, jota tennispallot eivät vie?
  8. Pallon pinta-ala on 36π in2. Etsi sen tilavuus.
  9. Jättiläiskauha, jota nosturi käyttää, on puolipallon muotoinen, jonka säde on = 21 tuumaa. Kauha on täytetty sulatetulla kuumalla teräksellä. Kun teräs kaadetaan sylinterimäiseen varastosäiliöön, jonka säde on 28 tuumaa, sulanut teräs nousee kuinka monen tuuman korkeuteen?

Vastaukset

Huomaa, että näissä ongelmissa käytetään π:tä eikä 3,14:ää.

  1. 1. Säde = 4.31 cm
  2. Pinta-ala = 706.86 cm2
    Tilavuus = 1767.15 cm3
  3. Tilavuus = 268.08 yksikköä3
    Pinta-ala = 201.06 yksikköä2
  4. Korkeus = 20/3 yksikköä Kokonaispinta-ala = 366.52 yksikköä2
  5. Halkaisija = 8.27cm
  6. Säde = 3.77 tuumaa
  7. Sylinterin tilavuus = 32.16π in3 Tennispallojen tilavuus = 21.44π in3
    Tennispallojen viemä tila = 33.68 in3
  8. Tilavuus = 113.10 in3
  9. Sulan teräksen korkeus sylinterissä on 7.88 tuumaa

.

Vastaa

Sähköpostiosoitettasi ei julkaista.