Free Press

Dom, 18 Jun 2006

1+1=2

I Principia Mathematica di Whitehead e Russell sono famosi per aver impiegato mille pagine per dimostrare che 1+1=2. Naturalmente, dimostra anche molte altre cose. Se avessero voluto dimostrare solo che 1+1=2, probabilmente ci sarebbe voluta solo la metà dello spazio.

I Principia Mathematica è un libro strano, che vale la pena esaminare da un punto di vista storico e matematico. Fu scritto intorno al 1910, e la logica matematica era ancora agli inizi, fresca della trasformazione operata su di essa da Peano e Frege. La notazione è un po’ oscura, perché la notazione matematica si è evoluta sostanzialmente da allora. E molte delle tecniche semplici che ora diamo per scontate sono assenti. Come un programma per computer scritto male, gran parte della mole dei Principia Mathematica è costituita da codici ripetuti, sezioni separate che dicono essenzialmente le stesse cose, perché gli autori non hanno ancora imparato le tecniche che permetterebbero di combinare le sezioni in una sola.

Per esempio, la sezione ∗22, “Calcolo delle classi”, inizia definendo la relazione di sottoinsieme (∗22.01), e le operazioni di unione e intersezione di insiemi (∗22.02 e .03), il complemento di un insieme (∗22.04), e la differenza di due insiemi (∗22.05). Dimostra poi la commutatività e l’associatività dell’unione e dell’intersezione degli insiemi (∗22.51, .52, .57,e .7), varie proprietà come !!\alfa\cap\alpha = \alpha! (∗22.5) e simili, fino a teoremi come ∗22.92: !!\alfa\sottoinsieme\beta \freccia destra \alfa\cup(\beta -\alfa)!!.

La sezione ∗23 è “Calcolo delle relazioni” e inizia quasi esattamente allo stesso modo, definendo la relazione di sottorelazione (∗23.01), e le operazioni di unione e intersezione relazionale (∗23.02 e .03), il complemento di una relazione (∗23.04), e la differenza di due relazioni (∗23.05). In seguito dimostra la commutatività e associatività dell’unione e dell’intersezione relazionale (∗23.51, .52, .57,e .7), varie proprietà come !!\alpha\dotcap\alpha = \alpha! (∗22.5) e simili, fino a teoremi come ∗23.92: !!\alpha\dot\subset\beta \destra freccia \alpha\dot\cup(\beta \dot-alpha)!!.

La sezione ∗24 riguarda l’esistenza degli insiemi, l’insieme nullo !!\Lambda!!, l’insieme universale !!\rm V}!!le loro proprietà, e così via, e poi la sezione ∗24 è duplicata in ∗25 in una serie di teoremi sull’esistenza delle relazioni, la relazione nulla !!\dotLambda!!, la relazione universale !!\dot V}!!,le loro proprietà, e così via.

Così fecero Whitehead e Russell nel 1910. Come lo faremmo noi oggi? Una relazione tra S e T è definita come un sottoinsieme diS × T ed è quindi un insieme. L’unione, l’intersezione, la differenza e le altre operazioni sono esattamente le stesse per le relazioni e per gli insiemi, perché le relazioni sono insiemi. Tutti i teoremi sulle unioni e intersezioni di relazioni, come 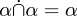, semplicemente spariscono, perché li abbiamo già dimostrati per gli insiemi e le relazioni sono insiemi. La relazione nulla è l’insieme nullo. La relazione universale è l’insieme universale.

Un’enorme quantità di altri macchinari sparisce nel 2006, a causa dell’unificazione di relazioni e insiemi. Principia Mathematica ha bisogno di una notazione speciale e di una definizione speciale per il risultato della restrizione di una relazione a quelle coppie il cui primo elemento è un membro di un particolare insieme S, o il cui secondo elemento è un membro di S, o entrambi i cui elementi sono membri di S; nel 2006 useremmo semplicemente l’ordinaria operazione di intersezione di insiemi e parleremmo di R ∩(S×B) o altro.

Whitehead e Russell non potevano farlo nel 1910 perché mancava un macchinario cruciale: la coppia ordinata. Nel 1910 nessuno sapeva come costruire una coppia ordinata solo con la logica e gli insiemi. Nel 2006 (o anche nel 1956), definiremmo la coppia ordinata <a, b> come l’insieme {{a}, {a, b}}. Poi dimostreremmo come ateorema che <a, b> = <c, d> se e solo se a=c e b=d, usando le proprietà degli insiemi. Allora definiremmo A×B come l’insieme di tutti i p tali che p = <a,b> ∧ a ∈ A ∧ b∈ B. Poi definiremmo una relazione sugli insiemi A e B come un sottoinsieme di A×B. Allora otterremmo gratuitamente tutto ∗23 e ∗25 e molto di ∗33 e ∗35 e ∗36, e probabilmente anche molta altra roba.

(A proposito, la cosa {{a}, {a, b}} è stata inventata da Kuratowski. Di solito viene attribuita a Norbert Wiener, ma l’idea di Wiener, sebbene simile, era in realtà più complicata.)

Non ci sono coppie ordinate nei Principia Mathematica, se non implicitamente. Ci sono a malapena degli insiemi. Whitehead e Russell vogliono basare tutto sulla logica. Per Whitehead e Russell, la nozione fondamentale è la “funzione proposizionale”, che è una funzione φ la cui uscita è un valore di verità. Per ogni funzione di questo tipo, c’è un insieme corrispondente, che essi denotano con !!\hat x\phi(x)!!, l’insieme di tutti gli x tali che φ(x) è vero. Per Whitehead e Russell, l’arelazione è implicata da una funzione proposizionale di due variabili, analogamente al modo in cui un insieme è implicato da una funzione proposizionale di una variabile. Nel 2006, rinunciamo alle “funzioni di due variabili” e parliamo solo di funzioni il cui (unico) argomento è una coppia ordinata; una relazione diventa allora l’insieme di tutte le coppie ordinate per le quali una funzione è vera.

Russell avrebbe detto che la scoperta del tratto di Sheffers (un singolo operatore logico dal quale si possono costruire tutti gli altri operatori logici) era un enorme progresso e avrebbe cambiato tutto. Questo ci sembra strano ora, perché la scoperta del tratto di Sheffer sembra così semplice, e in realtà non cambia nulla di importante. Basta aggiungere una nota all’inizio del capitolo 1 che dica che ∼p e p∨q sonoabbreviazioni per p|p ep|p.|.q|q, rispettivamente, dimostrare i cinque assiomi fondamentali, e lasciare tutto il resto uguale. Ma Russell potrebbe con un po’ di giustizia dire la stessa cosa della scoperta che le coppie ordinate possono essere interpretate come insiemi, una semplice scoperta che avrebbe davvero trasformato i Principia Mathematica in un’opera completamente diversa. Questo avviene abbastanza tardi nei Principia Mathematica, nella sezione ∗102. La mia versione integrale arriva solo a ∗56, ma è abbastanza lontano per arrivare all’importante teorema precursore, ∗54.43, scannerizzato qui sotto:

La notazione può essere schiacciante, quindi concentriamoci solo sull’enunciato del teorema, ignorando tutto il resto, anche l’utile nota in fondo:

Questo è il teorema che viene dimostrato; ciò che segue è la prova.

Ora dovrei spiegare la notazione, che è cambiata un po’ dal 1910. Prima di tutto, Principia Mathematica usa la notazione “punti” di Peano per disambiguare la precedenza, mentre ora usiamo le parentesi. La notazione a punti richiede un po’ di tempo per abituarsi, ma ha alcuni distinti vantaggi rispetto alle parentesi. L’idea è solo che si indica il raggruppamento mettendo dei punti, così che (1+2)×(3+4)&times(5+6) si scrive come1+2.×.3+4.×.5+6. La sotto-formula centrale è tra una coppia di punti. Anche la sottoformula (1+2) è tra una coppia di punti, ma il punto all’estremità sinistra è superfluo, e lo omettiamo; allo stesso modo, la sottoformula (5+6) è delimitata da un punto a sinistra e dalla fine della formula a destra.

E se avete bisogno di annidare le parentesi? Allora si usano più punti. Un doppio punto (:) è come un punto singolo, ma più forte. Per esempio, scriviamo ((1+2)×3)+4 come 1+2 . × 3 : + 4, e il doppio punto isola l’intera espressione 1+2 . × 3 in una sotto-formula singola a cui si applica il +4.

A volte si ha bisogno di più livelli di precedenza, e allora si usano punti tripli (.: e :.) e quadrupli (::). Questa formula, come vedete, ha doppi e tripli punti. Traducendo i puntini nella notazione standard della parentesi, abbiamo $$ast54.43. \vdash ((\alpha, \beta \in 1) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \in 2)))$$. Questo ha un aspetto più disordinato rispetto alla versione con i punti, e con formule incomplicate si possono avere problemi a capire quali parentesi corrispondono con quali. Con i punti, è sempre facile. Quindi penso che sia un po’ spiacevole che questa convenzione sia caduta in disuso.

Il simbolo !!\vdash!! non è cambiato; significa che la formula a cui si applica è asserita essere vera. !!\supset!! è un’implicazione logica, e !\equiv!! è un’equivalenza logica. Λ è l’insieme vuoto, che oggi si scrive ∅. ∩ ∪ e ∈ hanno il loro significato moderno: ∩ e ∪ sono gli operatori di intersezione e unione degli insiemi, e x∈y significa che x è un elemento dell’insieme y.

I restanti punti sono semantici. 1dimostra l’insieme di tutti gli insiemi che hanno esattamente un elemento. Cioè, è l’insieme { c : esiste a tale che c = {a } }. I teoremi su 1 includono, per esempio:

• che Λ∉1 (∗52.21),
• che se α∈1 allora esiste qualche x tale che α ={x} (∗52.1), e
• che {x}∈1 (∗52.22).

2 è similmente l’insieme di tutti gli insiemi che hanno esattamente due elementi. Un importante teorema su 2 è ∗54.3, che dice $$ ∗54.3. \vdash 2 = \hat\alpha\ (\esiste x) \> .\>xin\alpha \> . \Ecco di nuovo il teorema ∗54.43:

Afferma che se gli insiemi α e β hanno ciascuno esattamente un elemento, allora sono disgiunti (cioè non hanno elementi in comune) se e solo se la loro unione ha esattamente due elementi.

La dimostrazione, che appare nella scansione qui sopra dopo la parola “Dem.” (abbreviazione di “dimostrazione”) va così:

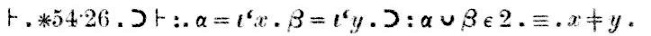
“Il teorema ∗54.26implica che se α = {x} e β = {y}, alloraα∪β ha 2 elementi se e solo se x è diverso da y.”

“Per il teorema ∗51.231, quest’ultimo bit (x è diverso day) è vero se e solo se {x} e {y} sono disgiunti.”

“Per ∗13.12, quest’ultimo bit ({x} e {y} sono disgiunti) è vero se e solo se α e β stessi sono disgiunti”. La conclusione parziale a questo punto, che è etichettata (1), è che se α = {x} e β ={y}, allora α∪β ∈ 2 se e solo seα∩β = Λ.

La dimostrazione continua: “La conclusione (1), con i teoremi ∗11.11 e ∗11.35, implica che se esistono x e y in modo che α sia{x} e β sia {y}, allora α∪β ∈ 2 se e solo se α e β sono disgiunti.” Questa conclusione è etichettata (2).

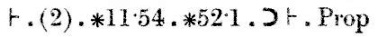
Infine, la conclusione (2), insieme ai teoremi ∗11.54 e ∗52.1, implica il teorema che volevamo dimostrare.

Forse la cosa da notare qui è come i passi siano molto piccoli.∗54.26, da cui questo teorema dipende pesantemente, è quasi lo stesso; esso afferma che {x}∪{y} ∈ 2 se e solo se x≠y. ∗54.26, a sua volta, dipende da ∗54.101, che dice che α ha 2 elementi se e solo se esistono x ey, non uguali, tali che α = {x} ∪{y}. ∗54.101 è solo un po’ diverso dalla definizione di 2. Il teorema ∗51.231 dice che {x} e {y} sono disgiunti se e solo se x e y sono diversi.∗52.1 è una proprietà fondamentale di 1; l’abbiamo visto prima.

Gli altri teoremi citati nella dimostrazione sono questioni tecniche molto piccole. ∗11.54 dice che si può prendere un’asserzione che due cose esistono e separarla in due asserzioni, ciascuna delle quali afferma che una delle cose esiste. ∗11.11 è ancora più sottile: dice che se φ(x, y) è sempre vero, allora si può attaccare un quantificatore universale e asserire che φ(x, y) è vero per tutti gli x e gli y. ∗13.12 riguarda la sostituzione di uguali per uguali: se x e y sono uguali, allora x possiede una proprietà ψ se e solo se anche y lo fa.

Non ho visto le parti successive dei Principia Mathematica, perché la mia copia si ferma dopo la sezione ∗56, e la roba aritmetica è molto più tardi. Ma questo teorema ha chiaramente il senso di 1+1=2, e il teorema successivo (∗110.643) che effettivamente afferma 1+1=2 dipende fortemente da questo.

Anche se non sono completamente sicuro di quello che succederà in seguito (ho già perso troppo tempo su questo per metterci più tempo per ottenere la versione completa dalla biblioteca) posso fare un’ipotesi educata. Principia Mathematica definirà il numero 17 come l’insieme di tutti gli insiemi di 17 elementi e, analogamente, ogni altro numero; l’uso del simbolo 2 per rappresentare l’insieme di tutti gli insiemi di 2 elementi prefigura questo. Gli insiemi di tutti gli insiemi di una certa grandezza saranno allora identificati come “numeri cardinali”.

I Principia Mathematica definiranno la somma dei numeri cardinali p e q in questo modo: prendi un insieme rappresentativo a da p; a ha p elementi. Prendiamo un insieme rappresentativo b da q; b ha q elementi. Sia c =a∪b. Se c è un membro di qualche numero cardinale r, e se a e b sono disgiunti, allora la somma di p e q è r.

Con questa definizione, puoi dimostrare le solite proprietà desiderabili dell’addizione, come x + 0 = x, x + y = y + x, e 1 + 1 = 2.

In particolare, 1+1=2 segue direttamente dal teorema ∗54.43; è proprio quello che vogliamo, perché per calcolare 1+1, dobbiamo trovare due rappresentanti disgiunti di 1, e prendere la loro unione; ∗54.43 afferma che l’unione deve essere un elemento di 2, indipendentemente da quali rappresentanti scegliamo, così che 1+1=2.

Post scriptum: Peter Norvig dice che il circonflesso nella notazione dei Principia Mathematica 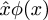è la fonte ultima dell’uso della parolaambda per indicare una funzione anonima nei linguaggi di programmazione Lisp e Python. Sono sicuro che sapete che questi linguaggi prendono “lambda” dall’uso della lettera greca λ da Alonzo Church per rappresentare l’astrazione delle funzioni nel suo “λ-calculus”: In Lisp,(lambda (u) B) è una funzione che prende un argomento e restituisce il valore di B; nel λ-calculus, λu.B è una funzione che prende un argomento e restituisce il valore di B. Norvig dice che Church aveva originariamente intenzione di scrivere la funzioneλu.B come û.B, ma la sua stampante non poteva fare gli accenti circonflessi. Così considerò di spostare il circonflesso a sinistra e di usare invece una lambda maiuscola:Λu.B. Il Λ maiuscolo sembrava troppo simile a ∧ e ∧, il che confondeva, così usò invece lambdaλ minuscolo.

Post post scriptum: Tutti dicono sempre “Russell e Whitehead”.I risultati di Google per “Russell e Whitehead” superano di due a uno quelli per “Whitehead e Russell”, per esempio. Perché? La copertina e il frontespizio dicono “Alfred North Whitehead e Bertrand Russell, F.R.S.”. Come e quando Whitehead ha perso la prima posizione?

link permanente