- Obiettivi di apprendimento
- Reti
- Esempio 1
- Esempio 2
- Esercizi di revisione
- Risposte
- Prismi
- Superficie di un prisma usando le reti
- Esempio 3
- Esercizi di ripasso
- Risposte
- Cilindri
- Superficie di un cilindro usando le reti
- Esempio 4
- Superficie di un cilindro usando una formula
- Esempio 5
- Esempio 6
- Esempio 7
- Sfere
- Superficie di una sfera
- Esempio 8
- Review Exercises
- Risposte
Obiettivi di apprendimento
- Comprendere le reti.
- Utilizzare le reti per rappresentare i prismi.
- Trova la superficie di un prisma.
- Trova la superficie dei cilindri.
- Trova la superficie di una sfera.
Reti
Un ultimo modo per rappresentare un solido è usare una rete. Se ritagliate una rete potete piegarla in un modello di una figura. Le reti possono anche essere usate per analizzare un singolo solido. Ecco un esempio di rete per un cubo.
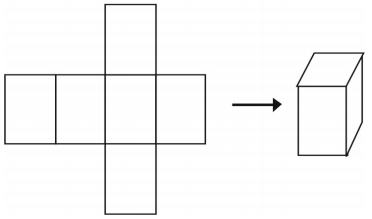
C’è più di un modo per fare una rete per una singola figura.
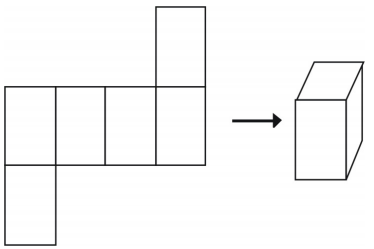
Tuttavia, non tutte le disposizioni creeranno un cubo.
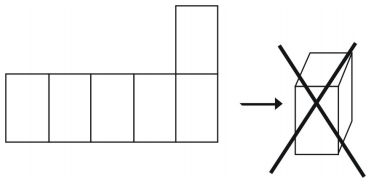
Esempio 1
Che tipo di figura crea la rete? Disegna la figura.
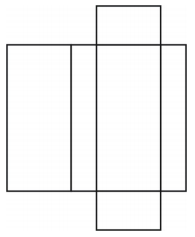
La rete crea un prisma rettangolare a forma di scatola come mostrato sotto.
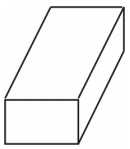
Esempio 2
Che tipo di rete puoi disegnare per rappresentare la figura mostrata? Disegna la rete.
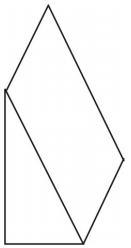
È mostrata una rete per il prisma. Altre reti sono possibili.
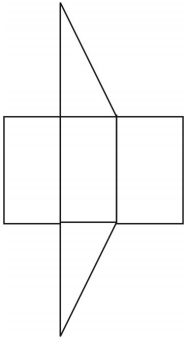
Esercizi di revisione
Disegna una rete per ciascuno dei seguenti elementi:
Risposte
Prismi
Un prisma è una figura tridimensionale con una coppia di estremità o basi parallele e congruenti. I lati di un prisma sono parallelogrammi. I prismi sono identificati dalle loro basi.
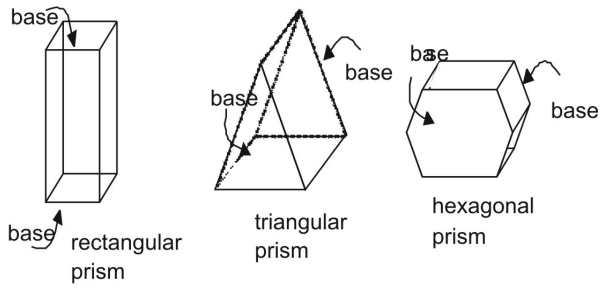
Superficie di un prisma usando le reti
I prismi sopra sono prismi retti. In un prisma retto, i lati laterali sono perpendicolari alle basi del prisma. Confronta un prisma retto con un prisma obliquo, in cui i lati e le basi non sono perpendicolari.
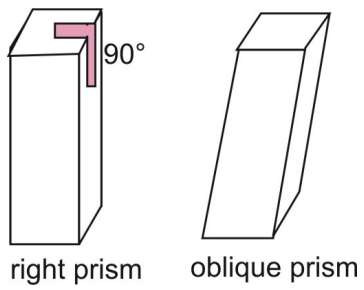
Due postulati che si applicano all’area sono il postulato di congruenza dell’area e il postulato di addizione dell’area.
Puoi usare una rete e il postulato dell’addizione delle aree per trovare la superficie di un prisma retto.
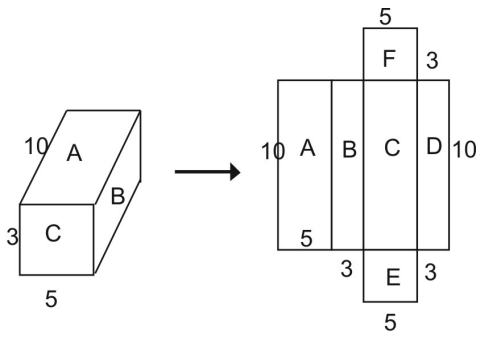
Dalla rete, si può vedere che la superficie dell’intero prisma è uguale alla somma delle cifre che compongono la rete:
Superficie totale = area A + area B + area C + area D + area E + area F
Utilizzando la formula dell’area di un rettangolo, si può vedere che l’area del rettangolo A è:
A = l – w
A = 10 – 5 = 50 unità quadrate
Similmente, le aree degli altri rettangoli vengono reinserite nell’equazione precedente.
Superficie totale = area A + area B + area C + area D + area E + area F
Superficie totale = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3)
Superficie totale = 50 + 30 + 50 + 30 + 15 + 15
Superficie totale = 190 unità quadrate
Esempio 3
Utilizzare una rete per trovare la superficie del prisma.
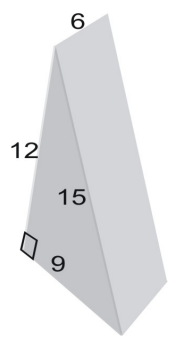
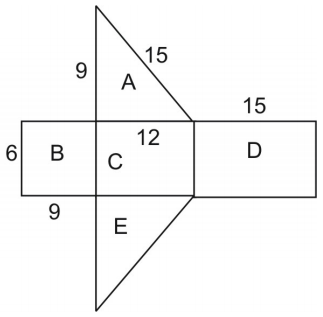
L’area della rete è uguale alla superficie della figura. Per trovare l’area del triangolo, usiamo la formula:
displaystyle{A}=frac{1}{2}hb\ dove h è l’altezza del triangolo e b è la sua base.
Nota che i triangoli A ed E sono congruenti quindi possiamo moltiplicare l’area del triangolo A per 2.
displaystyle{text{area}=A+text{area }B+text{area }C+text{area }D+text{area }E
displaystyle{text{text{=2(\text{area }A)+\text{area} }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\
Thus, la superficie è di 324 unità quadrate.
Esercizi di ripasso
Per ognuno dei seguenti trovare la superficie sono a usando il metodo delle reti e il perimetro


- La base di un prisma è un triangolo rettangolo le cui gambe sono 3 e 4 e l’altezza è 20. Qual è l’area totale del prisma?
- Un prisma esagonale destro è alto 24 pollici e ha basi che sono esagoni regolari che misurano 8 pollici di lato. Qual è la superficie totale?
- Qual è il volume del prisma nel problema #4?
Nelle seguenti domande, un fienile ha la forma di un prisma pentagonale con dimensioni indicate in piedi:

- Quanti piedi quadrati (escluso il tetto) ci sono sulla superficie del fienile da dipingere?
- Se un gallone di vernice copre 250 piedi quadrati, quanti galloni di vernice sono necessari per dipingere il fienile?
- Una scatola di cartone è un cubo perfetto con un bordo di 17 pollici. Quanti piedi cubi può contenere?
- Una piscina è larga 16 piedi, lunga 32 piedi ed è uniformemente profonda 4 piedi. Quanti piedi cubi d’acqua può contenere?
- Una scatola di cereali ha lunghezza 25 cm, larghezza 9 cm e altezza 30 cm. Quanti cereali può contenere?
Risposte
Reti e perimetro:
- 40,5 in2
- 838 cm2
- 252 unità quadrate
- 1484.6 unità quadrate
- 3990,7 pollici cubi
Il fienile:
- 2450 piedi quadrati
- 10 galloni di vernice
- 2,85 piedi cubi (attenzione qui. Le unità nel problema sono date in pollici ma la domanda chiede piedi.)
- 2048 piedi cubici
- 6750 cm3
Cilindri
Un cilindro è una figura tridimensionale con una coppia di estremità circolari parallele e congruenti, o basi. Un cilindro ha un solo lato curvo che forma un rettangolo quando è disposto in piano.
Come i prismi, i cilindri possono essere retti o obliqui. Il lato di un cilindro retto è perpendicolare alle sue basi circolari. Il lato di un cilindro obliquo non è perpendicolare alle sue basi.
Superficie di un cilindro usando le reti
Si può decostruire un cilindro in una rete.
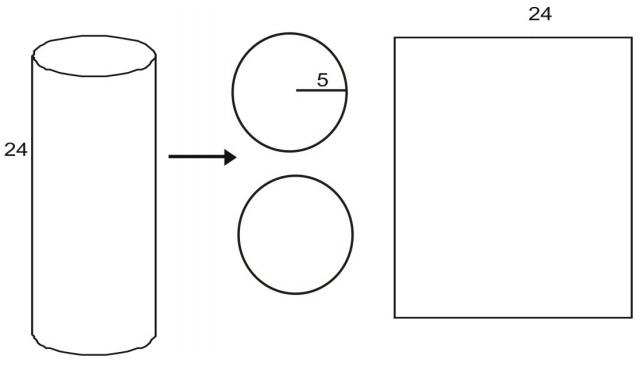
L’area di ogni base è data dall’area di un cerchio:
A=\pi{r}^2\\
A=\pi(5)^2\
A=25\pi\
Approx(25)(3.14)=78.5\
L’area dell’area laterale rettangolare L è data dal prodotto di una larghezza e un’altezza. L’altezza è data come 24. Puoi vedere che la larghezza dell’area è uguale alla circonferenza della base circolare.
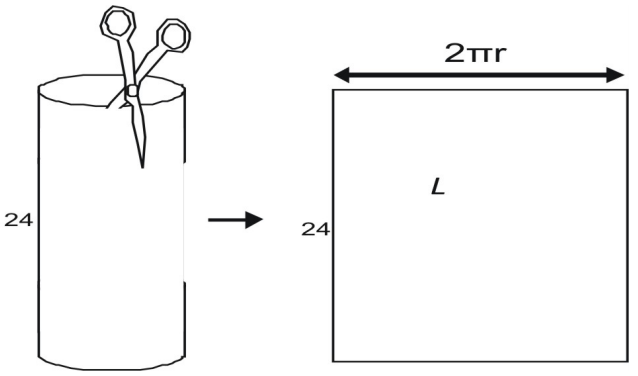
Per trovare la larghezza, immagina di tagliare con le forbici un cilindro simile a una lattina. Quando si taglia l’area laterale, si vede che è uguale alla circonferenza della cima della lattina. La circonferenza di un cerchio è data da C = 2πr, l’area laterale, L, è
L=2{\pi}rh\
L=2{\pi}(5)(24)\
L=2{\pi}(5)(24)\L=240\pi\
L=(240)(3.14)=753.6\\
Ora possiamo trovare l’area dell’intero cilindro usando A = (area delle due basi) + (area del lato laterale).
A=2(75.36)+753.6\\\
A=904.32\
Si può vedere che la formula che abbiamo usato per trovare l’area totale della superficie può essere usata per qualsiasi cilindro retto.
Esempio 4
Usa una rete per trovare l’area della superficie del cilindro.
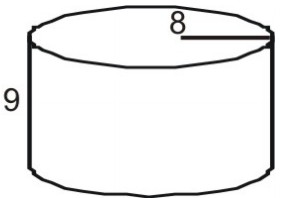
Prima disegna ed etichetta una rete per la figura.
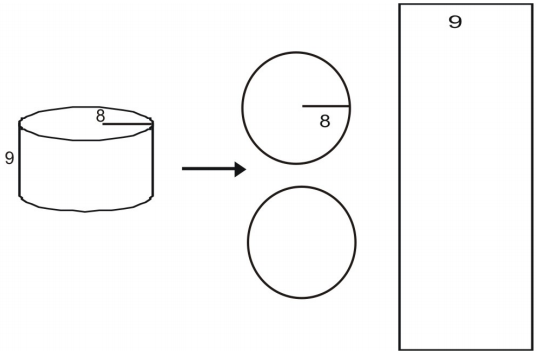
Calcolare l’area di ogni base.
A=\pi{r}^2\\
A=\pi(8)^2\\
A=64\pi\
A circa(64)(3.14)=200.96\\
Calculate L.
L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16\
Trova l’area dell’intero cilindro.
A=2(200.96)+452.16\
A=854.08\
Quindi, la superficie totale è approssimativamente 854,08 unità quadrate
Superficie di un cilindro usando una formula
Hai visto come usare le reti per trovare la superficie totale di un cilindro. Il postulato può essere scomposto per creare una formula generale per tutti i cilindri retti.
A = 2B + L

Nota che la base, B, di qualsiasi cilindro è: B = πr2
L’area laterale, L, per qualsiasi cilindro è:
L = larghezza dell’area laterale
Mettendo insieme le due equazioni si ottiene:
Fattorizzando a dall’equazione si ottiene:
L’area della superficie di un cilindro retto: Un cilindro retto con raggio r e altezza h può essere espresso come:
A = 2πr2 + 2πrh
oppure:
A = 2πr(r + h)
Puoi usare queste formule per trovare l’area di qualsiasi cilindro retto.
Esempio 5
Usa la formula per trovare la superficie del cilindro.
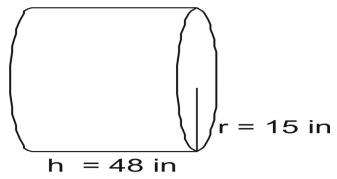
Scrivi la formula e sostituisci i valori e risolvi.
A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\testo{ pollici quadrati}{767676>
Esempio 6
Trova l’area della superficie del cilindro.
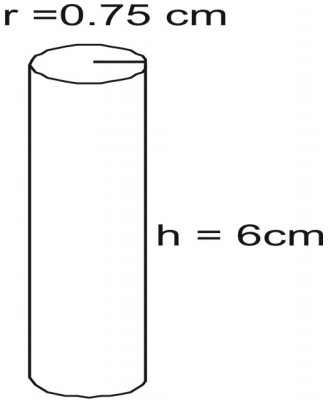
Scrivere la formula e sostituire i valori e risolvere.
A=2\pi{r}(r+h)\\
A=2(3,14)(0,75)\
A=31.7925\testo{ pollici quadrati}{
Esempio 7
Trovare l’altezza di un cilindro che ha raggio 4cm e superficie di 226,08 cm quadrati.
Scrivere la formula con le informazioni date e risolvere per h.
A=2\pi{r}(r+h)\
226.08=2(3.14)(4)\
226.08=25.12\
226.08=100.48+25.12h\
5=h\\7676>
Sfere
Una sfera è una figura tridimensionale che ha la forma di una palla.

Le sfere possono essere caratterizzate in tre modi.
- Una sfera è l’insieme di tutti i punti che giacciono ad una distanza fissa r da un singolo punto centrale O.
- Una sfera è la superficie che risulta quando un cerchio viene ruotato su uno qualsiasi dei suoi diametri.
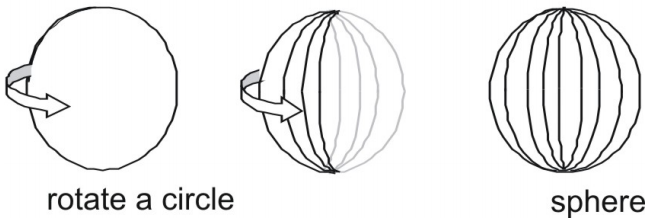
Superficie di una sfera
Puoi dedurre la formula per la superficie di una sfera prendendo misure di sfere e cilindri. Qui mostriamo una sfera con un raggio di 3 e un cilindro destro con raggio e altezza di 3 ed esprimiamo l’area in termini di π.
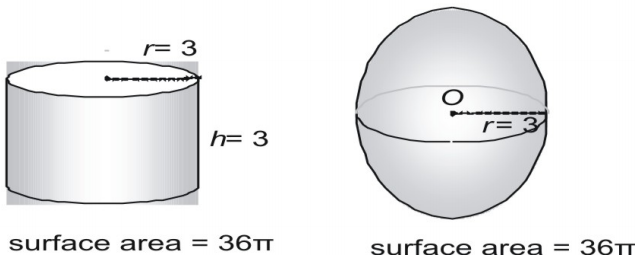
Prova ora con una coppia più grande, esprimendo l’area della superficie in forma decimale.
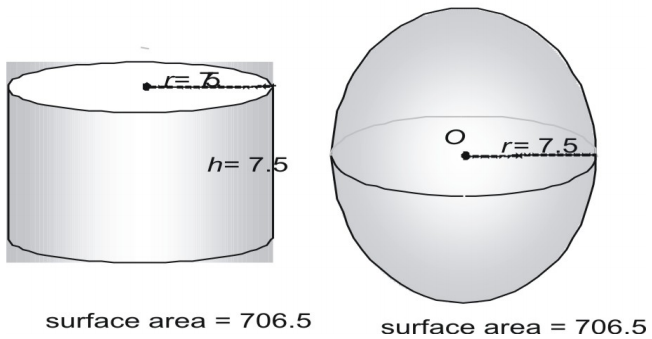
Guarda una terza coppia.
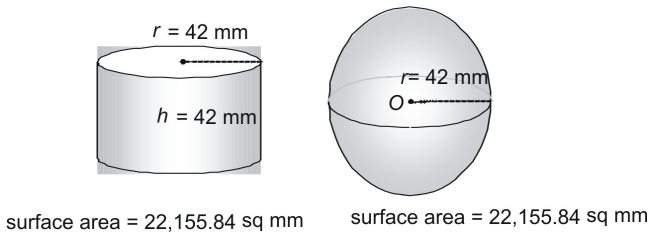
È una coincidenza che una sfera e un cilindro il cui raggio e la cui altezza sono uguali al raggio della sfera abbiano esattamente la stessa superficie? Assolutamente no! Infatti, gli antichi greci usavano un metodo che dimostrava che la seguente formula può essere usata per trovare l’area della superficie di qualsiasi sfera (o qualsiasi cilindro in cui ).
Esempio 8
Trova l’area della superficie di una sfera con un raggio di 14 piedi.
Usa la formula.
A=4\pi{r}^2\\
A=4\pi(14)^2\
A=4\pi(196)\
A=784\pi\
2461.76\code(0144)}piedi quadrati usando }3.14\code(0144)}per }pi\code(0144)^3.14\code(0144)^ per }pi\code(0144)^3>Esempio 9
Trova l’area della seguente figura in termini di π.
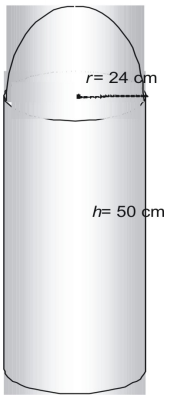
La figura è fatta di una mezza sfera o emisfero, e un cilindro senza la sua sommità.
A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half sfera})=2\pi(576)\
A(\testo{metà sfera})=1152\pi{ cm²}
Ora trovate l’area del cilindro senza la sua sommità.
A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\
Thus, la superficie totale è 1152\pi+2976\pi=4128\pi\
Review Exercises
- Trova il raggio della sfera che ha un volume di 335 cm3.
- Determina la superficie e il volume di questa forma:

- Il raggio di una sfera è 4. Trova il suo volume e la superficie totale.
- Una sfera ha un raggio di 5. Un cilindro retto, avente lo stesso raggio, ha lo stesso volume. Trova l’altezza e la superficie totale del cilindro.
- Sfera: volume = 296 cm3. Trova il diametro.
- Sfera: la superficie è 179 in2. Trovare il Raggio.
- Palloni da tennis con un diametro di 3,5 pollici sono venduti in barattoli da tre. La lattina è un cilindro. Supponiamo che le palle tocchino la lattina sui lati, in alto e in basso. Qual è il volume dello spazio non occupato dalle palle da tennis?
- Una sfera ha una superficie di 36π in2. Trova il suo volume.
- Una paletta gigante, azionata da una gru, ha la forma di una semisfera di raggio = 21 pollici. La paletta è piena di acciaio caldo fuso. Quando l’acciaio viene versato in un serbatoio cilindrico che ha un raggio di 28 pollici, l’acciaio fuso salirà ad un’altezza di quanti pollici?
Risposte
Nota che questi problemi usano π non 3,14.
- 1. Raggio = 4,31 cm
- Superficie = 706,86 cm2
Volume = 1767,15 cm3 - Volume = 268,08 unità3
Superficie = 201,06 unità2 - Altezza = 20/3 unità superficie totale = 366,52 unità2
- Diametro = 8,27cm
- Raggio = 3.77 pollici
- Volume del cilindro = 32.16π in3 volume delle palle da tennis = 21.44π in3
Volume dello spazio non occupato dalle palle da tennis = 33.68 in3 - Volume = 113.10 in3
- Altezza dell’acciaio fuso nel cilindro sarà 7.88 pollici



