Amortowana analiza jest używana dla algorytmów, które mają drogie operacje, które zdarzają się rzadko.

Amortowana analiza złożoności jest najczęściej używana ze strukturami danych, które mają stan, który utrzymuje się między operacjami.Podstawową ideą jest to, że kosztowna operacja może zmienić stan tak, że najgorszy przypadek nie może wystąpić ponownie przez długi czas, amortyzując w ten sposób swój koszt.
Pozwól T1, T2, …, Tk być złożonością sekwencji operacji na strukturze danych. Amortyzowana złożoność pojedynczej operacji w tej sekwencji to(T1 + T2 + …+ Tk) / k.
Przykład: tablica dynamiczna
W tablicy dynamicznej elementy są przechowywane na początku bazowej tablicy stałej, a pozostałe pozycje są nieużywane.
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Tutaj widok pamięci podczas dołączania elementów 2, 7, 1, 3, 8, 4 do początkowo pustej tablicy o pojemności 2.
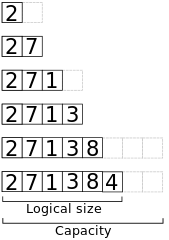
Czas najgorszego przypadku
Najgorsza złożoność czasowa operacji dołączania elementu do tablicy o długości n, przy użyciu tego algorytmu, wynosi Θ(n).Jeśli tablica jest pełna, algorytm przydziela nową tablicę o długości 2n, a następnie kopiuje elementy ze starej tablicy do nowej.
Pewnie ten wynik jest zbyt pesymistyczny.Kolejne n operacji dołączania będzie znacznie tańsze – każda z nich będzie przebiegać w stałym czasie, ponieważ nowo zaalokowana tablica ma miejsce na wszystkie nowe elementy.
Czas zamortyzowany
Analiza czasu zamortyzowanego daje znacznie lepsze zrozumienie algorytmu.
Rozważmy sekwencję n operacji dołączania, w której zaczynamy od tablicy o długości 1. Dokładna analiza pokazuje, że całkowity czas tych operacji to tylko Θ(n).
- W sumie będzie n operacji przypisania i przyrostu w czasie stałym.
- Zmiana rozmiaru nastąpi tylko przy operacjach 1, 2, 4, …, 2k, w sumie 1 + 2 + 4 + …+ 2k = 2-2k – 1 operacji kopiowania elementów w czasie stałym. Ponieważ 2k ≤ n, jest to co najwyżej 2n – 1.
Stąd, zamortyzowana złożoność czasowa dla pojedynczej operacji append wynosi Θ(1).
Więcej o analizie algorytmów

Złożoność czasowa: Policz swoje kroki

Notacja Big O
.