By Leave a Comment on Mathematics for the Liberal Arts

Siatki

Jednym z ostatnich sposobów reprezentowania bryły jest użycie siatki. Jeśli wyciąć siatkę można złożyć go do modelu figury. Siatki mogą być również użyte do analizy pojedynczej bryły. Oto przykład siatki dla sześcianu.

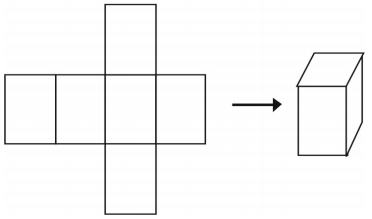
Jest więcej niż jeden sposób na wykonanie siatki dla pojedynczej figury.

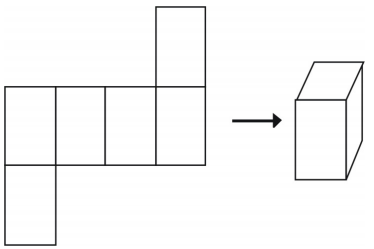
Jednakże nie wszystkie układy utworzą sześcian.

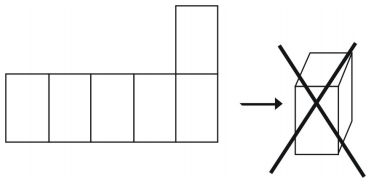
Przykład 1

Jaką figurę tworzy siatka? Narysuj tę figurę.

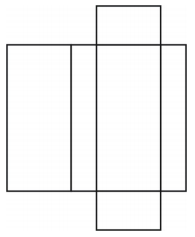
Sieć tworzy graniastosłup prostokątny w kształcie pudełka, jak pokazano poniżej.

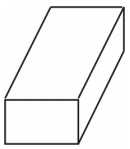
Przykład 2

Jaką siatkę możesz narysować, aby przedstawić przedstawioną figurę? Narysuj taką siatkę.

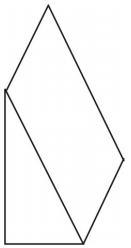
Przedstawiono siatkę dla graniastosłupa. Możliwe są inne siatki.

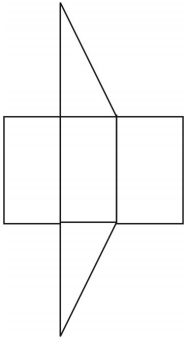
Ćwiczenia poglądowe

Narysuj siatkę dla każdego z poniższych:

Odpowiedzi

Pryzmy

Pryzmat to figura trójwymiarowa o parze równoległych i przystających do siebie końców, czyli podstaw. Boki graniastosłupa są równoległobokami. Pryzmaty są identyfikowane przez ich podstawy.

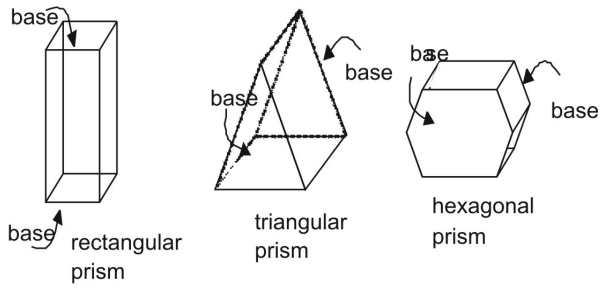
Surface Area of a Prism Using Nets

Pryzmaty powyżej są graniastosłupami prawymi. W graniastosłupie prawidłowym boczne ściany są prostopadłe do podstaw graniastosłupa. Porównaj graniastosłup prawidłowy z graniastosłupem skośnym, w którym boki i podstawy nie są prostopadłe.

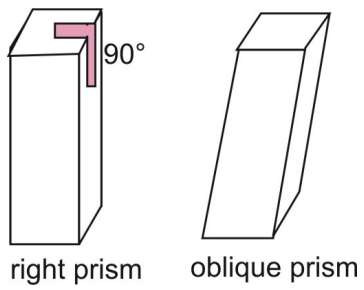
Dwa postulaty, które dotyczą powierzchni, to postulat spójności powierzchni i postulat dodawania powierzchni.

Postulat spójności powierzchni: Jeżeli dwa wielokąty (lub figury płaskie) są przystające, to ich powierzchnie są przystające.
Postulat dodawania powierzchni: Pole powierzchni figury trójwymiarowej jest sumą pól powierzchni wszystkich jej nienakładających się części.

Możesz użyć siatki i Postulatu Dodawania Powierzchni, aby znaleźć pole powierzchni graniastosłupa prawidłowego.

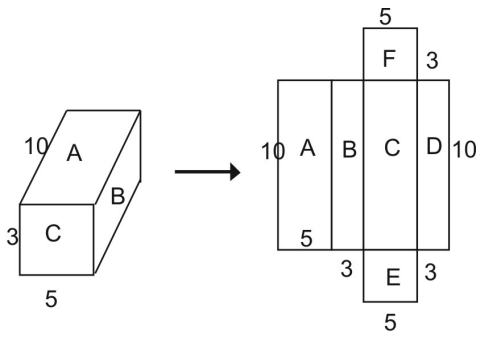
Z siatki widać, że pole powierzchni całego graniastosłupa jest równe sumie liczb tworzących siatkę:

Powierzchnia całkowita = pole powierzchni A + pole powierzchni B + pole powierzchni C + pole powierzchni D + pole powierzchni E + pole powierzchni F

Korzystając ze wzoru na pole powierzchni prostokąta widać, że pole powierzchni prostokąta A wynosi:

A = l – w
A = 10 – 5 = 50 jednostek kwadratowych

Podobnie, pola powierzchni pozostałych prostokątów wstawiamy z powrotem do powyższego równania.

Powierzchnia całkowita = pole A + pole B + pole C + pole D + pole E + pole F
Powierzchnia całkowita = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3) + (5 – 3)
Całkowite pole powierzchni = 50 + 30 + 50 + 30 + 15 + 15
Całkowite pole powierzchni = 190 jednostek kwadratowych

Przykład 3

Użyj siatki, aby znaleźć pole powierzchni graniastosłupa.

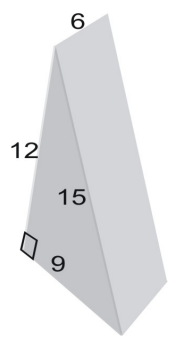
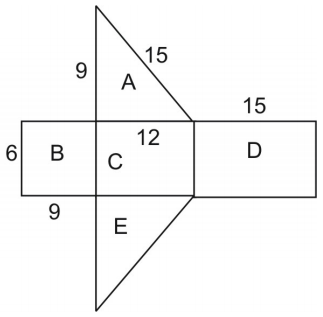
Pole powierzchni siatki jest równe polu powierzchni tej figury. Aby znaleźć pole trójkąta, korzystamy ze wzoru:

gdzie h to wysokość trójkąta, a b to jego podstawa.

Zauważ, że trójkąty A i E są przystające, więc możemy pomnożyć pole trójkąta A przez 2.

tekstylia}=tekstylia{area}A+tekstylia{area}B+tekstylia{area}C+tekstylia{area}D+tekstylia{area}E=2(tekstylia{area}A)+tekstylia{area}B+tekstylia{area} }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\

Thus, pole powierzchni wynosi 324 jednostki kwadratowe.

Ćwiczenia poglądowe

Dla każdego z poniższych znaleźć powierzchnię są a metodą siatek oraz obwód

  3. Podstawa graniastosłupa jest trójkątem prostokątnym, którego nogi mają długości 3 i 4, a wysokość jest równa 20. Jakie jest pole powierzchni całkowitej graniastosłupa?
  4. Pryzmat sześciokątny ma wysokość 24 cali i podstawy, które są sześciokątami foremnymi o boku 8 cali. Jakie jest pole powierzchni całkowitej?
  5. Jaka jest objętość graniastosłupa w problemie #4?

W poniższych pytaniach stodoła ma kształt graniastosłupa pięciokątnego o wymiarach podanych w stopach:

  1. Ile stóp kwadratowych (nie licząc dachu) znajduje się na powierzchni stodoły, która ma być pomalowana?
  2. Jeśli galon farby pokrywa 250 stóp kwadratowych, ile galonów farby potrzeba do pomalowania stodoły?
  3. Karton jest idealnym sześcianem o krawędzi mierzącej 17 cali. Ile stóp sześciennych może pomieścić?
  4. Basen ma 16 stóp szerokości, 32 stopy długości i jest równomiernie głęboki na 4 stopy. Ile stóp sześciennych wody może pomieścić?
  5. Pudełko po płatkach śniadaniowych ma długość 25 cm, szerokość 9 cm i wysokość 30 cm. Ile płatków może pomieścić?

Odpowiedzi

Siatki i obwód:

  1. 40,5 cala2
  2. 838 cm2
  3. 252 jednostki kwadratowe
  4. 1484.6 jednostek kwadratowych
  5. 3990,7 cali sześciennych

Stodoła:

  1. 2450 stóp kwadratowych
  2. 10 galonów farby
  3. 2,85 stóp sześciennych (tutaj należy być ostrożnym. Jednostki w problemie są podane w calach, ale pytanie pyta o stopy.)
  4. 2048 stóp sześciennych
  5. 6750 cm3

Cylindry

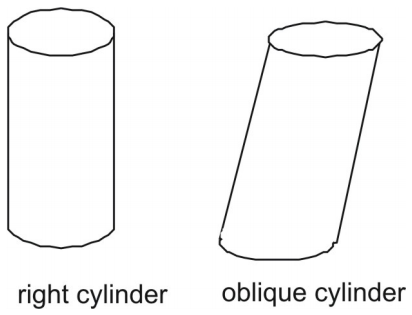
Cylinder jest figurą trójwymiarową z parą równoległych i przystających okrągłych końców, lub podstaw. Cylinder ma jeden zakrzywiony bok, który tworzy prostokąt, gdy jest położony płasko.

Tak jak w przypadku pryzmatów, cylindry mogą być proste lub skośne. Bok walca prawego jest prostopadły do jego okrągłych podstaw. Bok walca skośnego nie jest prostopadły do jego podstaw.

Powierzchnia walca przy użyciu siatek

Możesz rozłożyć walec na siatki.

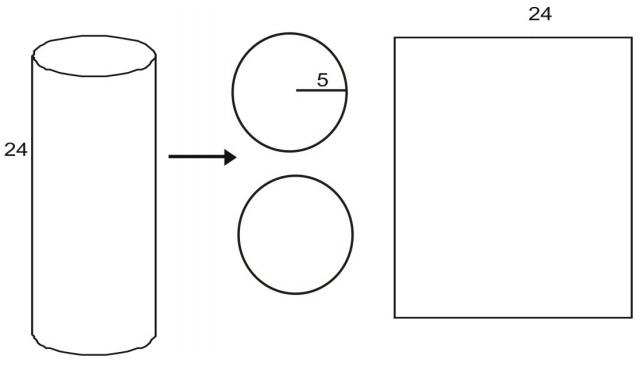
Obszar każdej podstawy jest dany przez pole koła:

A=pi{r}^2
A=pi(5)^2
A=25
A=approx(25)(3,14)=78,5

Pole powierzchni bocznej prostokąta L jest dane przez iloczyn szerokości i wysokości. Wysokość jest dana jako 24. Widać, że szerokość obszaru jest równa obwodowi okrągłej podstawy.

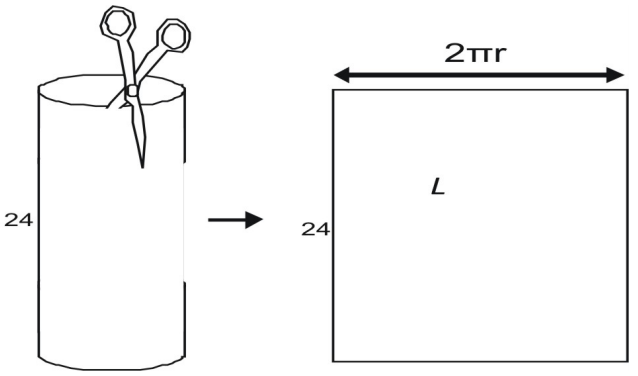
Aby znaleźć szerokość, wyobraź sobie, że rozbierasz nożyczkami walec przypominający puszkę. Po przecięciu powierzchni bocznej widzimy, że jest ona równa obwodowi wierzchołka puszki. Obwód koła jest dany przez C = 2πr, pole powierzchni bocznej, L, wynosi

L=2{pi}rh
L=2{pi}(5)(24)\(5)(24)\(3.14)=753,6>

Teraz możemy znaleźć pole powierzchni całego walca korzystając z zależności A = (pole powierzchni dwóch podstaw) + (pole powierzchni bocznej).

A=2(75,36)+753,6
A=904,32

Widzimy, że wzór, którego użyliśmy do znalezienia pola powierzchni całkowitej, możemy zastosować dla dowolnego walca prostego.

Pole powierzchni walca prostego: Pole powierzchni walca prostego o promieniu i wysokości h jest dane wzorem A = 2B + L, gdzie B jest polem każdej podstawy walca, a L jest polem powierzchni bocznej walca.

Przykład 4

Użyj siatki, aby znaleźć pole powierzchni walca.

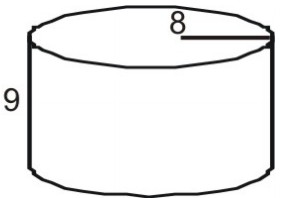
Najpierw narysuj i oznacz siatkę dla danej figury.

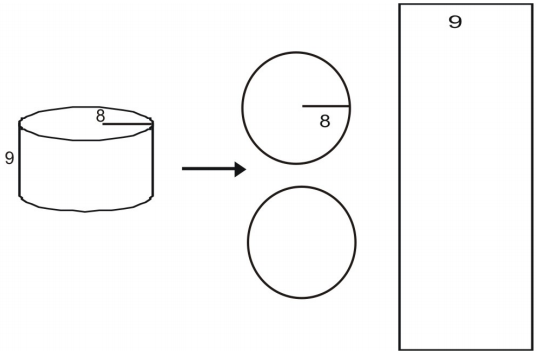
Oblicz pole powierzchni każdej podstawy.

A=pi{r}^2
A=pi(8)^2
A=64
A=approx(64)(3.14)=200.96\\

Calculate L.

L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16

Znajdź pole powierzchni całego walca.

A=2(200.96)+452.16
A=854.08 jednostek kwadratowych

W ten sposób powierzchnia całkowita wynosi około 854,08 jednostek kwadratowych

Powierzchnia walca z wykorzystaniem wzoru

Widziałeś, jak wykorzystać siatki do znalezienia powierzchni całkowitej walca. Postulat może być rozbity, aby stworzyć ogólny wzór dla wszystkich cylindrów prostych.

A = 2B + L

Zauważ, że podstawa, B, dowolnego walca wynosi: B = πr2

Powierzchnia boczna, L, dla dowolnego walca wynosi:

L= tekst{szerokość powierzchni bocznej}
L= tekst{obwód podstawy}
L=2pi{r}

Składając te dwa równania razem otrzymujemy:

Wykreślenie a z równania daje:

Powierzchnia walca prostego: Pole powierzchni walca prostego o promieniu r i wysokości h można wyrazić jako:

A = 2πr2 + 2πrh

lub:

A = 2πr(r + h)

W celu znalezienia pola powierzchni dowolnego walca prostego można skorzystać ze wzorów.

Przykład 5

Użyj wzoru, aby znaleźć pole powierzchni walca.

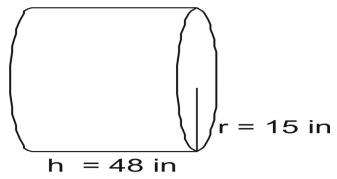
Zapisz wzór, podstaw wartości i rozwiąż.

A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6 cali kwadratowych}

Przykład 6

Znajdź pole powierzchni walca.

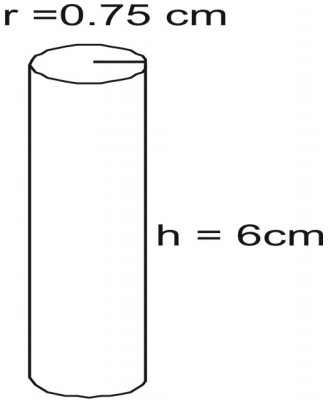
Napisz wzór i podstaw wartości i rozwiąż.

A=2pi{r}(r+h)\(r+h)\
A=2(3,14)(0,75)\
A=31.7925 cali kwadratowych}

Przykład 7

Znajdź wysokość walca, który ma promień 4cm i pole powierzchni 226,08 cm2.

Zapisz wzór korzystając z podanych informacji i rozwiąż dla h.

A=2pi{r}(r+h)

226,08=2(3,14)(4)
226,08=25,12
226,08=100,48+25,12h
5=h

Sfery

Sfera to figura trójwymiarowa, która ma kształt kuli.

Sfery można scharakteryzować na trzy sposoby.

  • Sfera to zbiór wszystkich punktów, które leżą w stałej odległości r od jednego punktu środkowego O.
  • Sfera to powierzchnia, która powstaje, gdy okrąg jest obracany wokół dowolnej ze swoich średnic.

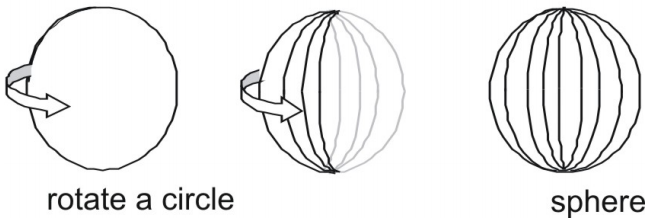
Powierzchnia kuli

Można wyprowadzić wzór na pole powierzchni kuli, wykonując pomiary kul i walców. Pokazujemy tu kulę o promieniu 3 i walec o promieniu i wysokości 3 oraz wyrażamy pole powierzchni w postaci π.

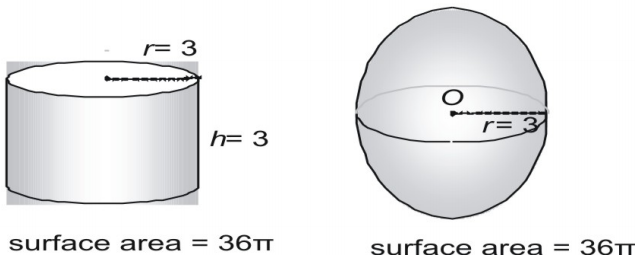
Teraz spróbujmy z większą parą, wyrażając pole powierzchni w postaci dziesiętnej.

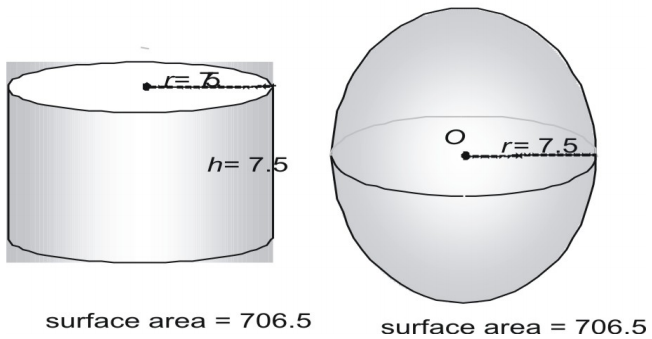
Spójrz na trzecią parę.

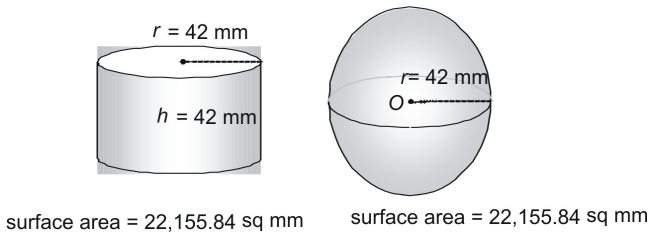
Czy to przypadek, że kula i walec, których promień i wysokość są równe promieniowi kuli, mają dokładnie takie samo pole powierzchni? Wcale nie! W rzeczywistości starożytni Grecy użyli metody, która pokazała, że następujący wzór może być użyty do znalezienia pola powierzchni dowolnej sfery (lub dowolnego cylindra, w którym ).

The Surface Area of a Sphere is given by: A = 4πr2

Przykład 8

Znajdź pole powierzchni kuli o promieniu 14 stóp.

Użyj wzoru.

A=4pi{r}^2
A=4pi(14)^2
A=4pi(196)^2
A=784
2461.76 stóp kwadratowych, wykorzystując 3,14 stopy kwadratowej do obliczenia pola powierzchni poniższej figury w funkcji π.

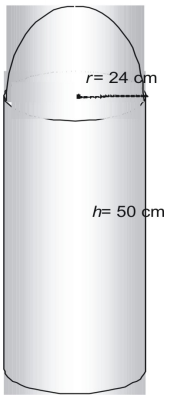
Figura jest zbudowana z jednej półkuli lub półkuli i jednego walca bez wierzchołka.

A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half kuli})=2 \pi(576)\
A(\pół kuli})=1152 \pkt cm}

Znajdź teraz pole powierzchni walca bez wierzchołka.

A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\

Thus, całkowita powierzchnia wynosi 1152\pi+2976\pi=4128\pi

Ćwiczenia poglądowe

  1. Znajdź promień kuli, która ma objętość 335 cm3.
  2. Określ pole powierzchni i objętość tego kształtu:
  3. Promień kuli wynosi 4. Znajdź jej objętość i pole powierzchni całkowitej.
  4. Kula ma promień 5. Prawy walec o tym samym promieniu ma taką samą objętość. Znajdź wysokość i pole powierzchni całkowitej walca.
  5. Sfera: objętość = 296 cm3. Znajdź średnicę.
  6. Sfera: pole powierzchni wynosi 179 in2. Znajdź promień.
  7. Piłki tenisowe o średnicy 3,5 cala są sprzedawane w puszkach po trzy sztuki. Puszka jest walcem. Przyjmij, że piłki dotykają puszki po bokach, na górze i na dole. Jaka jest objętość przestrzeni nie zajętej przez piłki tenisowe?
  8. Kula ma pole powierzchni 36π in2. Znajdź jej objętość.
  9. Gigantyczny czerpak, obsługiwany przez dźwig, ma kształt półkuli o promieniu = 21 cali. Czerpak jest wypełniony roztopioną, gorącą stalą. Gdy stal zostanie wlana do cylindrycznego zbiornika, który ma promień 28 cali, stopiona stal wzniesie się na wysokość ilu cali?

Odpowiedzi

Zauważ, że w tych zadaniach użyto π, a nie 3,14.

  1. 1. Promień = 4,31 cm
  2. Powierzchnia = 706,86 cm2
    Powierzchnia = 1767,15 cm3
  3. Pojemność = 268,08 jednostek3
    Powierzchnia = 201,06 jednostek2
  4. Wysokość = 20/3 jednostek powierzchnia całkowita = 366,52 jednostek2
  5. Średnica = 8,27cm
  6. Promień = 3.77 cali
  7. Pojemność cylindra = 32.16π in3 objętość piłek tenisowych = 21.44π in3
    Pojemność przestrzeni nie zajętej przez piłki tenisowe = 33.68 in3
  8. Pojemność = 113.10 in3
  9. Wysokość stopionej stali w cylindrze wyniesie 7.88 cali

.

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany.