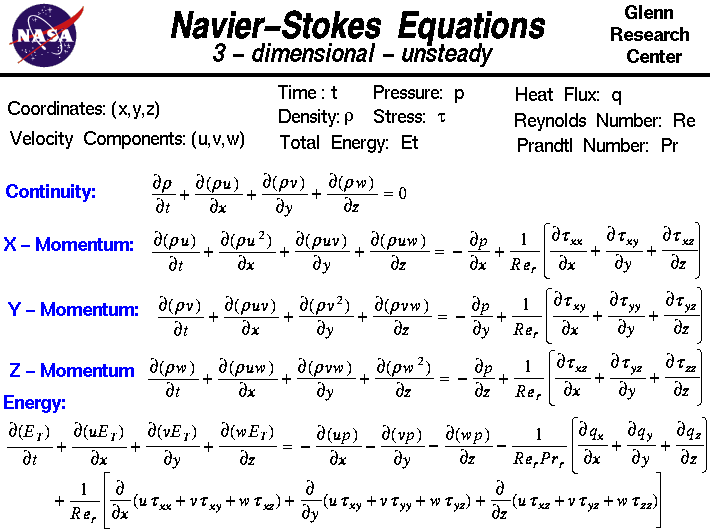
Na tym slajdzie pokazujemy trójwymiarową niestałą formę równań Naviera-Stokesa. Równania te opisują, w jaki sposób prędkość, ciśnienie, temperatura i gęstość poruszającej się cieczy są ze sobą powiązane. Równania te są rozszerzeniem równań Eulera i uwzględniają wpływ lepkości na przepływ. Równania te są bardzo złożone, ale studenci inżynierii uczą się jak je wyprowadzić w procesie bardzo podobnym do tego, który przedstawiamy na stronie o zachowaniu pędu.
Równania te są zbiorem sprzężonych równań różniczkowych i teoretycznie mogłyby być rozwiązane dla danego problemu z przepływem przy użyciu metod rachunku.Jednak w praktyce równania te są zbyt trudne do rozwiązania analitycznego.W przeszłości inżynierowie dokonywali dalszych przybliżeń i uproszczeń w zbiorze równań, aż do uzyskania grupy równań, które mogli rozwiązać.Ostatnio do rozwiązywania przybliżeń do równań używa się szybkich komputerów przy użyciu różnych technik, takich jak metoda różnic skończonych, metoda objętości skończonej, metoda elementów skończonych i metoda spektralna.Ten obszar badań nazywany jest obliczeniową dynamiką płynów lub CFD.
Równania Naviera-Stokesa składają się z zależnego od czasu równania ciągłości dla zachowania masy, trzech zależnych od czasu równań zachowania pędu oraz zależnego od czasu równania zachowania energii.W problemie występują cztery zmienne niezależne, współrzędne przestrzennex, y, i z pewnej domeny oraz czas t. Istnieje sześć zmiennych zależnych; współrzędne przestrzennex, y, i z pewnej domeny. Istnieje sześć zmiennych zależnych: ciśnienie p, gęstość r, temperatura T (która jest zawarta w równaniu energetycznym poprzez energię całkowitą Et) oraz trzy składowe wektora prędkości; składowa u jest w kierunku x, składowa v jest w kierunku y, a składowa w jest w kierunku z. Wszystkie zmienne zależne są funkcjami wszystkich czterech zmiennych niezależnych.Równania różniczkowe są zatem równaniami różniczkowymi cząstkowymi, a nie równaniami różniczkowymi zwyczajnymi, które studiujemy na początku zajęć z rachunku różniczkowego.
Zauważymy, że symbol różniczki jest inny niż zwykłe „d /dt” lub „d /dx”, które widzimy w przypadku równań różniczkowych zwyczajnych. Symbol „
” jest używany do wskazywania pochodnych cząstkowych. Symbol ten wskazuje, że podczas obliczania pochodnej mamy utrzymywać wszystkie zmienne niezależne na stałym poziomie, z wyjątkiem zmiennej obok symbolu. Zestaw równań jest następujący:
Ciągłość: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momentum: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = -. p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Momentum: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = -. p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momentum: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = -. p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energia: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
-. 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
gdzie Re jest liczbą Reynoldsa, która jest parametrem podobieństwa będącym stosunkiem skalowania bezwładności przepływu do sił lepkości w przepływie. Zmienne q są składowymi strumienia ciepła, a Pr jest liczbą Prandtla, która jest parametrem podobieństwa będącym stosunkiem naprężeń lepkich do naprężeń termicznych.Zmienne tau są składowymi tensora naprężeń.Tensor powstaje, gdy pomnożymy dwa wektory w określony sposób. Nasz wektor prędkości ma trzy składowe; tensor naprężeń ma dziewięć składowych. Każda składowa tensora naprężeń jest drugą pochodną składowych prędkości.
Wyrazy po lewej stronie równań pędu nazywane są wyrazami konwekcyjnymi równań.Konwekcja to proces fizyczny zachodzący w przepływie gazu, w którym pewna własność jest przenoszona przez uporządkowany ruch przepływu.Dyfuzja jest procesem fizycznym zachodzącym w przepływie gazu, w którym pewna właściwość jest transportowana przez przypadkowy ruch cząsteczek gazu. Dyfuzja jest związana z tensorem naprężeń i lepkością gazu. Turbulencja i powstawanie warstw granicznych są wynikiem dyfuzji w przepływie. Równania Eulera zawierają tylko konwekcyjne składniki równań Naviera-Stokesa i dlatego nie mogą modelować warstw granicznych. Istnieje specjalne uproszczenie równań Naviera-Stokesa, które opisują przepływy w warstwach granicznych.
Zauważ, że wszystkie zmienne zależne pojawiają się w każdym równaniu.Aby rozwiązać problem przepływu, musisz rozwiązać wszystkie pięć równań jednocześnie; dlatego nazywamy to sprzężonym układem równań.W rzeczywistości istnieje jeszcze kilka innych równań, które są wymagane do rozwiązania tego układu. Pokazujemy tylko pięć równań dla sześciu niewiadomych. Równanie stanu określa ciśnienie, temperaturę i gęstość gazu.Musimy również określić wszystkie warunki tensora naprężeń.W CFD warunki tensora naprężeń są często aproksymowane przez model turbulencji.
Działania:
Przewodniki:
Podróż
Strona główna przewodnika dla początkujących