Sun, 18 Jun 2006
1+1=2
Principia Mathematica Whiteheada i Russella jest znana z tego, że zajmuje tysiąc stron, by udowodnić, że 1+1=2. Oczywiście, udowadnia też wiele innych rzeczy. Gdyby chcieli udowodnić tylko to, że 1+1=2, prawdopodobnie zajęłoby to o połowę mniej miejsca.
Principia Mathematica to dziwna książka, warta obejrzenia zarówno z historycznego, jak i matematycznego punktu widzenia. Została napisana około 1910 roku, a logika matematyczna była wtedy jeszcze w powijakach, świeżo po transformacji dokonanej na niej przez Peano i Fregego. Notacja jest nieco niejasna, ponieważ od tego czasu notacja matematyczna znacznie się rozwinęła. Podobnie jak w źle napisanym programie komputerowym, duża część Principia Mathematica to powtórzony kod, oddzielne sekcje, które mówią zasadniczo o tym samym, ponieważ autorzy nie nauczyli się jeszcze technik, które pozwoliłyby połączyć te sekcje w jedną.
Na przykład, sekcja ∗22, „Obliczanie klas”, zaczyna się od zdefiniowania relacji podzbiorów (∗22.01), operacji łączenia i przecinania zbiorów (∗22.02 i .03), dopełnienia zbioru (∗22.04) i różnicy dwóch zbiorów (∗22.05). Następnie dowodzi komutatywności i asocjatywności związków zbiorów i przecięć zbiorów (∗22.51, .52, .57 i .7), różnych własności, takich jak !!! (∗22.5) i tym podobne, aż do twierdzeń takich jak ∗22.92: !!!∗alfa ∗podsetek ∗beta ∗prawa strzałka ∗alfa ∗cup(∗beta – ∗alfa)!!.
Sekcja ∗23 jest „Obliczaniem relacji” i zaczyna się prawie dokładnie w ten sam sposób, definiując relację podrelacji (∗23.01), operacje łączenia i przecinania relacji (∗23.02 i .03), dopełnienie relacji (∗23.04) i różnicę dwóch relacji (∗23.05). Udowadnia komutatywność i asocjatywność związków i przecięć relacji (∗23.51, .52, .57 i .7), różne własności, takie jak !!alfa = alfa!!! (∗22.5) i tym podobne, aż do twierdzeń takich jak ∗23.92: !!!alfa ∗dot ∗subset ∗beta ∗rightarrow ∗dot ∗cup(∗beta ∗dot-alfa)!!.
Dział ∗24 dotyczy istnienia zbiorów, zbioru zerowego !!!∗Lambda!!!, zbioru uniwersalnego !!!∗ V}!!!Ich własności i tak dalej, a następnie sekcja ∗24 jest powielona w ∗25 w serii twierdzeń o istnieniu relacji, relacji zerowej !!!, relacji uniwersalnej !!!, ich własności i tak dalej.
Tak to zrobili Whitehead i Russell w 1910 roku. Jak zrobilibyśmy to dzisiaj? Relacja między S i T jest zdefiniowana jako podzbiórS × T, a zatem jest zbiorem. Unia, przecięcie, różnica i inne operacje są dokładnie takie same dla relacji, jak dla zbiorów, ponieważ relacje są zbiorami. Wszystkie twierdzenia o związkach i przecięciach relacji, jak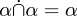 
, po prostu odchodzą, ponieważ już udowodniliśmy je dla zbiorów, a relacje są zbiorami. Relacja zerowa jest zbiorem zerowym. The universal relation ishe universal set.
Ogromna ilość innych maszyn odchodzi w 2006 roku, z powodu unifikacji relacji i zbiorów. Principia Mathematica potrzebuje specjalnej notacji i specjalnej definicji dla wyniku ograniczenia relacji do tych par, których pierwszy element jest członkiem danego zbioru S, lub których drugi element jest członkiem S, lub których oba elementy są członkami S; w 2006 roku po prostu użylibyśmy zwykłej operacji przecięcia zbiorów i mówilibyśmy o R ∩(S×B) lub cokolwiek innego.
Whitehead i Russell nie mogli tego zrobić w 1910 roku, ponieważ brakowało kluczowego elementu maszynerii: pary uporządkowanej. W 1910 roku nikt nie wiedział, jak zbudować parę uporządkowaną z samej logiki i zbiorów. W roku 2006 (lub nawet 1956) zdefiniowalibyśmy parę uporządkowaną <a, b> jako zbiór {{a}, {a, b}}. Następnie pokazalibyśmy jako twierdzenie, że <a, b> = <c, d> wtedy i tylko wtedy, gdy a=c i b=d, używając własności zbiorów. Następnie zdefiniowalibyśmy A×B jako zbiór wszystkich p takich, że p = <a,b> ∧ a ∈ A ∧ b∈ B. Następnie zdefiniowalibyśmy relację na zbiorachA i B jako podzbiór A×B. Wtedy dostalibyśmy wszystkie ∗23 i ∗25 oraz wiele z ∗33 i ∗35 i ∗36 za darmo, i prawdopodobnie także wiele innych rzeczy.
(Przy okazji, {{a}, {a, b}} rzecz została wymyślona przez Kuratowskiego. Zwykle przypisuje się to Norbertowi Wienerowi, ale pomysł Wienera, choć podobny, był w rzeczywistości bardziej skomplikowany.)
W Principia Mathematica nie ma uporządkowanych par, chyba że w sposób dorozumiany. Nie ma nawet prawie żadnych zbiorów. Whitehead i Russell chcą oprzeć wszystko na logice. Dla Whiteheada i Russella podstawowym pojęciem jest „funkcja propozycjonalna”, czyli funkcja φ, której wyjściem jest wartość prawdy. Dla każdej takiej funkcji istnieje odpowiadający jej zbiór, który oznaczają oni przez !!!, zbiór wszystkich x takich, że φ(x) jest prawdziwe. Dla Whiteheada i Russella, arelacja jest implikowana przez funkcję propozycjonalną dwóch zmiennych, analogicznie do tego, jak zbiór jest implikowany przez funkcję propozycjonalną jednej zmiennej. W 2006 roku pozbywamy się „funkcji dwóch zmiennych” i mówimy po prostu o funkcjach, których (pojedynczym) argumentem jest para uporządkowana; relacja staje się wtedy zbiorem wszystkich par uporządkowanych, dla których funkcja jest prawdziwa.
Russell miał podobno powiedzieć, że odkrycie skoku Sheffera (pojedynczego operatora logicznego, z którego można zbudować wszystkie inne operatory logiczne) było ogromnym postępem i zmieni wszystko. Teraz wydaje nam się to dziwne, bo odkrycie skoku Sheffera wydaje się takie proste, a tak naprawdę nie zmienia niczego istotnego. Wystarczy dodać na początku rozdziału 1 notatkę, że ∼p i p∨q są skrótami odpowiednio od p|p i p|p.|.q|q, udowodnić pięć podstawowych aksjomatów i pozostawić wszystko inne bez zmian. Ale Russell mógłby, z pewną dozą sprawiedliwości, powiedzieć to samo o odkryciu, że pary uporządkowane można interpretować jako zbiory, prostym odkryciu, które naprawdę przekształciłoby Principia Mathematica w całkiem inne dzieło.
W każdym razie, mając to tło na miejscu, możemy omówić dowód z Principia Mathematica, że 1+1=2. Występuje on dość późno w Principia Mathematica, w sekcji ∗102. Moja skrócona wersja sięga tylko do ∗56, ale to wystarczająco daleko, aby dotrzeć do ważnego twierdzenia prekursora, ∗54.43, zeskanowanego poniżej:
Notacja może być przytłaczająca, więc skupmy się tylko na stwierdzeniu twierdzenia, ignorując wszystko inne, nawet pomocną uwagę na dole:
To jest twierdzenie, które jest udowadniane; to, co następuje, jest dowodem.
Teraz powinienem wyjaśnić notację, która zmieniła się nieco od 1910 roku. Po pierwsze, Principia Mathematica używa notacji „kropek” Peano do dezambiguacjieprecedencji, gdzie teraz używamy nawiasów zamiast. Notacja kropkowa wymaga przyzwyczajenia się, ale ma pewne wyraźne zalety w porównaniu z nawiasami. Idea jest taka, że wskazujesz na grupowanie przez stawianie kropek, więc (1+2)×(3+4)×(5+6) jest zapisane jako1+2.×.3+4.×.5+6. Środkowa podformuła jest pomiędzy parą kropek. Podformuła (1+2) również znajduje się między parą kropek, ale kropka na lewym końcu jest zbędna, więc ją pomijamy; podobnie podformuła (5+6) jest ograniczona kropką po lewej i końcem formuły po prawej stronie.
A co jeśli musisz zagnieździć nawiasy? Wtedy używasz więcej kropek. Podwójna kropka (:) jest jak pojedyncza kropka, ale mocniejsza. Na przykład, wewrite ((1+2)×3)+4 jako 1+2 . × 3 : + 4, a podwójna kropka izoluje całe wyrażenie 1+2 . × 3 do pojedynczej podformuły, do której odnosi się +4.
Czasami potrzebujesz więcej poziomów pierwszeństwa, i wtedy używasz potrójnych kropek (.: i :.) i poczwórnych (::). Ta formuła, jak widzisz, ma podwójne i potrójne kropki. Przekładając kropki na standardową notację parentezy, mamy $$ast54.43. \((\alfa, \beta \ w 1 ) \supset (( \alpha \beta = \Lambda) \equiv (\alpha \cup \beta \ w 2)))$$. Wygląda to raczej bardziej nieporządnie niż wersja z kropkami, a przy nieskomplikowanych formułach możesz mieć problem z ustaleniem, które nawiasy pasują do których. Z kropkami, to zawsze jest łatwe. Myślę więc, że to trochę niefortunne, że ta konwencja wyszła z użycia.
Symbol !!∑vdash!! nie uległ zmianie; oznacza on, że formuła, do której ma zastosowanie, jest prawdziwa. !!∑supset!! to implikacja logiczna, a !!∑equiv!! to równoważność logiczna. Λ to zbiór pusty, który obecnie zapisujemy jako ∅. ∩ ∪ i ∈ mają swoje współczesne znaczenia: ∩ i ∪ to operatory przecięcia zbiorów i unii, a x∈y oznacza, że x jest elementem zbioru y.
Pozostałe punkty są semantyczne. α i β to zbiory. 1 oznacza zbiór wszystkich zbiorów, które mają dokładnie jeden element. To znaczy, że jest to zbiór { c : istnieje a takie, że c = {a } }. Do twierdzeń o 1 należą na przykład:
- że Λ∉1 (∗52.21),
- że jeśli α∈1 to istnieje jakieś x takie, że α ={x} (∗52.1), oraz
- że {x}∈1 (∗52.22).
2 jest podobnie zbiorem wszystkich zbiorów, które mają dokładnie dwa elementy. Ważnym twierdzeniem o 2 jest ∗54.3, które mówi, że $$ast54.3. ∗54.3. 2 = ∗ alfa ∗{ (∗ istnieje x) ∗ .∗x ∗ alfa ∗ . \
Twierdzi ono, że jeśli zbiory α i β mają dokładnie po jednym elemencie, to są one rozłączne (czyli nie mają elementów wspólnych) wtedy i tylko wtedy, gdy ich unia ma dokładnie dwa elementy.
Dowód, który pojawia się w powyższym skanie po słowie „Dem.” (skrót od „demonstracja”) brzmi następująco:
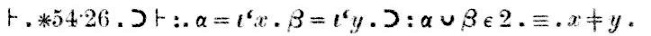
„Twierdzenie ∗54.26 implikuje, że jeśli α = {x} i β = {y}, toα∪β ma 2 elementy wtedy i tylko wtedy, gdy x jest różne od y.”
„Przez twierdzenie ∗51.231, ten ostatni bit (x jest różny ody) jest prawdziwy wtedy i tylko wtedy, gdy {x} i {y} sądisjoint.”
„By ∗13.12, this last bit ({x} and {y} are disjoint) istrue if and only if α and β themselves are disjoint.” Wniosek cząstkowy w tym punkcie,który jest oznaczony (1), jest taki, że jeśli α = {x} i β ={y}, to α∪β ∈ 2 wtedy i tylko wtedy, gdyα∩β = Λ.
Dowód kontynuuje: „Wniosek (1), z twierdzeniami ∗11.11 i ∗11.35,implikuje, że jeśli istnieją x i y tak, że α jest{x} i β jest {y}, to α∪β ∈ 2 wtedy i tylko wtedy, gdy α i β są rozłączne.” Ten wniosek jest oznaczony jako (2).
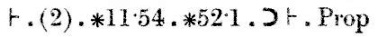
Wreszcie, wniosek (2), wraz z twierdzeniami ∗11.54 i ∗52.1, implikuje twierdzenie, które próbowaliśmy udowodnić.∗54.26, od którego to twierdzenie w dużej mierze zależy, jest prawie takie samo; stwierdza, że {x}∪{y} ∈ 2 wtedy i tylko wtedy, gdy x≠y. Z kolei ∗54.26 zależy od ∗54.101, który mówi, że α ma 2 elementy wtedy i tylko wtedy, gdy istnieją x i y, nie takie same, takie, że α = {x} ∪{y}. Twierdzenie ∗54.101 jest tylko trochę inne niż definicja 2. Twierdzenie ∗51.231 mówi, że {x} i {y} są rozłączne wtedy i tylko wtedy, gdy x i y są różne.∗52.1 jest podstawową własnością 1; widzieliśmy to już wcześniej.
Pozostałe twierdzenia przytoczone w demonstracji są bardzo drobnymi technicznymi zagadnieniami. Twierdzenie ∗11.54 mówi, że można wziąć twierdzenie o istnieniu dwóch rzeczy i rozdzielić je na dwa twierdzenia, z których każde twierdzi, że jedna z tych rzeczy istnieje. ∗11.11 jest jeszcze szczuplejszy: mówi, że jeśli φ(x, y) jest zawsze prawdziwe, to można dołączyć kwantyfikator uniwersalny i twierdzić, że φ(x, y) jest prawdziwe dla wszystkich x i y. ∗13.12 dotyczy zamiany równych na równych: jeśli x i y są takie same, to x posiada własność ψ wtedy i tylko wtedy, gdy y również ją posiada.
Nie widziałem późniejszych części Principia Mathematica, ponieważ moja kopia kończy się po rozdziale ∗56, a arytmetyka jest znacznie późniejsza. Ale to twierdzenie wyraźnie ma w sobie sens 1+1=2, a późniejsze twierdzenie (∗110.643), które faktycznie stwierdza 1+1=2, silnie zależy od tego twierdzenia.
Ale nie jestem całkowicie pewien, co się stanie później (zmarnowałem już na to o wiele za dużo czasu, żeby włożyć więcej czasu w pełną wersję z biblioteki), mogę zgadywać. Principia Mathematica będzie definiować liczbę 17 jako zbiór wszystkich 17-elementowych zbiorów, i podobnie każdą inną liczbę; użycie symbolu 2 do reprezentowania zbioru wszystkich 2-elementowych zbiorów zapowiada to. Thesesets of-all-sets-of-a-certain-size will then be identified as the „cardinal numbers”.
W Principia Mathematica zdefiniujemy sumę liczb kardynalnych p i q w następujący sposób: weź zbiór reprezentatywny a z p; a ma p elementów. Weźmy zbiór reprezentatywny b z q; b ma q elementów. Niech c =a∪b. Jeśli c jest członkiem pewnej liczby kardynalnej r, i jeśli a i b są rozłączne, to suma p i q jest r.
Z tą definicją można udowodnić zwykłe pożądane własności dodawania, takie jak x + 0 = x, x + y = y + x, i 1 + 1 = 2.
W szczególności, 1+1=2 wynika bezpośrednio z twierdzenia ∗54.43; jest to dokładnie to, czego chcemy, ponieważ aby obliczyć 1+1, musimy znaleźć dwa rozłączne reprezentanty 1 i wziąć ich unię; ∗54.43 twierdzi, że unia musi być elementem 2, niezależnie od tego, którego reprezentanta wybierzemy, więc 1+1=2.
Post scriptum: Peter Norvig mówi, że circumflex w notacji Principia Mathematica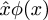 
jest ostatecznym źródłem użycia słowa lambda do oznaczenia anonimowej funkcji w językach programowania Lisp i Python. Jestem pewien, że wiesz, że te języki dostają „lambda” od użycia greckiej litery λ przez Alonzo Churcha do reprezentowania abstrakcji funkcji w jego „λ-calculus”: W Lisp,(lambda (u) B) jest funkcją, która przyjmuje argumentu i zwraca wartość B; w λ-calculus,λu.B jest funkcją, która przyjmuje argumentu i zwraca wartość B. Norvig mówi, że Church pierwotnie planował napisać funkcjęλu.B jako û.B, ale jego drukarka nie mogła zrobić akcentów circumflex. Rozważał więc przesunięcie akcentu okalającego w lewo i użycie zamiast niego wielkiej litery lambda: Λu.B. Wielkie Λ wyglądało zbyt podobnie do ∧ i ∧, co było mylące, więc zamiast tego użył małej litery lambdaλ.
Post post scriptum: Wszyscy zawsze mówią „Russell i Whitehead”.Wyniki Google dla „Russell i Whitehead” przewyższają te dla „Whitehead i Russell” o dwa do jednego, na przykład. Dlaczego? Na okładce i na stronie tytułowej jest napisane „Alfred North Whitehead i Bertrand Russell, F.R.S.”. Jak i kiedy Whitehead stracił pierwszeństwo?
stały link
.