Warstwa graniczna jest cienką warstwą lepkiego płynu blisko stałej powierzchni ściany stykającej się z poruszającym się strumieniem, w której (w ramach jej grubości δ) prędkość przepływu zmienia się od zera przy ścianie (gdzie przepływ „przykleja się” do ściany z powodu swojej lepkości) do Ue na granicy, co w przybliżeniu (z błędem 1%) odpowiada prędkości swobodnego strumienia (patrz rys. 1). Ściśle mówiąc, wartość δ jest wartością arbitralną, ponieważ siła tarcia, zależna od oddziaływań molekularnych pomiędzy płynem a ciałem stałym, maleje wraz z odległością od ściany i staje się równa zeru w nieskończoności.
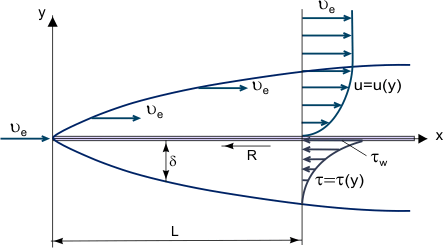
Rysunek 1. Wzrost warstwy granicznej na płaskiej płycie.
Podstawowe pojęcie warstwy granicznej zaproponował L. Prandtl (1904), definiuje on warstwę graniczną jako warstwę płynu rozwijającą się w przepływach o bardzo dużych liczbach Reynoldsa Re, czyli o stosunkowo małej lepkości w porównaniu z siłami bezwładności. Zjawisko to obserwuje się, gdy ciała wystawione są na działanie strumienia powietrza o dużej prędkości lub gdy ciała są bardzo duże, a prędkość strumienia powietrza jest umiarkowana. W tym przypadku, w stosunkowo cienkiej warstwie granicznej, naprężenie ścinające tarcia (lepka siła ścinająca): τ = η (gdzie η jest lepkością dynamiczną; u = u(y) – „profil” składowej podłużnej prędkości warstwy granicznej, patrz rys. 1) może być bardzo duże; w szczególności przy ścianie, gdzie u = 0 i τw = ηw, chociaż sama lepkość może być raczej mała.
Można pominąć siły tarcia poza warstwą graniczną (w porównaniu z siłami bezwładności) i na podstawie koncepcji Prandtla rozważyć dwa rejony przepływu: warstwę graniczną, w której efekty tarcia są duże i rdzeń przepływu prawie inviscid. Przy założeniu, że warstwa graniczna jest warstwą bardzo cienką (δ << L, gdzie L jest charakterystycznym wymiarem liniowym ciała, nad którym występuje przepływ lub kanału zawierającego przepływ, jej grubość maleje ze wzrostem Re, rys. 1), można oszacować rząd wielkości grubości warstwy granicznej z następującej zależności:
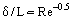
Na przykład, gdy samolot leci z prędkością Ue = 400 km/godz, grubość warstwy granicznej na krawędzi spływu skrzydła o cięciwie (długości profilu) 1 metra wynosi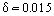 m. Jak stwierdzono doświadczalnie, w części wlotowej do korpusu rozwija się laminarna warstwa graniczna. Stopniowo, pod wpływem pewnych czynników destabilizujących, warstwa graniczna staje się niestabilna i następuje przejście warstwy granicznej do reżimu przepływu turbulentnego. Specjalne badania doświadczalne wykazały istnienie obszaru przejściowego pomiędzy obszarem turbulentnym a laminarnym. W niektórych przypadkach (na przykład, przy wysokim poziomie turbulencji przepływu zewnętrznego), warstwa graniczna staje się turbulentna bezpośrednio za punktem stagnacji przepływu. W pewnych warunkach, takich jak silny spadek ciśnienia, w przyspieszających przepływach turbulentnych zachodzi odwrotne zjawisko, a mianowicie relaminaryzacja przepływu.
m. Jak stwierdzono doświadczalnie, w części wlotowej do korpusu rozwija się laminarna warstwa graniczna. Stopniowo, pod wpływem pewnych czynników destabilizujących, warstwa graniczna staje się niestabilna i następuje przejście warstwy granicznej do reżimu przepływu turbulentnego. Specjalne badania doświadczalne wykazały istnienie obszaru przejściowego pomiędzy obszarem turbulentnym a laminarnym. W niektórych przypadkach (na przykład, przy wysokim poziomie turbulencji przepływu zewnętrznego), warstwa graniczna staje się turbulentna bezpośrednio za punktem stagnacji przepływu. W pewnych warunkach, takich jak silny spadek ciśnienia, w przyspieszających przepływach turbulentnych zachodzi odwrotne zjawisko, a mianowicie relaminaryzacja przepływu.
Pomimo swojej względnej cienkości, warstwa graniczna jest bardzo ważna dla inicjowania procesów dynamicznej interakcji pomiędzy przepływem a ciałem. Warstwa graniczna określa opór aerodynamiczny i uniesienie pojazdu latającego, lub straty energii dla przepływu cieczy w kanałach (w tym przypadku, hydrodynamiczna warstwa graniczna, ponieważ istnieje również termiczna warstwa graniczna, która określa termodynamiczną interakcję wymiany ciepła).
Obliczanie parametrów warstwy granicznej opiera się na rozwiązaniu równań otrzymanych z równań Naviera-Stokesa dla ruchu płynu lepkiego, które najpierw są znacznie uproszczone biorąc pod uwagę cienkość warstwy granicznej.
Rozwiązanie zaproponowane przez L. Prandtla jest w istocie pierwszym członem rozwinięcia szeregu potęgowego równania Naviera-Stokesa, przy czym rozwinięcie szeregu następuje dla potęg bezwymiarowego parametru (δ/L). Mniejszy parametr w tym wyrażeniu jest w potędze zerowej, tak że równanie warstwy granicznej jest przybliżeniem zerowym w asymptotycznym rozwinięciu (przy dużym Re) równania warstwy granicznej (rozwiązanie asymptotyczne).
Przekształcenie równania Naviera-Stokesa w równania warstwy granicznej można zademonstrować wyprowadzając równanie Prandtla dla laminarnej warstwy granicznej w dwuwymiarowym nieściśliwym przepływie bez sił od ciała.
W tym przypadku układ równań Naviera-Stokesa będzie miał postać:

Po oszacowaniu rzędu wielkości niektórych członów równania Eq. (2) i pominięciu małych członów układ równań Prandtla dla laminarnej warstwy granicznej przyjmuje postać:

w którym x, y są współrzędnymi podłużną i poprzeczną (rysunek 1); v jest składową prędkości wzdłuż osi „y”; p, ciśnienie; t, czas; i n lepkość kinematyczna.
Warstwa graniczna jest cienka i prędkość na jej zewnętrznej krawędzi Ue może być wystarczająco i dokładnie określona jako prędkość idealnego (indykującego) przepływu płynu wzdłuż ściany obliczona do pierwszego przybliżenia, bez uwzględnienia odwrotnego działania warstwy granicznej na przepływ zewnętrzny. Wzdłużny gradient ciśnienia = (przy p(y) = const) w równaniu (3) może być przedstawiony na podstawie równania ruchu Eulera płynu idealnego. Z powyższego wynika, że równania Prandtla w postaci skończonej zapiszemy jako:

Jest to układ parabolicznych, nieliniowych równań różniczkowych cząstkowych drugiego rzędu, które są rozwiązywane z warunkami początkowymi i brzegowymi


Układ równań (4) jest zapisany dla rzeczywistych wartości składowych prędkości u i v. Aby uogólnić otrzymane równania dla przepływu turbulentnego należy wykorzystać dobrze znane zależności pomiędzy składowymi rzeczywistymi, uśrednionymi i pulsującymi parametrów przepływu turbulentnego. Na przykład, dla składowych prędkości istnieją zależności łączące składowe rzeczywiste u i v, uśrednione ū i oraz pulsujące u’ i v’:
oraz pulsujące u’ i v’:

Po pewnych przearanżowaniach można z układu (3) otrzymać inny układ równań, w szczególności dla przepływu ustalonego:
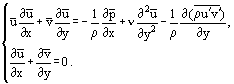
Używając następującej zależności dla naprężeń ścinających tarcia w warstwie granicznej:
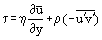
oraz biorąc pod uwagę, że w laminarnej warstwie granicznej u = u’ i można przepisać równania Prandtla w postaci obowiązującej zarówno dla przepływów laminarnych jak i turbulentnych:
można przepisać równania Prandtla w postaci obowiązującej zarówno dla przepływów laminarnych jak i turbulentnych:
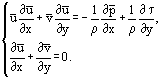
Najprostsze rozwiązania otrzymano dla laminarnej warstwy granicznej na cienkiej płaskiej płycie w dwuwymiarowym, równoległym przepływie nieściśliwego płynu (rys. 1). W tym przypadku oszacowanie rzędu wielkości członów równań: x ~ L, y ~ δ, δ ~ pozwala połączyć zmienne x i y w jednej relacji
pozwala połączyć zmienne x i y w jednej relacji

i sprowadzić rozwiązanie równania (8) (przy dp/dx = 0) do wyznaczenia zależności u i v od nowego parametru ξ. Z drugiej strony, wykorzystując znane zależności pomiędzy składowymi prędkości u, v i funkcją strumienia ψ

można otrzymać jedno równanie różniczkowe zwyczajne nieliniowe trzeciego rzędu, zamiast układu równań różniczkowych cząstkowych (8)

Tutaj f(ξ) jest nieznaną funkcją zmiennej ξ: f = ƒ =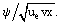
Pierwsze rozwiązanie numeryczne równania Eq. (10) zostało otrzymane przez Blasiusa (1908) w warunkach brzegowych odpowiadających warunkom fizycznym warstwy brzegowej przy y = 0: u = 0, v = 0; przy y → ∞; u → Ue (Blasius boundary layer).
Rysunek 2 porównuje wyniki rozwiązania Blasiusa (linia ciągła) z danymi eksperymentalnymi. Na podstawie tych danych można oszacować grubość lepkiej warstwy granicznej. Przy ξ  2.5, (u/Ue
2.5, (u/Ue 0.99) (Rysunek 2); w konsekwencji z równania (9) otrzymujemy:
0.99) (Rysunek 2); w konsekwencji z równania (9) otrzymujemy:

Rysunek 2.
Z obliczeń numerycznych Blasiusa wartości drugiej pochodnej funkcji f(ξ) przy naprężeniu ścinającym tarcie przyścienne, zależność w tym przypadku wynosi:

Siłę tarcia R, działającą po obu stronach płyty o długości L (rys. 1), wyznaczamy również z Eq. (11):

jak w przypadku współczynnika tarcia dla płyt płaskich:
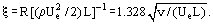
Mimo, że równania Prandtla są znacznie prostsze od równań Naviera-Stokesa, ich rozwiązania otrzymano dla ograniczonej liczby problemów. Dla wielu praktycznych problemów nie jest konieczne wyznaczanie profili prędkości w warstwie granicznej, a jedynie grubości i naprężenia ścinającego. Tego typu informacje można uzyskać rozwiązując całkowe równanie pędu

Zależność całkowa (12) obowiązuje zarówno dla laminarnej jak i turbulentnej warstwy granicznej.
Wyniki, które nie były znane a priori, a które charakteryzują rozkład parametrów płynu w całej grubości warstwy δ są objęte całką w równaniu (12). A błąd obliczenia tej całki jest mniejszy niż błąd w przybliżeniu przyjętej funkcji całkującej ρu = ρu(y). Stwarza to warunki do opracowania przybliżonych metod obliczania parametrów warstwy brzegowej, które są mniej czasochłonne niż dokładne metody całkowania równań Prandtla. Fundamentalna koncepcja została po raz pierwszy zaproponowana przez T. von Karmana, który wprowadził taką arbitralną grubość warstwy δ*
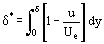
i grubość przesunięcia pędu δ**
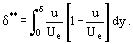
, dzięki czemu możemy przekształcić Eq. (12) dla dwuwymiarowej warstwy granicznej płynu nieściśliwego na:

W równaniu (15) występują trzy niewiadome, mianowicie δ* = δ*(x), δ** = δ**(x) i τw = τw(x) .
Rozwiązanie równania różniczkowego zwyczajnego, takiego jak Eq. (15) zwykle wymaga założenia (lub przedstawienia) rozkładu prędkości (profilu prędkości) w całej grubości warstwy granicznej jako funkcji pewnych charakterystycznych parametrów (form-parametrów), a także wymaga użycia danych empirycznych o związku pomiędzy współczynnikiem tarcia Cf = 2τw/(ρU2e) i dowolną grubością warstwy granicznej (prawo tarcia).
Pewne definitywne wyjaśnienia fizyczne mogą być podane, jeśli chodzi o wartości δ* i δ**. Funkcja całkująca w równaniu (13) zawiera po przekształceniu człon (Ue – u), który charakteryzuje spadek prędkości. Całka z równania (14) może być więc traktowana jako miara zmniejszenia prędkości przepływu przez warstwę graniczną w porównaniu z przepływem idealnym przy prędkości Ue. Z drugiej strony, wartość δ* może być traktowana jako miara odchylenia wzdłuż normalnej do ściany (wzdłuż osi „y”) linii strumienia przepływu zewnętrznego pod wpływem sił tarcia. Z rozważań nad całkową strukturą równania (14) można wywnioskować, że δ** charakteryzuje spadek pędu w warstwie granicznej pod wpływem tarcia.
Ważne są następujące zależności:

gdzie H jest parametrem postaci profilu prędkości warstwy granicznej. Na przykład, dla rozkładu liniowego u = ky,
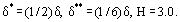
Obecnie do przewidywania parametrów turbulentnej warstwy granicznej powszechnie stosuje się tzw. teorie półempiryczne. W tym przypadku zakłada się, że całkowite naprężenie tarcia τ w turbulentnej warstwie granicznej jest sumą

Tutaj τT jest dodatkowym (turbulentnym lub Reynoldsa) naprężeniem tarcia, w szczególności w przepływie nieściśliwym patrz Eq. (7).
patrz Eq. (7).
Ta reprezentacja jest bezpośrednio związana z układem równań ruchu w warstwie granicznej (6). W ściśliwej warstwie granicznej pulsacje gęstości mogą być uważane za wynik pulsacji temperatury

gdzie β = (1/T) jest współczynnikiem rozszerzalności objętościowej.
Dodatkowe półempiryczne hipotezy o turbulentnym przenoszeniu pędu są używane do określenia τT. Na przykład,

gdzie ηT jest dynamicznym współczynnikiem lepkości turbulentnej wprowadzonym przez J. Boussinesqa w 1877 r.
Na podstawie koncepcji podobieństwa wymiany molekularnej i turbulentnej (teoria podobieństwa) Prandtl wprowadził hipotezę długości mieszania (die Mischungsweg). Długość mieszania 1 jest to droga, jaką skończona objętość płynu („mol”) przechodzi z jednej warstwy o ruchu średnim do drugiej bez zmiany swojego pędu. Zgodnie z tym warunkiem wyprowadził równanie, które okazało się fundamentalne dla teorii warstw granicznych:

Dla turbulentnego regionu warstwy granicznej przepływu przyściennego, L. Prandtl uważał długość 1 proporcjonalną do y

gdzie κ jest stałą empiryczną.
Bliżej ściany, gdzie ηT << η, czynnikiem decydującym jest lepkie tarcie molekularne. Grubość tej części warstwy granicznej δ1, którą nazywamy podwarstwą laminarną lub lepką, wynosi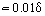 . Na zewnątrz podwarstwy wartość ηT wzrasta, osiągając kilka rzędów wielkości większą od η. Odpowiednio, w tej strefie warstwy granicznej zwanej rdzeniem turbulentnym τT > 0 = η. Czasami rdzeń turbulentny dzieli się na strefę buforową, w której tarcie laminarne i turbulentne mają porównywalną wartość, oraz strefę rozwiniętą, w której τT >> τ0. Dla tego regionu, po całkowaniu równania (18) i uwzględnieniu równania (19), można wyprowadzić wyrażenie na logarytmiczny profil prędkości:
. Na zewnątrz podwarstwy wartość ηT wzrasta, osiągając kilka rzędów wielkości większą od η. Odpowiednio, w tej strefie warstwy granicznej zwanej rdzeniem turbulentnym τT > 0 = η. Czasami rdzeń turbulentny dzieli się na strefę buforową, w której tarcie laminarne i turbulentne mają porównywalną wartość, oraz strefę rozwiniętą, w której τT >> τ0. Dla tego regionu, po całkowaniu równania (18) i uwzględnieniu równania (19), można wyprowadzić wyrażenie na logarytmiczny profil prędkości:
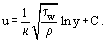
Jeżeli używane są współrzędne bezwymiarowe (lub uniwersalne).

gdzie jest tak zwaną prędkością dynamiczną (lub prędkością tarcia), równanie (20) może być przepisane na tzw. prędkość dynamiczną (lub prędkość tarcia). (20) może być przepisany w następującej postaci:
jest tak zwaną prędkością dynamiczną (lub prędkością tarcia), równanie (20) może być przepisane na tzw. prędkość dynamiczną (lub prędkość tarcia). (20) może być przepisany w następującej postaci:
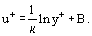
Oprezentacja rozkładu prędkości we współrzędnych uniwersalnych i modele matematyczne dla współczynnika lepkości turbulentnej są omówione bardziej szczegółowo w rozdziale Przepływ turbulentny.
Jedna z aktualnych wersji półempirycznej teorii turbulentnej warstwy granicznej opracowana przez S. S. Kutateladze i A. I. Leontiewa oparta jest na tzw. asymptotycznej teorii turbulentnych warstw brzegowych przy Re → ∞ gdzie grubość laminarnej (lepkiej) podwarstwy δ1 maleje z większą szybkością niż δ w wyniku czego (δ1/δ) → 0.
W tych warunkach rozwija się turbulentna warstwa brzegowa o „znikającej lepkości”. W tej warstwie η → 0, ale nie jest równa zeru i pod tym względem warstwa ta różni się od idealnego przepływu płynu. Pojęcie prawa tarcia względnego, wprowadzone przez S. S. Kutateladze i A. I. Leontiewa (1990), wskazuje
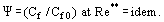
Prawo to definiuje się jako stosunek współczynnika tarcia Cf dla rozpatrywanego warunku do wartości Cf0 dla warunków „standardowych” na płaskiej, nieprzepuszczalnej płycie opływanej przez nieściśliwy, izotermiczny przepływ, przy czym oba współczynniki otrzymuje się dla Re** = Ueδ**/ν. Wykazano, że przy Re → ∞; η → 0; i Cf → 0, względna zmienność współczynnika tarcia pod wpływem takich czynników zakłócających jak gradient ciśnienia, ściśliwość, nieizotermiczność, wtłaczanie (zasysanie) przez porowatą ścianę itp. ma wartość skończoną.
Równania wyprowadzone do obliczania wartości Ψ mają jedną ważną cechę, która uniezależnia Ψ od empirycznych stałych turbulencji. Zgodnie z fundamentalną koncepcją „podejścia” całkowego, całkowe równanie pędu przekształca się w:
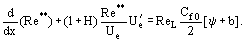
Tutaj, ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) są parametrami przepuszczalności dla przypadku wtłaczania gazu o gęstości ρw przez przepuszczalną ścianę z prędkością vw. W celu wyznaczenia funkcji Re** = Re**
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) są parametrami przepuszczalności dla przypadku wtłaczania gazu o gęstości ρw przez przepuszczalną ścianę z prędkością vw. W celu wyznaczenia funkcji Re** = Re** konieczne jest obliczenie rozkładu
konieczne jest obliczenie rozkładu W tym celu obowiązuje zasada superpozycji czynników zakłócających
W tym celu obowiązuje zasada superpozycji czynników zakłócających

W równ. 24, każdy mnożnik reprezentuje prawo tarcia względnego, uwzględniającego wpływ jednego z czynników, wśród nich ściśliwość ΨM, temperaturę (lub entalpię) głowicy ΨT, wtrysk ΨB, gradient ciśnienia ΨP i inne.
Podstawowe pojęcia warstwy granicznej stwarzają warunki do wyjaśnienia takich zjawisk jak oddzielanie się przepływu od powierzchni pod wpływem bezwładności przepływu, hamowanie przepływu lepkiego przez ściankę i niekorzystny gradient ciśnienia działający w kierunku upstream = 0 lub < 0.
Jeśli gradient ciśnienia jest niekorzystny w miejscu powierzchni pomiędzy sekcjami „1-4” (patrz rys. 3), rozkład prędkości u = u(x,y) w warstwie granicznej zmienia się stopniowo; stając się „mniej pełny”, zmniejszając nachylenie w strumieniach płynu, które są bliżej ściany i posiadają mniejszą ilość energii kinetycznej (patrz kształty profilu prędkości na rys. 3), które przenikają daleko w dół do regionu zwiększonego ciśnienia. W niektórych przekrojach, na przykład w przekroju „4”, cząstki płynu, które znajdują się na linii strumienia „a-a” (linia przerywana na rysunku 3) – po całkowitym wyczerpaniu zapasu energii kinetycznej ulegają wyhamowaniu (ua = 0).
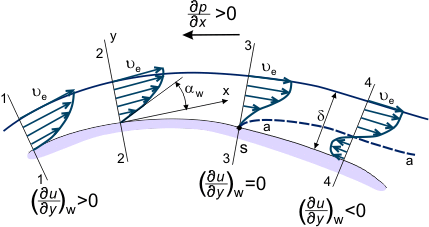
Rysunek 3. Warstwa graniczna w przepływie nad zakrytą powierzchnią.
Ciśnienie statyczne i wartość gradientu ciśnienia nie zmieniają się w zależności od grubości warstwy granicznej. Dlatego cząsteczki płynu znajdujące się bliżej ścianki niż linia „a-a” i posiadające jeszcze mniejszą ilość energii zaczynają się poruszać w przeciwnym kierunku pod wpływem gradientu ciśnienia w przekroju „4-4” (patrz rys. 3). Stąd zależność:

W ten sposób, w niektórych miejscach powierzchni, profil prędkości ulega zmianie. Zmiana ta charakteryzuje się zmianą znaku pochodnej w z dodatniego (odcinek 2, rys. 3) na ujemny (odcinek 4). Oczywiście możliwe jest również zdefiniowanie przekroju, w którym w = 0 (przekrój 3, rysunek 3). Określa się go jako odcinek separacji warstwy granicznej (odpowiednio punkt „S” na powierzchni tego odcinka jest punktem separacji). Charakteryzuje się on powstaniem strefy przepływu wstecznego – przepływ wokół ciała nie jest już gładki, warstwa graniczna staje się znacznie grubsza, a zewnętrzne linie strumienia przepływu odchylają się od powierzchni ciała opływającego. Poniżej punktu separacji rozkład ciśnienia statycznego w całej grubości warstwy nie jest stały, a rozkład ciśnienia statycznego wzdłuż powierzchni nie odpowiada rozkładowi ciśnienia w zewnętrznym, inwazyjnym przepływie.
Po separacji następuje rozwój stref przepływu wstecznego i wirów, w których energia kinetyczna dostarczona z przepływu zewnętrznego przekształca się w ciepło pod wpływem sił tarcia. Separacja przepływu, której towarzyszy rozpraszanie energii w strefach wirów przepływu wstecznego, powoduje takie niepożądane efekty, jak wzrost oporu latających pojazdów czy straty hydrauliczne w kanałach.
Z drugiej strony, przepływy rozdzielone są stosowane w różnych urządzeniach do intensywnego mieszania cieczy (na przykład do poprawy mieszania paliwa i powietrza w komorach spalania silników). Gdy ciecze lepkie przepływają w kanałach o zmiennym przekroju poprzecznym (zmienny gradient ciśnienia), strefa oddzielenia może być lokalna, jeżeli po sekcji dyfuzora następuje sekcja konfuzora, gdzie oddzielony przepływ ponownie przylgnie do powierzchni (patrz rys. 4a). Gdy przepływ oddziela się od krawędzi wleczonej ciała (na przykład od krawędzi wleczonej skrzydła), powstaje tzw. wake, czyli „łączące się” warstwy graniczne (patrz Rysunek 4b).
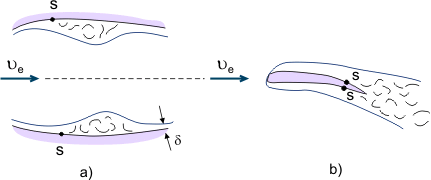
Rysunek 4. Zjawiska separacji warstw granicznych.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. and Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.
.