Uno strato limite è un sottile strato di fluido viscoso vicino alla superficie solida di una parete in contatto con una corrente in movimento in cui (entro il suo spessore δ) la velocità del flusso varia da zero alla parete (dove il flusso “si attacca” alla parete a causa della sua viscosità) fino a Ue al confine, che corrisponde approssimativamente (entro l’1% di errore) alla velocità della corrente libera (vedi Figura 1). In senso stretto, il valore di δ è un valore arbitrario perché la forza di attrito, dipendente dall’interazione molecolare tra il fluido e il corpo solido, diminuisce con la distanza dalla parete e diventa uguale a zero all’infinito.
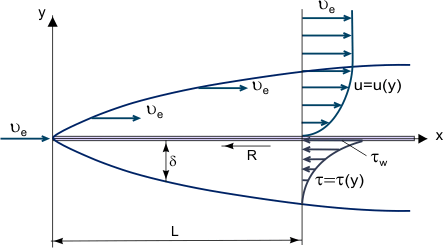
Figura 1. Crescita di uno strato limite su una piastra piana.
Il concetto fondamentale di strato limite fu suggerito da L. Prandtl (1904), esso definisce lo strato limite come uno strato di fluido che si sviluppa in flussi con numeri di Reynolds Re molto alti, cioè con viscosità relativamente bassa rispetto alle forze d’inerzia. Questo si osserva quando i corpi sono esposti a una corrente d’aria ad alta velocità o quando i corpi sono molto grandi e la velocità della corrente d’aria è moderata. In questo caso, in uno strato limite relativamente sottile, l’attrito Shear Stress (forza di taglio viscosa): τ = η (dove η è la viscosità dinamica; u = u(y) – “profilo” della componente di velocità longitudinale dello strato limite, vedi Figura 1) può essere molto grande; in particolare, alla parete dove u = 0 e τw = ηw sebbene la viscosità stessa possa essere piuttosto piccola.
È possibile ignorare le forze di attrito al di fuori dello strato limite (rispetto alle forze di inerzia), e sulla base del concetto di Prandtl, considerare due regioni di flusso: lo strato limite dove gli effetti di attrito sono grandi e il nucleo del flusso quasi Inviscid. Partendo dalla premessa che lo strato limite è uno strato molto sottile (δ << L, dove L è la dimensione lineare caratteristica del corpo su cui avviene il flusso o del canale contenente il flusso, il cui spessore diminuisce al crescere di Re, Figura 1), si può stimare l’ordine di grandezza dello spessore dello strato limite dalla seguente relazione:
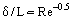
Per esempio, quando un aereo vola a Ue = 400 km/ora, lo spessore dello strato limite al bordo di uscita dell’ala con 1 metro di corda (lunghezza del profilo) è 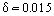 m. Come è stato stabilito sperimentalmente, uno strato limite laminare si sviluppa nella sezione di ingresso del corpo. Gradualmente, sotto l’influenza di alcuni fattori destabilizzanti, lo strato limite diventa instabile e la transizione dello strato limite in un regime di flusso turbolento ha luogo. Speciali indagini sperimentali hanno stabilito l’esistenza di una regione di transizione tra la regione turbolenta e quella laminare. In alcuni casi (per esempio, ad alto livello di turbolenza del flusso esterno), lo strato limite diventa turbolento immediatamente a valle del punto di stagnazione del flusso. In alcune condizioni, come una forte caduta di pressione, nei flussi turbolenti in accelerazione si verifica un fenomeno inverso, cioè la rilaminarizzazione del flusso.
m. Come è stato stabilito sperimentalmente, uno strato limite laminare si sviluppa nella sezione di ingresso del corpo. Gradualmente, sotto l’influenza di alcuni fattori destabilizzanti, lo strato limite diventa instabile e la transizione dello strato limite in un regime di flusso turbolento ha luogo. Speciali indagini sperimentali hanno stabilito l’esistenza di una regione di transizione tra la regione turbolenta e quella laminare. In alcuni casi (per esempio, ad alto livello di turbolenza del flusso esterno), lo strato limite diventa turbolento immediatamente a valle del punto di stagnazione del flusso. In alcune condizioni, come una forte caduta di pressione, nei flussi turbolenti in accelerazione si verifica un fenomeno inverso, cioè la rilaminarizzazione del flusso.
Nonostante la sua relativa sottigliezza, lo strato limite è molto importante per avviare i processi di interazione dinamica tra il flusso e il corpo. Lo strato limite determina la resistenza aerodinamica e la portanza del veicolo volante, o la perdita di energia per il flusso fluido nei canali (in questo caso, uno strato limite idrodinamico perché c’è anche uno strato limite termico che determina l’interazione termodinamica del trasferimento di calore).
Il calcolo dei parametri dello strato limite si basa sulla soluzione delle equazioni ottenute dalle equazioni di Navier-Stokes per il moto dei fluidi viscosi, che sono prima notevolmente semplificate tenendo conto della sottigliezza dello strato limite.
La soluzione suggerita da L. Prandtl è essenzialmente il primo termine dell’espansione in serie dell’equazione di Navier-Stokes, l’espansione in serie viene eseguita per potenze del parametro adimensionale (δ/L). Il parametro più piccolo in questo termine è in potenza zero in modo che l’equazione dello strato limite sia l’approssimazione zero in un’espansione asintotica (a grande Re) dell’equazione dello strato limite (soluzione asintotica).
Una trasformazione dell’equazione di Navier-Stokes nelle equazioni dello strato limite può essere dimostrata derivando l’equazione di Prandtl per lo strato limite laminare in un flusso bidimensionale incomprimibile senza forze del corpo.
In questo caso, il sistema di equazioni di Navier-Stokes sarà:

Dopo aver valutato l’ordine di grandezza di alcuni termini dell’Eq. (2) e ignorando i termini piccoli il sistema di equazioni di Prandtl per lo strato limite laminare diventa:

in cui x, y sono coordinate longitudinali e laterali (Figura 1); v è la componente di velocità lungo l’asse “y”; p, pressione; t, tempo; e n la viscosità cinematica.
Lo strato limite è sottile e la velocità al suo bordo esterno Ue può essere sufficientemente e accuratamente determinata come la velocità di un flusso fluido ideale (inviscido) lungo la parete calcolata fino alla prima approssimazione, senza considerare l’azione inversa dello strato limite sul flusso esterno. Il gradiente di pressione longitudinale = (a p(y) = const) in Eq. (3) può essere rappresentato dall’equazione di Eulero del moto di un fluido ideale. Da quanto sopra, le equazioni di Prandtl nella loro forma finita saranno scritte come:

Questo è un sistema di equazioni differenziali paraboliche non lineari del secondo ordine che sono risolte con condizioni iniziali e al contorno


Il sistema di equazioni (4) è scritto per valori reali delle componenti di velocità u e v. Per generalizzare le equazioni ottenute per il flusso turbolento, si dovrebbe usare la ben nota relazione tra le componenti effettive, medie e pulsanti dei parametri dei flussi turbolenti. Per esempio, per le componenti di velocità ci sono relazioni che collegano le componenti effettive u e v, medie ū e e pulsanti u’ e v’:
e pulsanti u’ e v’:

Dopo alcuni riarrangiamenti, è possibile ottenere un altro sistema di equazioni dal sistema (3), in particolare per il flusso stazionario:
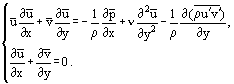
Utilizzando la seguente relazione per lo sforzo di taglio per attrito nello strato limite:
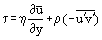
e tenendo conto che nello strato limite laminare u = u’ e è possibile riscrivere le equazioni di Prandtl in una forma valida sia per flussi laminari che turbolenti:
è possibile riscrivere le equazioni di Prandtl in una forma valida sia per flussi laminari che turbolenti:
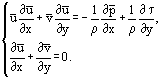
Le soluzioni più semplici sono state ottenute per uno strato limite laminare su una sottile piastra piatta in un flusso bidimensionale e parallelo di fluido incomprimibile (Figura 1). In questo caso, la stima dell’ordine di grandezza dei termini delle equazioni: x ~ L, y ~ δ, δ ~ permette di combinare le variabili x e y in una relazione
permette di combinare le variabili x e y in una relazione

e di ridurre la soluzione dell’Eq. (8) (a dp/dx = 0) per determinare le dipendenze di u e v dal nuovo parametro ξ. D’altra parte, utilizzando le ben note relazioni tra le componenti di velocità u, v e la funzione di flusso ψ

è possibile ottenere una equazione differenziale ordinaria non lineare del terzo ordine, invece del sistema di equazioni differenziali parziali (8)

Qui, f(ξ) è la funzione sconosciuta della variabile ξ: f = ƒ =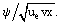
La prima soluzione numerica dell’Eq. (10) è stata ottenuta da Blasius (1908) in condizioni limite corrispondenti alle condizioni fisiche dello strato limite a y = 0: u = 0, v = 0; a y → ∞; u → Ue (strato limite di Blasius).
La figura 2 confronta i risultati della soluzione di Blasius (linea continua) con i dati sperimentali. Usando questi dati, è possibile valutare lo spessore dello strato limite viscoso. A ξ  2.5, (u/Ue
2.5, (u/Ue 0.99) (Figura 2); di conseguenza dalla Eq. (9) si ottiene:
0.99) (Figura 2); di conseguenza dalla Eq. (9) si ottiene:

Figura 2.
Dai calcoli numerici di Blasius del valore della derivata seconda della funzione f(ξ) allo sforzo di taglio per attrito della parete, la relazione in questo caso è:

La forza di attrito R, agente su entrambi i lati della piastra di lunghezza L (Figura 1), è determinata anche dall’Eq. (11):

come nel coefficiente di attrito per le piastre piane:
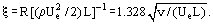
Nonostante il fatto che le equazioni di Prandtl siano molto più semplici delle equazioni di Navier-Stokes, le loro soluzioni sono state ottenute per un numero limitato di problemi. Per molti problemi pratici, non è necessario determinare i profili di velocità nello strato limite, solo lo spessore e lo sforzo di taglio. Questo tipo di informazioni può essere ottenuto risolvendo l’equazione integrale della quantità di moto

La relazione integrale (12) è valida sia per lo strato limite laminare che turbolento.
Funzioni che non erano note a priori ma che caratterizzano la distribuzione dei parametri del fluido attraverso lo spessore δ dello strato sono sotto l’integrale nell’Eq. (12). E l’errore di calcolo dell’integrale è inferiore all’errore nella funzione integranda approssimativamente assunta ρu = ρu(y). Queste condizioni creano le condizioni per sviluppare metodi approssimati di calcolo dei parametri dello strato limite che sono meno dispendiosi in termini di tempo dei metodi esatti di integrazione delle equazioni di Prandtl. Il concetto fondamentale è stato suggerito per la prima volta da T. von Karman, che ha introdotto tale spessore arbitrario dello strato δ*
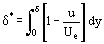
e lo spessore dello spostamento di momento δ**
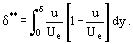
così, possiamo trasformare la Eq. (12) per uno strato limite bidimensionale di fluido incomprimibile in:

Ci sono tre funzioni sconosciute nell’Eq. (15), cioè δ* = δ*(x), δ** = δ**(x) e τw = τw(x).
La soluzione di un’equazione differenziale ordinaria come Eq. (15) di solito richiede l’assunzione (o la rappresentazione) della distribuzione della velocità (profilo di velocità) attraverso lo spessore dello strato limite come funzione di alcuni parametri caratteristici (parametri di forma), e richiede anche l’uso di dati empirici sulla relazione tra il coefficiente di attrito Cf = 2τw/(ρU2e) e lo spessore arbitrario dello strato limite (legge di attrito).
Alcune spiegazioni fisiche definite possono essere date per quanto riguarda i valori di δ* e δ**. La funzione integranda nell’Eq. (13) contiene, dopo il riordinamento, un termine (Ue – u) che caratterizza la diminuzione della velocità. L’integrale in Eq. (14) può quindi essere considerato come una misura della diminuzione della portata attraverso lo strato limite, rispetto al flusso perfetto del fluido alla velocità Ue. D’altra parte, il valore di δ* può essere considerato come la misura della deviazione lungo una normale alla parete (lungo l’asse “y”) della linea di flusso esterno sotto l’influenza delle forze di attrito. Da questa considerazione della struttura integrale dell’Eq. (14), è possibile concludere che δ** caratterizza la diminuzione di quantità di moto nello strato limite sotto l’influenza dell’attrito.
Sono valide le seguenti relazioni:

dove H è il parametro di forma del profilo di velocità dello strato limite. Per esempio, per la distribuzione lineare u = ky,
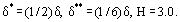
Al momento, le cosiddette teorie semi-empiriche sono ampiamente utilizzate per prevedere i parametri dello strato limite turbolento. In questo caso, si assume che lo stress da attrito totale τ in uno strato limite turbolento sia una somma

Qui, τT è lo stress da attrito aggiuntivo (turbolento o di Reynolds), in particolare, in un flusso incomprimibile vedi Eq. (7).
vedi Eq. (7).
Questa rappresentazione è direttamente collegata al sistema di equazioni del moto nello strato limite (6). Nello strato limite comprimibile, le pulsazioni di densità possono essere considerate come il risultato delle pulsazioni di temperatura

dove β = (1/T) è il coefficiente di espansione volumetrica.
Per determinare τT si usano altre ipotesi semi-empiriche sul trasferimento di quantità di moto turbolento. Per esempio,

dove ηT è il coefficiente dinamico di viscosità turbolenta introdotto da J. Boussinesq nel 1877.
Sulla base del concetto di similarità degli scambi molecolari e turbolenti (teoria della similarità) Prandtl ha introdotto l’ipotesi della lunghezza di mescolamento (die Mischungsweg). La lunghezza di mescolamento 1 è il percorso che un volume fluido finito (“mole”) compie da uno strato di moto medio ad un altro senza cambiare la sua quantità di moto. In accordo con questa condizione, egli derivò un’equazione che si rivelò fondamentale per la teoria dello strato limite:

Per la regione turbolenta dello strato limite del flusso vicino alla parete, L. Prandtl considerava la lunghezza 1 proporzionale a y

dove κ è una costante empirica.
Vicino alla parete, dove ηT << η, l’attrito molecolare viscoso è un fattore determinante. Lo spessore di questa parte dello strato limite δ1, che è noto come sottostrato laminare o viscoso, è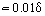 . Al di fuori del sottostrato, il valore di ηT aumenta, raggiungendo diversi ordini di grandezza più grandi di η. Corrispondentemente, in questa zona dello strato limite nota come nucleo turbolento τT > 0 = η. A volte il nucleo turbolento è suddiviso nella zona cuscinetto, dove l’attrito laminare e turbolento sono il valore comparabile, e la zona sviluppata, dove τT >> τ0. Per questa regione, dopo aver integrato l’Eq. (18) e tenuto conto dell’Eq. (19), è possibile ricavare un’espressione per il profilo di velocità logaritmica:
. Al di fuori del sottostrato, il valore di ηT aumenta, raggiungendo diversi ordini di grandezza più grandi di η. Corrispondentemente, in questa zona dello strato limite nota come nucleo turbolento τT > 0 = η. A volte il nucleo turbolento è suddiviso nella zona cuscinetto, dove l’attrito laminare e turbolento sono il valore comparabile, e la zona sviluppata, dove τT >> τ0. Per questa regione, dopo aver integrato l’Eq. (18) e tenuto conto dell’Eq. (19), è possibile ricavare un’espressione per il profilo di velocità logaritmica:
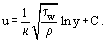
Se si usano coordinate adimensionali (o universali).

dove è la cosiddetta velocità dinamica (o velocità di frizione), l’Eq. (20) può essere riscritta nella forma seguente:
è la cosiddetta velocità dinamica (o velocità di frizione), l’Eq. (20) può essere riscritta nella forma seguente:
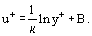
La rappresentazione della distribuzione della velocità in coordinate universali e i modelli matematici per il coefficiente di viscosità turbolenta sono trattati più in dettaglio nella sezione del flusso turbolento.
Una delle versioni attuali della teoria semi-empirica dello strato limite turbolento sviluppata da S. S. Kutateladze e A. I. Leontiev si basa sulla cosiddetta teoria asintotica degli strati limite turbolenti a Re → ∞ dove lo spessore del sottostrato laminare (viscoso) δ1 diminuisce ad una velocità maggiore di δ in conseguenza della quale (δ1/δ) → 0.
In queste condizioni, si sviluppa uno strato limite turbolento con “viscosità vanificante”. In questo strato, η → 0 ma non è uguale a zero e in questo senso, lo strato differisce dal flusso fluido perfetto. Il concetto di legge di attrito relativo, introdotto da S. S. Kutateladze e A. I. Leontiev (1990), indica
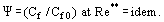
La legge è definita come il rapporto tra il coefficiente di attrito Cf per la condizione in esame e il valore di Cf0 per condizioni “standard” su una piastra piana e impermeabile percorsa da un flusso incomprimibile e isotermo, entrambi i coefficienti essendo ottenuti per Re** = Ueδ**/ν. Si dimostra che a Re → ∞; η → 0; e Cf → 0, la variazione relativa del coefficiente di attrito sotto l’influenza di fattori di disturbo come il gradiente di pressione, la compressibilità, la non isotermicità, l’iniezione (aspirazione) attraverso una parete porosa ecc. ha un valore finito.
Le equazioni derivate per calcolare il valore di Ψ hanno una caratteristica importante che rende Ψ indipendente dalle costanti empiriche di turbolenza. In accordo con il concetto fondamentale dell'”approccio” integrale, l’equazione integrale della quantità di moto è trasformata in:
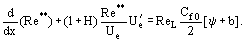
Qui, ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) sono i parametri di permeabilità per il caso di iniezione di un gas a densità ρw attraverso una parete permeabile alla velocità di vw. Per determinare la funzione Re** = Re**
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) sono i parametri di permeabilità per il caso di iniezione di un gas a densità ρw attraverso una parete permeabile alla velocità di vw. Per determinare la funzione Re** = Re** , è necessario calcolare la distribuzione
, è necessario calcolare la distribuzione A questo scopo, si applica il principio di sovrapposizione dei fattori di disturbo
A questo scopo, si applica il principio di sovrapposizione dei fattori di disturbo

In Eq. 24, ogni moltiplicatore rappresenta la legge di attrito relativa, tenendo conto dell’effetto di uno dei fattori, tra cui la compressibilità ΨM, la temperatura (o entalpia) di testa ΨT, l’iniezione ΨB, il gradiente di pressione ΨP e altri.
I concetti fondamentali dello strato limite creano le condizioni per spiegare fenomeni come la separazione del flusso dalla superficie sotto l’influenza dell’inerzia del flusso, la decelerazione del flusso viscoso da parte della parete e il gradiente di pressione avverso che agisce nella direzione a monte = 0 o < 0.
Se il gradiente di pressione è avverso nella posizione superficiale tra le sezioni ‘1-4’ (vedi Figura 3), la distribuzione di velocità u = u(x,y) nello strato limite cambia gradualmente; diventando “meno piena”, diminuendo l’inclinazione nei getti fluidi che sono più vicini alla parete e possedendo meno quantità di energia cinetica (vedi forme del profilo di velocità in Figura 3) che penetrano molto a valle nella regione di aumento della pressione. In alcune sezioni, per esempio la sezione ‘4’, le particelle di fluido che si trovano sulla linea di flusso ‘a-a’ (linea tratteggiata nella Figura 3) – avendo completamente esaurito la loro riserva di energia cinetica diventano decelerate (ua = 0).
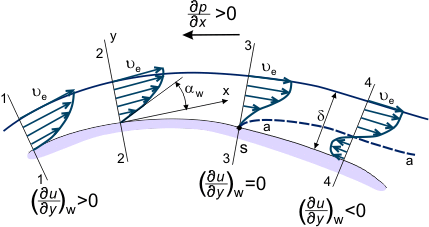
Figura 3. Strato limite nel flusso su una superficie coperta.
La pressione statica e il valore del gradiente di pressione non variano attraverso lo spessore dello strato limite. Pertanto, le particelle di fluido che sono più vicine alla parete rispetto alla linea ‘a-a’ e che possiedono ancora meno energia iniziano a muoversi nella direzione opposta sotto l’influenza del gradiente di pressione nella sezione ‘4-4’ (vedi Figura 3). Così, la relazione:

In questo modo, in alcuni punti della superficie, il profilo di velocità cambia. Questo cambiamento è caratterizzato dall’alterazione del segno della derivata w da positivo (sezione 2, figura 3) a negativo (sezione 4). Naturalmente, è anche possibile definire la sezione in cui w = 0 (sezione 3, figura 3). Questo è indicato come la sezione di separazione dello strato limite (corrispondentemente il punto ‘S’ sulla superficie di questa sezione è il punto di separazione). È caratterizzato dallo sviluppo di una zona di flusso inverso – il flusso intorno al corpo non è più liscio, lo strato limite diventa considerevolmente più spesso e le linee di flusso esterne deviano dalla superficie del corpo volato intorno. A valle del punto di separazione, la distribuzione della pressione statica attraverso lo spessore dello strato non è costante e la distribuzione della pressione statica lungo la superficie non corrisponde alla distribuzione della pressione nel flusso inviscido esterno.
La separazione è seguita dallo sviluppo di zone di flusso inverso e vortici, in cui l’energia cinetica fornita dal flusso esterno si trasforma in calore sotto l’influenza delle forze di attrito. La separazione del flusso, accompagnata dalla dissipazione di energia nelle zone di vortici a flusso inverso, provoca effetti indesiderati come l’aumento della resistenza dei veicoli in volo o le perdite idrauliche nei canali.
D’altra parte, i flussi separati sono utilizzati in diversi dispositivi per la miscelazione intensiva del fluido (per esempio, per migliorare la miscelazione di carburante e aria nelle camere di combustione dei motori). Quando fluidi viscosi scorrono in canali con una sezione trasversale variabile (gradiente di pressione alternato), la zona di separazione può essere locale se la sezione diffusore è seguita dalla sezione confusore, dove il flusso separato si riattacca nuovamente alla superficie (vedi Figura 4a). Quando il flusso si separa dal bordo di uscita del corpo (per esempio, dal bordo di uscita dell’ala), la cosiddetta scia è formata da strati limite “di collegamento” (vedi Figura 4b).
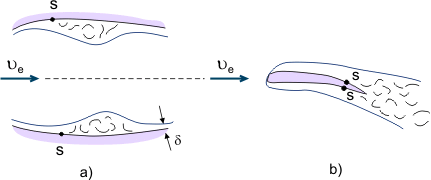
Figura 4. Fenomeni di separazione degli strati limite.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. e Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.