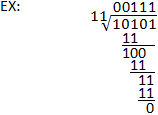Utilizza le seguenti calcolatrici per eseguire l’addizione, la sottrazione, la moltiplicazione o la divisione di due valori binari, oltre a convertire valori binari in valori decimali e viceversa.

Calcolo binario – Aggiungere, sottrarre, moltiplicare, o dividi
Convertire valore binario in valore decimale
Convertire valore decimale in valore binario
Calcolatrice esadecimale correlata | Calcolatrice subnet IP
Il sistema binario è un sistema numerico che funziona in modo praticamente identico al sistema di numeri decimali con cui le persone hanno probabilmente più familiarità. Mentre il sistema decimale usa il numero 10 come base, il sistema binario usa 2. Inoltre, anche se il sistema decimale usa le cifre da 0 a 9, il sistema binario usa solo 0 e 1, e ogni cifra è indicata come un bit. A parte queste differenze, operazioni come l’addizione, la sottrazione, la moltiplicazione e la divisione sono tutte calcolate seguendo le stesse regole del sistema decimale.
Quasi tutta la tecnologia moderna e i computer usano il sistema binario a causa della sua facilità di implementazione nei circuiti digitali usando porte logiche. È molto più semplice progettare hardware che ha solo bisogno di rilevare due stati, on e off (o vero/falso, presente/assente, ecc.). Usare un sistema decimale richiederebbe un hardware che può rilevare 10 stati per le cifre da 0 a 9, ed è più complicato.
Di seguito ci sono alcune tipiche conversioni tra valori binari e decimali:
Conversione binaria/decimale
| Decimale | Binario |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Mentre lavorare con il binario può sembrare inizialmente confuso, capire che ogni valore di posto binario rappresenta 2n, proprio come ogni posto decimale rappresenta 10n, dovrebbe aiutare a chiarire. Prendiamo il numero 8 per esempio. Nel sistema numerico decimale, l’8 è posizionato nel primo posto decimale a sinistra della virgola, che rappresenta il posto 100. Essenzialmente questo significa:
8 × 100 = 8 × 1 = 8
Utilizzando il numero 18 per confronto:
(1 × 101) + (8 × 100) = 10 + 8 = 18
In binario, 8 è rappresentato come 1000. Leggendo da destra a sinistra, il primo 0 rappresenta 20, il secondo 21, il terzo 22 e il quarto 23; proprio come il sistema decimale, ma con una base di 2 invece di 10. Poiché 23 = 8, si inserisce un 1 nella sua posizione, ottenendo 1000. Usando 18, o 10010 come esempio:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Il processo passo passo per convertire dal sistema decimale a quello binario è:
- Trova la più grande potenza di 2 che si trova all’interno del numero dato
- Sottrai quel valore dal numero dato
- Trova la più grande potenza di 2 all’interno del resto trovato nel passo 2
- Ripeti finché non c’è più resto
- Inserisci un 1 per ogni valore di posto binario che è stato trovato, e uno 0 per il resto
Utilizzando ancora l’obiettivo di 18 come esempio, ecco un altro modo di visualizzare questo:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Istanze entro 18 | 1 | 0 | 0 | 1 | 0 |
| Target: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
Convertire dal sistema binario al decimale è più semplice. Determinare tutti i valori di luogo in cui si verifica 1, e trovare la somma dei valori.
ES: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Dunque: 16 + 4 + 2 + 1 = 23.
Addizione binaria
L’addizione binaria segue le stesse regole dell’addizione nel sistema decimale tranne che, invece di riportare un 1 quando i valori aggiunti sono uguali a 10, il riporto avviene quando il risultato dell’addizione è uguale a 2. Fate riferimento all’esempio qui sotto per un chiarimento.
Nota che nel sistema binario:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, riportare l’1, cioè 10
EX:
| 10 | 11 | 11 | 10 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
L’unica vera differenza tra l’addizione binaria e decimale è che il valore 2 nel sistema binario è equivalente a 10 nel sistema decimale. Si noti che gli 1 in apice rappresentano le cifre che vengono riportate. Un errore comune a cui fare attenzione quando si esegue l’addizione binaria è il caso in cui 1 + 1 = 0 ha anche un 1 riportato dalla colonna precedente alla sua destra. Il valore in basso dovrebbe quindi essere 1 dall’1 riportato piuttosto che 0. Questo può essere osservato nella terza colonna da destra nell’esempio sopra.
Sottrazione binaria
Similmente all’addizione binaria, c’è poca differenza tra la sottrazione binaria e decimale tranne quelle che derivano dall’uso delle sole cifre 0 e 1. Il prestito si verifica in ogni caso in cui il numero che viene sottratto è maggiore del numero da cui viene sottratto. Nella sottrazione binaria, l’unico caso in cui il prestito è necessario è quando si sottrae 1 da 0. Quando questo accade, lo 0 nella colonna che prende in prestito diventa essenzialmente “2” (cambiando lo 0-1 in 2-1 = 1) mentre riduce l’1 nella colonna da cui viene preso in prestito di 1. Se la colonna seguente è anche 0, il prestito dovrà avvenire da ogni colonna successiva fino a quando una colonna con un valore di 1 può essere ridotta a 0. Fare riferimento all’esempio seguente per chiarimenti.
Nota che nel sistema binario:
- 0 – 0 = 0
0 – 1 = 1, prendendo in prestito 1, con conseguente -1 riportato
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | |||
| – | 0 | 1 | 1 | 0 | 1 | ||
| = | 0 | 1 | 0 | 1 | 1 | 0 | |
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Nota che gli apici visualizzati sono i cambiamenti che avvengono ad ogni bit quando si prende in prestito. La colonna che prende in prestito essenzialmente ottiene 2 dal prestito, e la colonna da cui viene preso in prestito viene ridotta di 1.
Moltiplicazione binaria
La moltiplicazione binaria è probabilmente più semplice della sua controparte decimale. Poiché gli unici valori utilizzati sono 0 e 1, i risultati che devono essere aggiunti sono o lo stesso del primo termine, o 0. Si noti che in ogni riga successiva, i segnaposto 0 devono essere aggiunti, e il valore spostato a sinistra, proprio come nella moltiplicazione decimale. La complessità nella moltiplicazione binaria deriva dalla noiosa addizione binaria che dipende da quanti bit ci sono in ogni termine. Fate riferimento all’esempio qui sotto per un chiarimento.
Nota che nel sistema binario:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Come si può vedere nell’esempio precedente, il processo di moltiplicazione binaria è lo stesso della moltiplicazione decimale. Si noti che il segnaposto 0 è scritto nella seconda riga. Di solito il segnaposto 0 non è visivamente presente nella moltiplicazione decimale. Mentre lo stesso può essere fatto in questo esempio (con il segnaposto 0 assunto piuttosto che esplicito), è incluso in questo esempio perché lo 0 è rilevante per qualsiasi calcolatrice di addizione/sottrazione binaria, come quella fornita in questa pagina. Senza che lo 0 sia mostrato, sarebbe possibile fare l’errore di escludere lo 0 quando si sommano i valori binari mostrati sopra. Nota di nuovo che nel sistema binario, qualsiasi 0 a destra di un 1 è rilevante, mentre qualsiasi 0 a sinistra dell’ultimo 1 nel valore non lo è.
EX:
- 1 0 1 0 1 1 0 0
= 0 0 1 0 1 0 1 0 0
≠ 1 0 1 0 1 0 0 0 0 0
Divisione binaria
Il processo della divisione binaria è simile alla divisione lunga nel sistema decimale. Il dividendo è ancora diviso per il divisore nello stesso modo, con l’unica differenza significativa che l’uso della sottrazione binaria piuttosto che decimale. Si noti che una buona comprensione della sottrazione binaria è importante per condurre la divisione binaria. Fate riferimento all’esempio qui sotto, così come alla sezione sulla sottrazione binaria per chiarimenti.