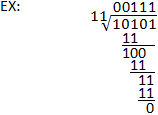Użyj następujących kalkulatorów do wykonywania dodawania, odejmowania, mnożenia lub dzielenia dwóch wartości binarnych, a także do konwersji wartości binarnych na dziesiętne i odwrotnie.

Obliczanie binarne – dodawanie, odejmowanie, mnożenie, lub dzielenie
Konwersja wartości binarnej na dziesiętną
Konwersja wartości dziesiętnej na binarną
Powiązany kalkulator heksadecymalny | Kalkulator podsieci IP
System binarny jest systemem liczbowym, który działa praktycznie tak samo jak dziesiętny system liczbowy, z którym ludzie są prawdopodobnie bardziej zaznajomieni. Podczas gdy dziesiętny system liczbowy wykorzystuje liczbę 10 jako podstawę, system binarny używa 2. Ponadto, chociaż system dziesiętny wykorzystuje cyfry od 0 do 9, system binarny wykorzystuje tylko 0 i 1, a każda cyfra jest określana jako bit. Oprócz tych różnic, operacje takie jak dodawanie, odejmowanie, mnożenie i dzielenie są obliczane zgodnie z tymi samymi zasadami, co w systemie dziesiętnym.
Prawie wszystkie nowoczesne technologie i komputery używają systemu binarnego ze względu na łatwość wdrożenia w obwodach cyfrowych przy użyciu bramek logicznych. Jest to znacznie prostsze do projektowania sprzętu, który musi tylko wykryć dwa stany, włączony i wyłączony (lub prawda/fałsz, obecny/nieobecny, itp.). Użycie systemu dziesiętnego wymagałoby sprzętu, który może wykryć 10 stanów dla cyfr od 0 do 9, i jest bardziej skomplikowane.
Poniżej przedstawiono kilka typowych konwersji między wartościami binarnymi i dziesiętnymi:
Konwersja binarna/dziesiętna
| Decimal | Binary |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Choć praca z binarnymi może początkowo wydawać się myląca, zrozumienie, że każde miejsce binarne reprezentuje 2n, tak jak każde miejsce dziesiętne reprezentuje 10n, powinno pomóc w wyjaśnieniu. Weźmy na przykład liczbę 8. W dziesiętnym systemie liczbowym, 8 jest umieszczony w pierwszym miejscu dziesiętnym w lewo od kropki dziesiętnej, oznaczając 100 miejsce. Zasadniczo oznacza to:
8 × 100 = 8 × 1 = 8
Używając liczby 18 dla porównania:
(1 × 101) + (8 × 100) = 10 + 8 = 18
W systemie binarnym, 8 jest reprezentowane jako 1000. Czytając od prawej do lewej, pierwsze 0 reprezentuje 20, drugie 21, trzecie 22, a czwarte 23; tak jak w systemie dziesiętnym, z wyjątkiem podstawy 2, a nie 10. Ponieważ 23 = 8, na jego miejsce wpisujemy 1, co daje 1000. Używając 18, czyli 10010 jako przykładu:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Proces konwersji z systemu dziesiętnego na binarny jest następujący:
- Znajdź największą potęgę 2, która leży w danej liczbie
- Odejmij tę wartość od danej liczby
- Znajdź największą potęgę 2 w reszcie znalezionej w kroku 2
- Powtarzaj, aż nie będzie reszty
- Wprowadź 1 dla każdej znalezionej wartości miejsca binarnego, i 0 dla reszty
Używając celu 18 ponownie jako przykład, poniżej jest inny sposób, aby to zwizualizować:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Instancje w obrębie 18 | 1 | 0 | 0 | 1 | 0 |
| Target: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
Konwersja z systemu binarnego na dziesiętny jest prostsza. Wyznacz wszystkie wartości miejsc, w których występuje 1 i znajdź sumę tych wartości.
EX: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | |
| 16 | 0 | 4 | 2 | 1 |
Stąd: 16 + 4 + 2 + 1 = 23.
Dodawanie binarne
Dodawanie binarne przebiega według tych samych reguł, co dodawanie w systemie dziesiętnym, z tą różnicą, że zamiast przenoszenia 1 na drugą stronę, gdy dodawane wartości są równe 10, przenoszenie następuje, gdy wynik dodawania jest równy 2. Odnieś się do poniższego przykładu dla wyjaśnienia.
Zauważ, że w systemie binarnym:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, przeniesienie 1, tj. 10
EX:
| 10 | 11 | 11 | 10 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
Jedyną prawdziwą różnicą między dodawaniem binarnym i dziesiętnym jest to, że wartość 2 w systemie binarnym jest odpowiednikiem 10 w systemie dziesiętnym. Zauważ, że cyfry 1 w indeksie górnym reprezentują cyfry, które są przenoszone. Częstym błędem, na który należy uważać podczas wykonywania dodawania binarnego, jest przypadek, w którym 1 + 1 = 0 ma również 1 przeniesioną z poprzedniej kolumny po prawej stronie. Wartość na dole powinna być wtedy 1 z przeniesionej 1, a nie 0. Można to zaobserwować w trzeciej kolumnie od prawej w powyższym przykładzie.
Odejmowanie binarne
Podobnie jak w przypadku dodawania binarnego, istnieje niewiele różnic pomiędzy odejmowaniem binarnym i dziesiętnym, z wyjątkiem tych, które wynikają z używania tylko cyfr 0 i 1. Pożyczanie występuje w każdym przypadku, gdy liczba, która jest odejmowana jest większa niż liczba, od której jest odejmowana. W odejmowaniu binarnym, jedynym przypadkiem, w którym pożyczanie jest konieczne jest, gdy 1 jest odejmowana od 0. Kiedy to nastąpi, 0 w kolumnie pożyczania zasadniczo staje się „2” (zamieniając 0-1 na 2-1 = 1), jednocześnie zmniejszając 1 w kolumnie pożyczanej o 1. Jeśli następna kolumna jest również 0, pożyczanie będzie musiało nastąpić z każdej następnej kolumny, aż kolumna o wartości 1 może być zmniejszona do 0. Odnieś się do poniższego przykładu dla wyjaśnienia.
Zauważ, że w systemie binarnym:
- 0 – 0 = 0
0 – 1 = 1, pożyczamy 1, co skutkuje -1 przeniesionym nad
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | ||
| – | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 1 | 0 | |
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Zauważ, że wyświetlane indeksy górne to zmiany, które zachodzą w każdym bicie podczas zapożyczania. Kolumna pożyczająca zasadniczo uzyskuje 2 z pożyczania, a kolumna, która jest pożyczana od jest zmniejszona o 1.
Mnożenie binarne
Mnożenie binarne jest prawdopodobnie prostsze niż jego odpowiednik dziesiętny. Ponieważ jedynymi używanymi wartościami są 0 i 1, wyniki, które muszą być dodane są albo takie same jak pierwszy warunek, albo 0. Zauważ, że w każdym kolejnym rzędzie, placeholder 0’s muszą być dodane, a wartość przesunięta w lewo, tak jak w mnożeniu dziesiętnym. Złożoność w mnożeniu binarnym wynika z żmudnego dodawania binarnego zależnego od tego, ile bitów jest w każdym z członów. Odnieś się do poniższego przykładu dla wyjaśnienia.
Zauważ, że w systemie binarnym:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Jak widać na powyższym przykładzie, proces mnożenia binarnego jest taki sam jak w przypadku mnożenia dziesiętnego. Zauważ, że 0 placeholder jest napisane w drugiej linii. Zazwyczaj znak 0 nie jest wizualnie obecny w mnożeniu dziesiętnym. Chociaż to samo można zrobić w tym przykładzie (z miejscem 0, które jest zakładane, a nie jawne), jest to zawarte w tym przykładzie, ponieważ 0 jest istotne dla każdego kalkulatora binarnego dodawania / odejmowania, jak ten na tej stronie. Bez 0 jest pokazany, byłoby możliwe, aby popełnić błąd wykluczenia 0 podczas dodawania wartości binarnych wyświetlanych powyżej. Zauważ ponownie, że w systemie binarnym, każde 0 na prawo od 1 jest istotne, podczas gdy każde 0 na lewo od ostatniej 1 w wartości nie jest.
EX:
- 1 0 1 0 1 1 0 0 0
= 0 0 1 0 1 0 1 1 0 0
≠ 1 0 1 0 1 0 0 0
Działanie binarne
Proces dzielenia binarnego jest podobny do długiego dzielenia w systemie dziesiętnym. Dywidenda jest nadal dzielona przez dzielnik w ten sam sposób, z jedyną istotną różnicą jest użycie odejmowania binarnego zamiast dziesiętnego. Zauważ, że dobre zrozumienie odejmowania binarnego jest ważne dla przeprowadzania dzielenia binarnego. Wyjaśnienia można znaleźć w poniższym przykładzie oraz w rozdziale poświęconym odejmowaniu binarnemu.