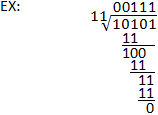Následující kalkulačky slouží k provádění sčítání, odčítání, násobení nebo dělení dvou binárních hodnot a k převodu binárních hodnot na desítkové a naopak.

Binární výpočet – sčítání, odčítání, násobení, nebo dělit
Převod binární hodnoty na desítkovou hodnotu
Převod desítkové hodnoty na binární hodnotu
Související hexadecimální kalkulačka | Kalkulačka IP podsítě
Dvojková soustava je číselná soustava, která funguje prakticky stejně jako desítková číselná soustava, kterou lidé pravděpodobně znají lépe. Zatímco desítková číselná soustava používá jako základ číslo 10, dvojková soustava používá číslo 2. Dále, ačkoli desítková soustava používá číslice 0 až 9, dvojková soustava používá pouze 0 a 1 a každá číslice se označuje jako bit. Kromě těchto rozdílů se operace jako sčítání, odčítání, násobení a dělení počítají podle stejných pravidel jako v desítkové soustavě.
Téměř všechny moderní technologie a počítače používají dvojkovou soustavu díky její snadné implementaci v digitálních obvodech pomocí logických hradel. Je mnohem jednodušší navrhnout hardware, který potřebuje detekovat pouze dva stavy, zapnuto a vypnuto (nebo pravda/nepravda, přítomno/nepřítomno atd.). Použití desítkové soustavy by vyžadovalo hardware, který dokáže detekovat 10 stavů pro číslice 0 až 9, a to je složitější.
Níže jsou uvedeny některé typické převody mezi binárními a desítkovými hodnotami:
Převod dvojkové/desítkové soustavy
| Desítková soustava | Dvojková soustava |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 7 | 111 |
| 8 | 1000 |
| 10 | 1010 |
| 16 | 10000 |
| 20 | 10100 |
Práce s dvojkovou soustavou se může zpočátku zdát matoucí, pochopení, že každé místo ve dvojkové soustavě představuje 2n, stejně jako každé místo v desítkové soustavě představuje 10n, by mělo přispět k objasnění. Vezměme si například číslo 8. V desítkové číselné soustavě je číslo 8 umístěno na prvním desítkovém místě vlevo od desítkové tečky, což znamená 100 místo. V podstatě to znamená:
8 × 100 = 8 × 1 = 8
Použijeme-li pro srovnání číslo 18:
(1 × 101) + (8 × 100) = 10 + 8 = 18
V binární soustavě je 8 reprezentováno jako 1000. Při čtení zprava doleva představuje první 0 číslo 20, druhá 21, třetí 22 a čtvrtá 23; stejně jako v desítkové soustavě, jen se základem 2 místo 10. Protože 23 = 8, je na jeho pozici zapsána jednička, což dává výsledek 1000. Na příkladu 18 neboli 10010:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Postup převodu z desítkové do dvojkové soustavy krok za krokem je následující:
- Najděte největší mocninu 2, která leží v daném čísle
- Odčtěte tuto hodnotu od daného čísla
- Najděte největší mocninu 2 ve zbytku zjištěném v kroku 2
- Pak opakujte, dokud nezbude žádný zbytek
- Zapište 1 pro každou nalezenou dvojkovou hodnotu místa, a 0 pro zbytek
Použijeme-li jako příklad opět cíl 18, níže je uveden další způsob vizualizace:
| 2n | 24 | 23 | 22 | 21 | 20 |
| Instances within 18 | 1 | 0 | 0 | 1 | 0 |
| Target: 18 | 18 – 16 = 2 | → | 2 – 2 = 0 | ||
Převod z dvojkové soustavy na desítkovou je jednodušší. Určete všechny hodnoty míst, kde se vyskytuje 1, a zjistěte součet těchto hodnot.
NAPŘ: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 | 1 |
| 16 | 0 | 4 | 2 | 1 |
Tedy:
Dvojkové sčítání
Dvojkové sčítání se řídí stejnými pravidly jako sčítání v desítkové soustavě s tím rozdílem, že namísto přenášení jedničky v případě, že se sčítané hodnoty rovnají 10, dochází k přenášení v případě, že se výsledek sčítání rovná 2. Objasnění najdete v následujícím příkladu.
Všimněte si, že ve dvojkové soustavě:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, přeneseme 1, tj. 10
EX:
| 10 | 11 | 11 | 10 | 1 | ||
| + | 1 | 0 | 1 | 1 | 1 | |
| = | 1 | 0 | 0 | 1 | 0 | 0 |
Jediný skutečný rozdíl mezi dvojkovou a desítkovou soustavou sčítání je ten, že hodnota 2 ve dvojkové soustavě je ekvivalentní hodnotě 10 v desítkové soustavě. Všimněte si, že číslice s horním indexem 1 představují číslice, které se přenášejí. Častou chybou, na kterou je třeba dávat pozor při provádění binárního sčítání, je případ, kdy 1 + 1 = 0 má vpravo od sebe také přenesenou jedničku z předchozího sloupce. Hodnota dole by pak měla být 1 z přenesené 1, nikoliv 0. To lze pozorovat ve třetím sloupci zprava ve výše uvedeném příkladu.
Dvojkové odčítání
Podobně jako u dvojkového sčítání je mezi dvojkovým a desítkovým odčítáním jen málo rozdílů kromě těch, které vyplývají z použití pouze číslic 0 a 1. K vypůjčování dochází v každém případě, kdy je odčítané číslo větší než číslo, od kterého se odčítá. Při binárním odčítání je výpůjčka nutná pouze v případě, kdy se od 0 odečítá 1. Když k tomu dojde, z 0 ve sloupci, který se půjčuje, se v podstatě stane „2“ (změna 0-1 na 2-1 = 1) a zároveň se 1 ve sloupci, od kterého se půjčuje, zmenší o 1. Pokud je následující sloupec také 0, bude muset dojít k výpůjčce z každého následujícího sloupce, dokud se sloupec s hodnotou 1 nezmenší na 0. Pro objasnění viz příklad níže:
Všimněte si, že ve dvojkové soustavě:
- 0 – 0 = 0
0 – 1 = 1, půjčíme si 1, což vede k přenesení -1
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | ||
| – | 0 | 1 | 1 | 0 | 1 | |
| = | 0 | 1 | 0 | 1 | 0 | |
EX2:
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Všimněte si, že zobrazené horní indexy jsou změny, ke kterým dochází u jednotlivých bitů při půjčování. Vypůjčovaný sloupec v podstatě získá vypůjčením 2 a sloupec, ze kterého se půjčuje, se zmenší o 1.
Dvojkové násobení
Dvojkové násobení je pravděpodobně jednodušší než jeho desítkový protějšek. Protože se používají pouze hodnoty 0 a 1, výsledky, které je třeba sečíst, jsou buď stejné jako první člen, nebo 0. Všimněte si, že v každém dalším řádku je třeba přičíst zástupné 0 a hodnotu posunout doleva, stejně jako při desetinném násobení. Složitost při binárním násobení vzniká zdlouhavým binárním sčítáním závislým na tom, kolik bitů je v každém členu. Objasnění najdete v následujícím příkladu:
Všimněte si, že ve dvojkové soustavě:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
NAPŘ:
| 1 | 0 | 1 | 1 | 1 | |||
| × | 1 | 1 | |||||
| 1 | 0 | 1 | 1 | 1 | |||
| + | 1 | 0 | 1 | 1 | 1 | 0 | |
| = | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
Jak je patrné z výše uvedeného příkladu, postup binárního násobení je stejný jako při násobení v desítkové soustavě. Všimněte si, že ve druhém řádku je zapsána zástupná číslice 0. Při desítkovém násobení se obvykle zástupný znak 0 vizuálně nevyskytuje. Ačkoli totéž lze provést i v tomto příkladu (s tím, že zástupný znak 0 je spíše předpokládaný než explicitní), je v tomto příkladu uveden proto, že 0 je důležitá pro každou kalkulačku binárního sčítání/odečítání, jako je ta, která je uvedena na této stránce. Bez zobrazení 0 by bylo možné při sčítání výše zobrazených binárních hodnot udělat chybu a 0 vyloučit. Znovu si všimněte, že v binární soustavě je každá 0 napravo od jedničky relevantní, zatímco každá 0 nalevo od poslední jedničky v hodnotě relevantní není.
EX:
- 1 0 1 0 1 1 0 0
= 0 0 1 0 1 0 1 1 0 0
≠ 1 0 1 0 1 1 0 0 0
Binární dělení
Postup binárního dělení je podobný dlouhému dělení v desítkové soustavě. Dividenda se stále dělí dělitelem stejným způsobem, jediným podstatným rozdílem je použití binárního, nikoliv desítkového odčítání. Všimněte si, že pro provádění binárního dělení je důležitá dobrá znalost binárního odčítání. Objasnění najdete v následujícím příkladu a také v kapitole o binárním odčítání.