Afskrevet analyse bruges til algoritmer, der har dyre operationer, der kun sker sjældent.

Afskrevet kompleksitetsanalyse bruges oftest med datastrukturer, der har en tilstand, der består mellem operationer.Den grundlæggende idé er, at en dyr operation kan ændre tilstanden, så det værste tilfælde ikke kan forekomme igen i lang tid, hvorved omkostningerne afskrives.
Lad T1, T2, …, Tk være kompleksiteten af en sekvens af operationer på en datastruktur. Den afskrevne kompleksitet af en enkelt operation i denne sekvens er(T1 + T2 + …+ Tk) / k.
Eksempel: et dynamisk array
I et dynamisk array gemmes elementerne i starten af et underliggende fast array, og de resterende positioner er ubrugte.
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Her er en visning af hukommelsen, når man tilføjer elementerne 2, 7, 1, 3, 8, 4til et oprindeligt tomt array med kapacitet 2.
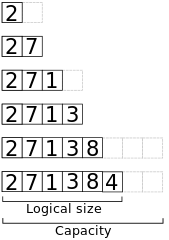
Worst-case-tid
Den værst tænkelige tidskompleksitet for tilføjelse af et elementtil et array af længde n ved hjælp af denne algoritme er Θ(n).Hvis arrayet er fuldt, allokerer algoritmen et nyt array af længde 2n,og kopierer derefter elementerne fra det gamle array til det nye.
Dette resultat er alt for pessimistisk.De følgende n append-operationer vil være meget billigere – hver af dem vil køre på konstant tid, da det nyallokerede array har plads til alle de nye elementer.
Amortiseret tid
En analyse af den amortiserede tid giver en meget bedre forståelse af algoritmen.
Og tænk på en sekvens af n append-operationer,hvor vi starter med et array af længde 1. En omhyggelig analyse viser, at den samlede tid for disse operationer kun er Θ(n).
- Der vil være i alt n tildelingsoperationer og inkrementeringsoperationer med konstant tid.
- Ændringen af størrelsen vil kun ske ved operation 1, 2, 4, …, 2k, hvilket giver i alt 1 + 2 + 4 + …+ 2k = 2-2k – 1 elementkopieringsoperationer med konstant tid. Da 2k ≤ n, er dette højst 2n – 1.
Dermed er den amortiserede tidskompleksitet for en enkelt append-operation Θ(1).
Mere om algoritmeanalyse

Tidskompleksitet: Tæl dine skridt

Big O notation