Et grænselag er et tyndt lag af viskos væske tæt på den faste overflade af en væg i kontakt med en bevægelig strøm, hvor (inden for dets tykkelse δ) strømningshastigheden varierer fra nul ved væggen (hvor strømmen “klæber” til væggen på grund af dens viskositet) op til Ue ved grænsen, hvilket omtrent (med en fejl på 1 %) svarer til den frie strømningshastighed (se figur 1). Strengt taget er værdien δ en vilkårlig værdi, fordi friktionskraften, der afhænger af den molekylære vekselvirkning mellem væsken og det faste legeme, aftager med afstanden fra væggen og bliver lig nul ved uendelighed.
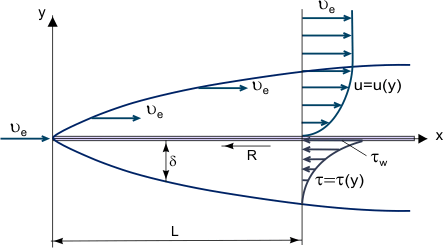
Figur 1. Vækst af et grænselag på en flad plade.
Det grundlæggende begreb om grænselaget blev foreslået af L. Prandtl (1904), det definerer grænselaget som et lag af væske, der udvikler sig i strømninger med meget høje Reynoldstal Re, dvs. med relativt lav viskositet sammenlignet med inerti kræfter. Dette observeres, når legemer udsættes for en luftstrøm med høj hastighed, eller når legemer er meget store, og luftstrømmen har en moderat hastighed. I dette tilfælde, i et relativt tyndt grænselag, kan friktionsshear stress (viskose forskydningskraft): τ = η (hvor η er den dynamiske viskositet; u = u(y) – “profil” af grænselagets langsgående hastighedskomponent, se figur 1) være meget stor; især ved væggen, hvor u = 0 og τw = ηw, selv om selve viskositeten kan være ret lille.
Det er muligt at se bort fra friktionskræfterne uden for grænselaget (i forhold til inertiakræfterne) og på grundlag af Prandtls koncept at betragte to strømningsområder: grænselaget, hvor friktionseffekterne er store, og den næsten inviskide strømningskerne. Under forudsætning af, at grænselaget er et meget tyndt lag (δ << L, hvor L er den karakteristiske lineære dimension af det legeme, hvorover strømningen finder sted, eller den kanal, hvori strømningen foregår, og hvor tykkelsen aftager med væksten af Re, figur 1), kan man anslå størrelsesordenen af grænselagets tykkelse ud fra følgende forhold:
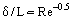
Til eksempel: Når et fly fly flyver med Ue = 400 km/t, er grænselagstykkelsen ved vingens bagkant med 1 meters kordel (profillængde)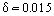 
m. Som det blev eksperimentelt fastslået, udvikles der et laminært grænselag ved indløbsdelen af kroppen. Under indflydelse af nogle destabiliserende faktorer bliver grænselaget gradvist ustabilt, og der sker en overgang fra grænselaget til et turbulent strømningsregime. Særlige eksperimentelle undersøgelser har vist, at der findes et overgangsområde mellem det turbulente og det laminære område. I nogle tilfælde (f.eks. ved et højt turbulensniveau i den eksterne strømning) bliver grænselaget turbulent umiddelbart nedstrøms for strømningens stagnationspunkt. Under visse forhold, som f.eks. et kraftigt trykfald, sker der et omvendt fænomen i accelererende turbulente strømninger, nemlig en relaminarisering af strømningen.
Trods sin relative tyndhed er grænselaget meget vigtigt for at igangsætte processer med dynamisk interaktion mellem strømningen og kroppen. Grænselaget bestemmer det flyvende køretøjs aerodynamiske modstand og løft eller energitabet for væskestrømning i kanaler (i dette tilfælde et hydrodynamisk grænselag, fordi der også findes et termisk grænselag, som bestemmer den termodynamiske interaktion ved varmeoverførsel).
Beregningen af grænselagsparametrene er baseret på løsningen af ligninger, der fås ud fra Navier-Stokes-ligningerne for viskose væskers bevægelse, som først forenkles betydeligt under hensyntagen til grænselagets tyndhed.
Den af L. Prandtl foreslåede løsning er i det væsentlige den første term i potensrækkerudvidelsen af Navier-Stokes-ligningen, idet rækkeudvidelsen udføres for potenser af den dimensionsløse parameter (δ/L). Den mindre parameter i dette term er i null potens, således at grænselagsligningen er nul-approximationen i en asymptotisk ekspansion (ved stort Re) af grænselagsligningen (asymptotisk løsning).
En transformation af Navier-Stokes-ligningen til grænselagsligningerne kan demonstreres ved at udlede Prandtl-ligningen for laminært grænselag i en todimensionel inkompressibel strømning uden kropskræfter.
I dette tilfælde vil systemet af Navier-Stokes-ligninger være:
Efter vurdering af størrelsesordenen af nogle termer i Eq. (2) og ved at se bort fra små termer bliver systemet af Prandtl-ligninger for laminært grænselag:
i hvilke x, y er længde- og sidekoordinater (figur 1); v er hastighedskomponenten langs “y”-aksen; p, tryk; t, tid; og n den kinematiske viskositet.
Grænselaget er tyndt, og hastigheden ved dets ydre kant Ue kan bestemmes tilstrækkeligt og nøjagtigt som hastigheden af en ideel (inviskid) væskestrømning langs væggen beregnet op til første tilnærmelse, uden at der tages hensyn til grænselagets omvendte virkning på den ydre strømning. Den langsgående trykgradient = (ved p(y) = const) i ligning (3) kan beskrives ud fra Eulers bevægelsesligning for en ideel væske. Ud fra ovenstående kan Prandtl-ligningerne i deres finitte form skrives som:
Dette er et system af parabolske, ikke-lineære partielle differentialligninger af anden orden, som løses med begyndelses- og randbetingelser
Systemet af ligninger (4) er skrevet for faktiske værdier af hastighedskomponenterne u og v. For at generalisere de ligninger, der er opnået for turbulente strømninger, bør den velkendte relation mellem faktiske, gennemsnitlige og pulserende komponenter af parametre for turbulente strømninger anvendes. For hastighedskomponenterne er der f.eks. relationer, der forbinder de faktiske u- og v-komponenter, de gennemsnitlige ū- og 
og de pulserende u’- og v’-komponenter:
Efter nogle omarrangeringer er det muligt at få et andet ligningssystem ud fra system (3), især for stationær strømning:
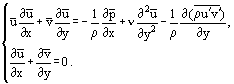
Ved anvendelse af følgende relation for gnidningsskubspænding i grænselaget:
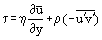
og under hensyntagen til, at i det laminære grænselag er u = u’ og
det er muligt at omskrive Prandtl-ligningerne i en form, der gælder for både laminære og turbulente strømninger:
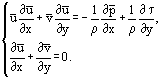
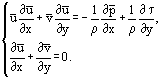
De enkleste løsninger er opnået for et laminært grænselag på en tynd flad plade i en todimensional, parallel strømning af inkompressibel væske (figur 1). I dette tilfælde gør vurderingen af størrelsesordenen af ligningstermerne: x ~ L, y ~ δ, δ ~
det muligt at kombinere variablerne x og y i én relation
og at reducere løsningen af Eq. (8) (ved dp/dx = 0) til at bestemme afhængigheden af u og v af den nye parameter ξ. På den anden side er det ved hjælp af velkendte relationer mellem hastighedskomponenterne u, v og strømningsfunktionen ψ
det muligt at opnå én almindelig ikke-lineær differentialligning af tredje orden, i stedet for systemet af partielle differentialligninger (8)
Her er f(ξ) den ukendte funktion af variablen ξ: f = ƒ =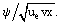
Den første numeriske løsning af Eq. (10) blev opnået af Blasius (1908) under randbetingelser, der svarer til de fysiske betingelser for grænselaget ved y = 0: u = 0, v = 0; ved y → ∞; u → Ue (Blasius’ grænselag).
Figur 2 sammenligner resultaterne af Blasius’ løsning (gennemgående linje) med eksperimentelle data. Ved hjælp af disse data er det muligt at vurdere det viskose grænselagstykkelse. Ved ξ 
2,5 er (u/Ue 0,99) (figur 2); ud fra Eq. (9) får vi følgelig:
Figur 2.
Fra de numeriske Blasius-beregninger af værdien af den anden afledte funktion af f(ξ) ved vægens gnidningsskubspænding er sammenhængen i dette tilfælde:
Friktionskraften R, der virker på begge sider af pladen med længde L (figur 1), bestemmes også fra Eq. (11):
som i friktionskoefficienten for flade plader:
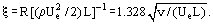
Trods det faktum, at Prandtl-ligningerne er meget enklere end Navier-Stokes-ligningerne, blev deres løsninger opnået for et begrænset antal problemer. For mange praktiske problemer er det ikke nødvendigt at bestemme hastighedsprofiler i grænselaget, men kun tykkelse og forskydningsspænding. Denne form for information kan opnås ved at løse den integrale impulsligning
Den integrale relation (12) gælder både for det laminære og det turbulente grænselag.
Funktioner, som ikke var kendt på forhånd, men som karakteriserer fordelingen af væskeparametre over lagtykkelsen δ, ligger under integralet i ligning (12). Og fejlen ved beregning af integralet er mindre end fejlen i den omtrentligt antagne integrandfunktion ρu = ρu(y). Dette skaber betingelser for udvikling af tilnærmede metoder til beregning af grænselagsparametre, som er mindre tidskrævende end de nøjagtige metoder til integrering af Prandtl-ligningerne. Det grundlæggende koncept blev først foreslået af T. von Karman, som indførte en sådan vilkårlig lagtykkelse δ*
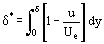
og impulsforskydningstykkelse δ**
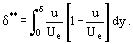
derved kan vi omdanne Eq. (12) for todimensionalt grænselag af inkompressibel væske til:
Der er tre ukendte funktioner i Eq. (15), nemlig δ* = δ*(x), δ** = δ**(x) og τw = τw(x) .
Løsningen af en ordinær differentialligning som Eq. (15) kræver normalt en antagelse (eller repræsentation) af hastighedsfordelingen (hastighedsprofil) over grænselagets tykkelse som funktion af nogle karakteristiske parametre (form-parametre), og det kræver også brug af empiriske data om forholdet mellem friktionskoefficienten Cf = 2τw/(ρU2e) og grænselagets vilkårlige tykkelse (friktionslov).
Der kan gives nogle bestemte fysiske forklaringer for så vidt angår værdierne af δ* og δ**. Integrandfunktionen i ligning (13) indeholder efter omlægning et udtryk (Ue – u), som karakteriserer hastighedsfaldet. Integralet i ligning (14) kan således betragtes som et mål for faldet i strømningshastigheden gennem grænselaget sammenlignet med den perfekte væskestrømning ved hastigheden Ue. På den anden side kan værdien af δ* betragtes som et mål for afvigelsen langs en normal til væggen (langs “y”-aksen) af den ydre strømningslinje under påvirkning af friktionskræfter. Ud fra denne betragtning af den integrale struktur i Eq. (14) kan man konkludere, at δ** karakteriserer impulsfaldet i grænselaget under påvirkning af friktion.
De følgende relationer er gyldige:
hvor H er formparameteren for grænselagets hastighedsprofil. For eksempel for lineær fordeling u = ky,
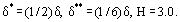
På nuværende tidspunkt anvendes såkaldte semi-empiriske teorier i vid udstrækning til forudsigelse af turbulente grænselagsparametre. I dette tilfælde antages det, at den samlede friktionsspænding τ i et turbulent grænselag er en sum
Her er τT den ekstra (turbulente eller Reynolds) friktionsspænding, især i en inkompressibel strømning
se Eq. (7).
Denne fremstilling er direkte forbundet med systemet af bevægelsesligninger i grænselaget (6). I det kompressible grænselag kan tæthedspulserne anses for at være resultatet af temperaturpulser
hvor β = (1/T) er den volumetriske ekspansionskoefficient.
Der anvendes yderligere semi-empiriske hypoteser om turbulent impulsoverførsel til at bestemme τT. F.eks.
hvor ηT er den dynamiske koefficient for turbulent viskositet, der blev indført af J. Boussinesq i 1877.
På grundlag af begrebet lighed mellem molekylær og turbulent udveksling (lighedsteori) indførte Prandtl hypotesen om blandingslængde (die Mischungsweg). Blandingslængden 1 er den vej, som et endeligt væskevolumen (“mol”) passerer fra et lag med gennemsnitlig bevægelse til et andet uden at ændre sin impuls. I overensstemmelse med denne betingelse udledte han en ligning, som viste sig at være grundlæggende for grænselagsteorien:
For det turbulente område af grænselaget i den nære vægs strømningsgrænse, L. Prandtl anså længden 1 for proportional med y
hvor κ er en empirisk konstant.
Tæt på væggen, hvor ηT << η, er viskøs molekylær friktion en afgørende faktor. Tykkelsen af denne del af grænselaget δ1, som er kendt som laminært eller viskøst underlag, er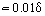
. Uden for underlaget stiger værdien af ηT og når op på flere størrelsesordener større end η. Tilsvarende er τT > 0 = η i denne zone af grænselaget, der er kendt som den turbulente kerne τT > 0 = η. Undertiden underopdeles den turbulente kerne i bufferzonen, hvor den laminære og turbulente friktion har samme værdi, og den udviklede zone, hvor τT >> τ0. For dette område er det efter integration af Eq. (18) og under hensyntagen til Eq. (19) muligt at udlede et udtryk for logaritmisk hastighedsprofil:
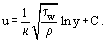
Hvis der anvendes dimensionsløse (eller universelle) koordinater:
hvor
er den såkaldte dynamiske hastighed (eller gnidningshastighed), Eq. (20) kan omskrives i følgende form:
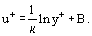
Velocity distribution representation in universal coordinates and mathematical models for turbulent viscosity coefficient are deated in more detail in the section of Turbulent Flow.
En af de nuværende versioner af den semi-empiriske teori for turbulente grænselag udviklet af S. S. Kutateladze og A. I. Leontiev er baseret på den såkaldte asymptotiske teori om turbulente grænselag ved Re → ∞ hvor tykkelsen af det laminære (viskose) underlag δ1 aftager med højere hastighed end δ som følge heraf (δ1/δ) → 0.
Under disse betingelser udvikler der sig et turbulent grænselag med “forsvindende viskositet”. I dette lag er η → 0, men er ikke lig med nul, og i denne henseende adskiller laget sig fra perfekt væskestrømning. Begrebet relativ friktionslov, der er indført af S. S. Kutateladze og A. I. Leontiev (1990), angiver
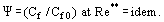
Loven er defineret som forholdet mellem friktionskoefficienten Cf for den pågældende tilstand og værdien af Cf0 for “standard”-forhold på en flad, uigennemtrængelig plade, der flyder rundt af en inkompressibel, isotermisk strømning, idet begge koefficienter fås for Re** = Ueδ**/ν. Det vises, at ved Re → ∞; η → 0; og Cf → 0 har den relative variation af friktionskoefficienten under indflydelse af sådanne forstyrrende faktorer som trykgradient, kompressibilitet, ikke-isotermi, injektion (sugning) gennem en porøs væg osv. en endelig værdi.
De afledte ligninger til beregning af værdien af Ψ har en vigtig egenskab, som gør Ψ uafhængig af empiriske turbulenskonstanter. I overensstemmelse med det grundlæggende begreb i den integrale “tilgang” omdannes den integrale impulsligning til:
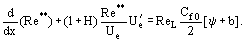
Her er 
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) permeabilitetsparametrene for det tilfælde, hvor en gas med densiteten ρw injiceres gennem en permeabel væg med hastigheden vw. Til bestemmelse af funktionen Re** = Re**
er det nødvendigt at beregne fordelingen
Til dette formål gælder princippet om superposition af forstyrrende faktorer
I Eq. 24 repræsenterer hver multiplikator den relative friktionslov, idet der tages hensyn til virkningen af en af faktorerne, blandt dem kompressibilitet ΨM, temperatur- (eller Enthalpy-) højde ΨT, injektion ΨB, trykgradient ΨP og andre.
De grundlæggende begreber for grænselaget skaber betingelser for at forklare sådanne fænomener som strømningsadskillelse fra overfladen under indflydelse af strømningens inerti, opbremsning af viskos strømning ved væggen og negativ trykgradient, der virker i opstrøms retning = 0 eller < 0.
Hvis trykgradienten er ugunstig på overfladen mellem sektionerne “1-4” (se figur 3), ændres hastighedsfordelingen u = u(x,y) i grænselaget gradvist; den bliver “mindre fuld”, idet hældningen aftager i de væskestråler, der er tættere på væggen og har mindre kinetisk energi (se hastighedsprofilformerne i figur 3), som trænger langt nedstrøms ind i området med øget tryk. I nogle afsnit, f.eks. afsnit “4”, bliver væskepartikler, der befinder sig på strømningslinjen “a-a” (stiplet linje i figur 3) – efter at have opbrugt deres kinetiske energi fuldstændigt – bremset (ua = 0).
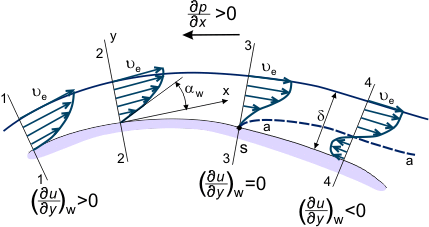
Figur 3. Grænselag i strømning over en dækket overflade.
Det statiske tryk og værdien af trykgradienten varierer ikke over grænselagets tykkelse. Derfor begynder væskepartikler, der er tættere på væggen end linje “a-a” og har endnu mindre energi, at bevæge sig i den modsatte retning under påvirkning af trykgradienten i afsnit “4-4” (se figur 3). Forholdet er således:
På denne måde ændres hastighedsprofilen på nogle steder på overfladen. Denne ændring er kendetegnet ved, at fortegnet på den afledte w ændres fra positivt (afsnit 2, figur 3) til negativt (afsnit 4). Det er naturligvis også muligt at definere det afsnit, hvor w = 0 (afsnit 3, figur 3). Dette kaldes grænselagsseparationsafsnittet (punkt “S” på overfladen af dette afsnit er separationspunktet). Det er kendetegnet ved udviklingen af en omvendt strømningszone – strømningen omkring legemet er ikke længere jævn, grænselaget bliver betydeligt tykkere, og de ydre strømningsstrømslinjer afviger fra overfladen af legemet, der flyves rundt om. Nedstrøms separationspunktet er den statiske trykfordeling over lagets tykkelse ikke stabil, og den statiske trykfordeling langs overfladen svarer ikke til trykfordelingen i den eksterne, inviskide strømning.
Separationen efterfølges af udviklingen af omvendte strømningszoner og hvirvler, hvor den kinetiske energi, der tilføres fra den eksterne strømning, omdannes til varme under indflydelse af friktionskræfter. Strømsseparationen, ledsaget af energidissipation i omvendt strømnings hvirvelzoner, resulterer i sådanne uønskede virkninger som forøgelse af flyvende køretøjers luftmodstand eller hydrauliske tab i kanaler.
På den anden side anvendes separerede strømninger i forskellige anordninger til intensiv blanding af væske (f.eks. for at forbedre blandingen af brændstof og luft i forbrændingskamre i motorer). Når viskose væsker strømmer i kanaler med variabelt tværsnit (vekslende trykgradient), kan separationszonen være lokal, hvis diffusorafsnittet efterfølges af konfusorafsnittet, hvor den separerede strøm igen vil knytte sig til overfladen (se figur 4a). Når strømningen adskilles fra legemets bagkant (f.eks. fra vingens bagkant), dannes det såkaldte kølvand ved “sammenkobling” af grænselagene (se figur 4b).
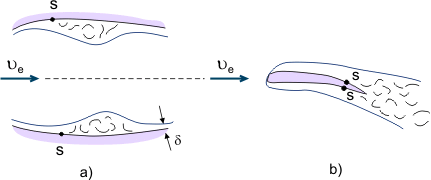
Figur 4. Grænselagsseparationsfænomener.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. og Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.