By Leave a Comment on Matematik for de frie fag

Nets

En sidste måde at repræsentere et fast stof på er ved at bruge et net. Hvis du klipper et net ud, kan du folde det sammen til en model af en figur. Nets kan også bruges til at analysere et enkelt fast stof. Her er et eksempel på et net til en terning.

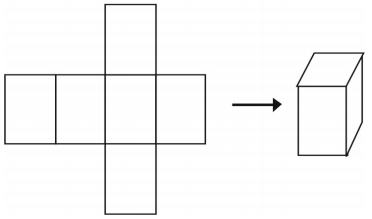
Der er mere end én måde at lave et net til en enkelt figur på.

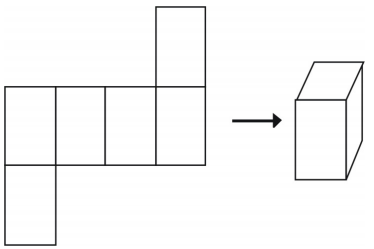
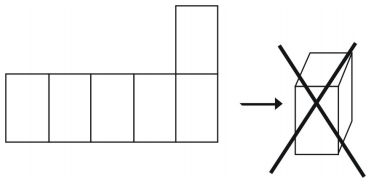
Det er dog ikke alle dispositioner, der skaber en terning.

Eksempel 1

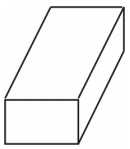
Hvilken slags figur skaber nettet? Tegn figuren.

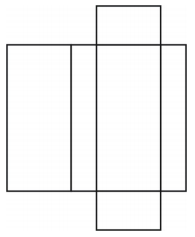
Nettet skaber et kasseformet rektangulært prisme som vist nedenfor.

Eksempel 2

Hvilken slags net kan du tegne for at repræsentere den viste figur? Tegn nettet.

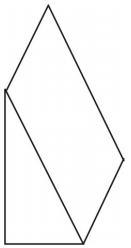
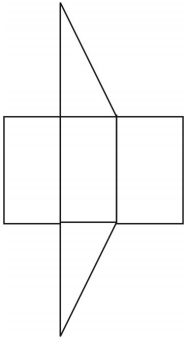
Der er vist et net til prismaet. Andre net er mulige.

Revisionsøvelser

Tegn et net for hver af følgende:

Svar

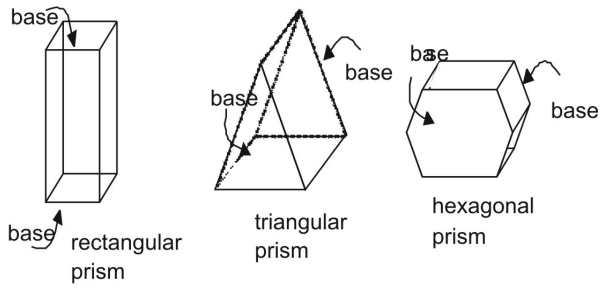
Prismer

En prisme er en tredimensionel figur med et par parallelle og kongruente ender, eller baser. Siderne i et prisme er parallelogrammer. Prismer identificeres ved deres baser.

Overfladeareal af et prisme ved hjælp af net

Prismerne ovenfor er retvinklede prismer. I et retvinklet prisme er sidesiderne vinkelrette på prismaets baser. Sammenlign et retvinklet prisme med et skråt prisme, hvor sider og baser ikke er vinkelrette.

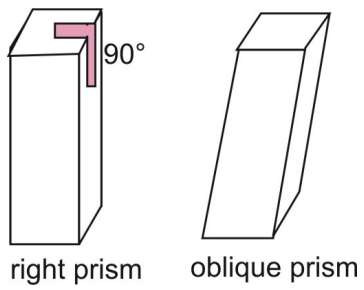
To postulater, der gælder for areal, er arealkongruenspostulatet og arealadditionspostulatet.

Arealkongruenspostulatet: Hvis to polygoner (eller plane figurer) er kongruente, er deres arealer også kongruente.
Arealadditionspostulat:

Du kan bruge et net og arealadditionspostulatet til at finde overfladearealet af et retvinklet prisme ved hjælp af et net og arealadditionspostulatet.

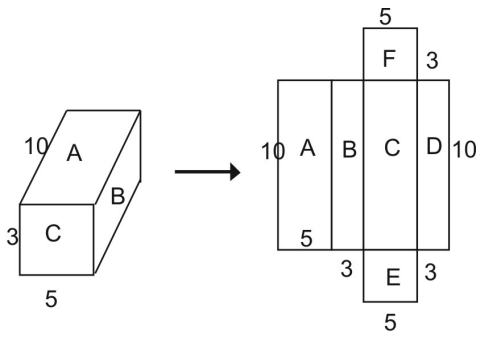
Fra nettet kan du se, at hele prismaets overfladeareal er lig med summen af de figurer, der indgår i nettet:

Totalt overfladeareal = areal A + areal B + areal C + areal D + areal E + areal F

Hvis du bruger formlen for arealet af et rektangel, kan du se, at arealet af rektangel A er:

A = l – w
A = 10 – 5 = 50 kvadratiske enheder

På samme måde indsættes arealerne af de andre rektangler tilbage i ligningen ovenfor.

Totalt areal = areal A + areal B + areal C + areal D + areal E + areal F
Totalt areal = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3) + (5 – 3)
Totalt overfladeareal = 50 + 30 + 50 + 30 + 30 + 15 + 15
Totalt overfladeareal = 190 kvadratiske enheder

Eksempel 3

Brug et net til at finde overfladearealet af prismet.

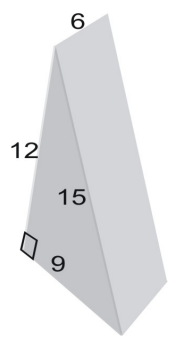
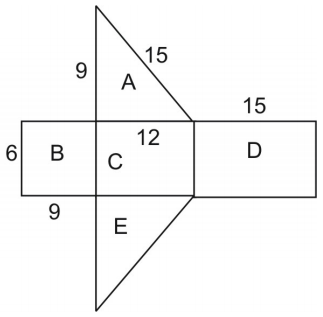
Nettets areal er lig med figurens overfladeareal. For at finde arealet af trekanten bruger vi formlen:

\displaystyle{A}=\frac{1}{2}hb\\\\ hvor h er højden af trekanten og b er dens base.

Bemærk, at trekanterne A og E er kongruente, så vi kan gange arealet af trekant A med 2.

\displaystyle\text{area}=\text{area }A+\text{area }B+\text{area }C+\text{area }D+\text{area }D+\text{area }E\\
\displaystyle\text{ }=2(\text{area }A)+\text{area }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\

Thus, er overfladearealet 324 kvadrat-enheder.

Revisionsøvelser

For hver af følgende finder du overfladen er a ved hjælp af netmetoden og omkredsen

  3. Basen af et prisme er en retvinklet trekant, hvis ben er 3 og 4, og vis højden er 20. Hvad er det samlede areal af prismet?
  5. Et ret sekskantet prisme er 24 tommer højt og har baser, der er regelmæssige sekskanter, der måler 8 tommer på en side. Hvad er det samlede overfladeareal?
  6. Hvad er volumenet af prismet i opgave 4?

I følgende spørgsmål er en lade formet som et femkantet prisme med dimensioner angivet i fod:

  1. Hvor mange kvadratfod (eksklusive taget) er der på overfladen af den lade, der skal males?
  2. Hvis en gallon maling dækker 250 kvadratfod, hvor mange galloner maling skal der så bruges til at male laden?
  3. En papkasse er en perfekt terning med en kant på 17 tommer. Hvor mange kubikfod kan den rumme?
  4. En swimmingpool er 16 fod bred, 32 fod lang og er ensartet 4 fod dyb. Hvor mange kubikfod vand kan den rumme?
  5. En kornæske har en længde på 25 cm, en bredde på 9 cm og en højde på 30 cm. Hvor meget cornflakes kan den indeholde?

Svar

Net og omkreds:

  1. 40,5 in2
  2. 838 cm2
  3. 252 kvadrat enheder
  4. 1484.6 kvadrat enheder
  5. 3990,7 kubik tommer

Laden:

  1. 2450 kvadratfod
  2. 10 gallon maling
  3. 2,85 kubikfod (vær forsigtig her. Enhederne i opgaven er angivet i tommer, men spørgsmålet spørger efter fødder.)
  4. 2048 kubikfod
  5. 6750 cm3

Cylindre

En cylinder er en tredimensionel figur med et par parallelle og kongruente cirkulære ender, eller baser. En cylinder har en enkelt buet side, der danner et rektangel, når den er lagt fladt ud.

Som med prismer kan cylindere være retvinklede eller skråvinklede. Siden på en ret cylinder er vinkelret på dens cirkulære baser. Siden af en skrå cylinder er ikke vinkelret på dens baser.

Overfladeareal af en cylinder ved hjælp af net

Du kan dekonstruere en cylinder til et net.

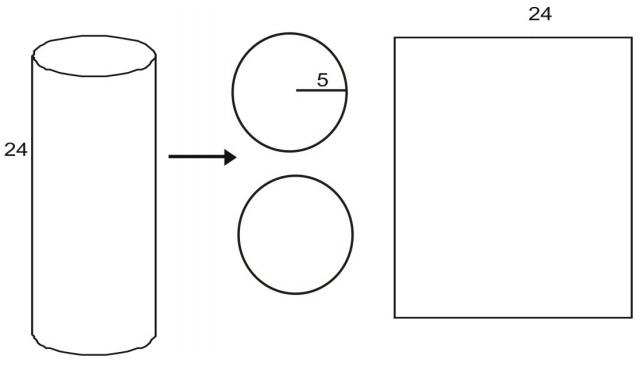
Overfladen af hver bund er givet ved arealet af en cirkel:

A=\pi{r}^2\\
A=\pi(5)^2\\
A=25\pi\
A\approx(25)(3,14)=78,5\\

Overfladen af det rektangulære sideareal L er givet ved produktet af en bredde og en højde. Højden er givet som 24. Du kan se, at bredden af arealet er lig med omkredsen af den cirkulære bund.

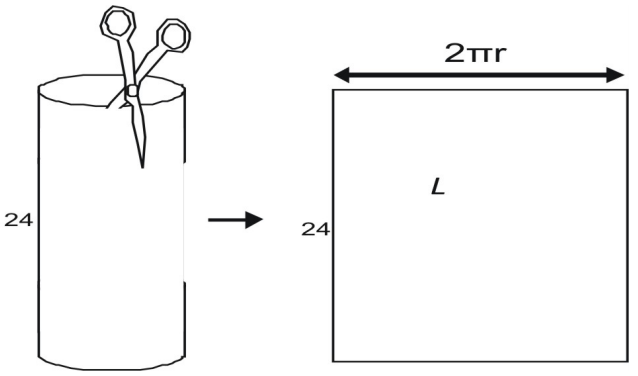
For at finde bredden skal du forestille dig at tage en dåselignende cylinder fra hinanden med en saks. Når du klipper sidearealet, ser du, at det er lig med omkredsen af dåsens top. Omkredsen af en cirkel er givet ved C = 2πr, det laterale areal, L, er

L=2{\pi}rh\\
L=2{\pi}(5)(24)\\
L=240\pi\\
L\approx(240)(3.14)=753,6\\\

Nu kan vi finde arealet af hele cylinderen ved at bruge A = (areal af de to baser) + (areal af den laterale side).

A=2(75,36)+753,6\\
A=904,32\

Du kan se, at den formel, vi brugte til at finde det samlede overfladeareal, kan bruges for en hvilken som helst ret cylinder.

Areal af en ret cylinder: En ret cylinders overfladeareal med radius og højde h er givet ved A = 2B + L, hvor B er arealet af hver bund i cylinderen, og L er cylinderens sideareal.

Eksempel 4

Brug et net til at finde cylinderens overfladeareal.

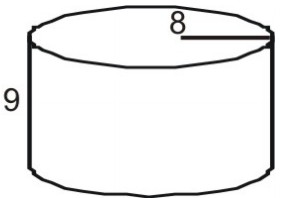
Tegn og mærk først et net til figuren.

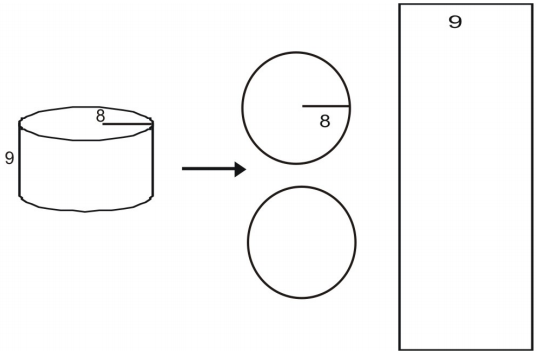
Beregn arealet af hver base.

A=\pi{r}^2\\
A=\pi(8)^2\
A=\pi(8)^2\
A=64\pi\\
A\approx(64)(3.14)=200.96\\

Calculate L.

L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16\\\

Find arealet af hele cylinderen.

A=2(200.96)+452.16\\
A=854.08\\

Dermed er det samlede overfladeareal ca. 854,08 kvadrat enheder

Overfladeareal af en cylinder ved hjælp af en formel

Du har set, hvordan du kan bruge net til at finde det samlede overfladeareal af en cylinder. Postulatet kan nedbrydes for at skabe en generel formel for alle rette cylindre.

A = 2B + L

Bemærk, at grundarealet, B, for en hvilken som helst cylinder er: B = πr2

Det laterale areal, L, for en hvilken som helst cylinder er: B = πr2

L=\text{bredde af sidearealet}\cdot\text{højde af cylinderen}\\
L=\text{omkreds af basen}\cdot\text{højde af cylinderen}\\
L=2\pi{r}\cdot{h}\\

Sætter vi de to ligninger sammen, får vi:

Gennemregning af a fra ligningen giver:

Overfladearealet af en ret cylinder: En ret cylinder med radius r og højde h kan udtrykkes som:

A = 2πr2 + 2πrh

eller:

A = 2πr(r + h)

Du kan bruge formlerne til at finde arealet af en hvilken som helst ret cylinder.

Eksempel 5

Brug formlen til at finde cylinderens overfladeareal.

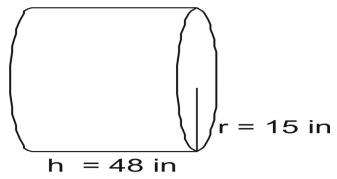
Skriv formlen og indsæt værdierne, og løs den.

A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\text{ kvadratcentimeter}\\\

Eksempel 6

Find cylinderens overfladeareal.

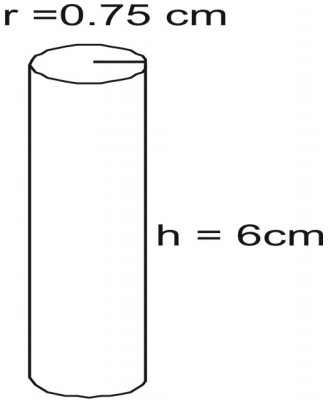
Skriv formlen og indsæt værdierne, og løs den.

A=2\pi{r}(r+h)\\
A=2(3,14)(0,75)\\
A=31.7925\text{ kvadratcentimeter}\\\

Eksempel 7

Find højden på en cylinder, der har en radius på 4 cm og et overfladeareal på 226,08 kvadratcentimeter.

Skriv formlen med de givne oplysninger, og løs h.

A=2\pi{r}(r+h)\\
226,08=2(3,14)(4)\\
226,08=25,12\
226,08=100,48+25,12h\\
5=h\\\

Sfærer

En kugle er en tredimensionel figur, der har form som en kugle.

Sfærer kan karakteriseres på tre måder.

  • En kugle er mængden af alle punkter, der ligger i en fast afstand r fra et enkelt centrumpunkt O.
  • En kugle er den overflade, der opstår, når en cirkel roteres om en af dens diametre.

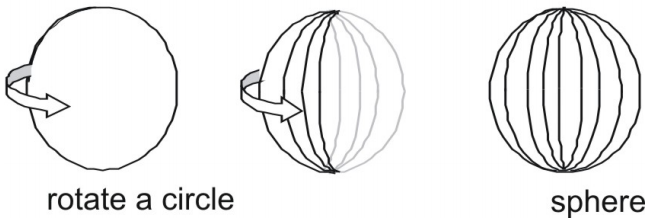
Overfladeareal af en kugle

Man kan udlede formlen for en kugles overfladeareal ved at foretage målinger af kugler og cylindre. Her viser vi en kugle med en radius på 3 og en ret cylinder med både en radius og en højde på 3 og udtrykker arealet i π.

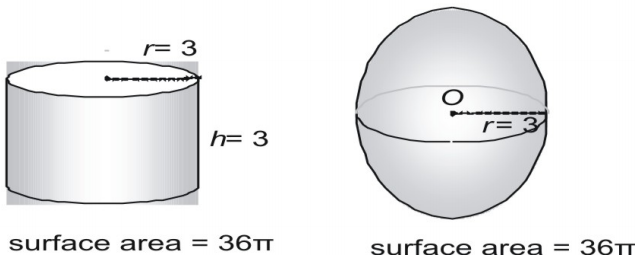
Prøv nu et større par, hvor du udtrykker overfladearealet i decimalform.

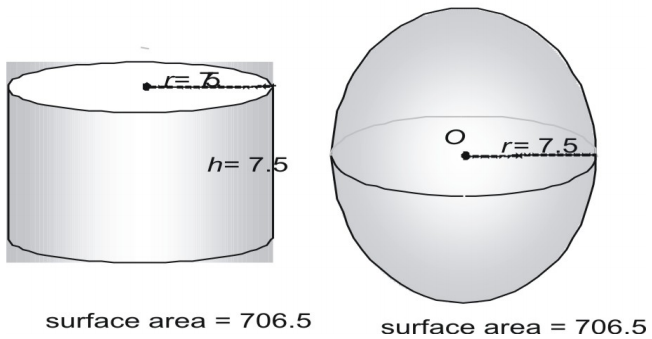
Se på et tredje par.

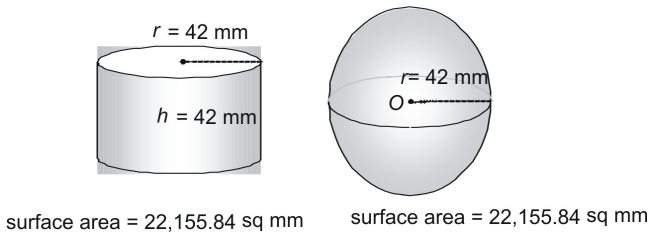
Er det et tilfælde, at en kugle og en cylinder, hvis radius og højde er lig med kuglens radius, har nøjagtig samme overfladeareal? Overhovedet ikke! Faktisk brugte de gamle grækere en metode, der viste, at følgende formel kan bruges til at finde overfladearealet af en hvilken som helst kugle (eller en hvilken som helst cylinder, hvori ).

Overfladearealet af en kugle er givet ved: A = 4πr2

Eksempel 8

Find overfladearealet af en kugle med en radius på 14 fod.

Anvend formlen.

A=4\pi{r}^2\\
A=4\pi(14)^2\\
A=4\pi(14)^2\
A=4\pi(196)\\
A=784\pi\\
2461.76\text{ kvadratfod ved hjælp af }3.14\text{ for }\pi\\\\

Eksempel 9

Find overfladearealet af følgende figur med π som udtryk for π.

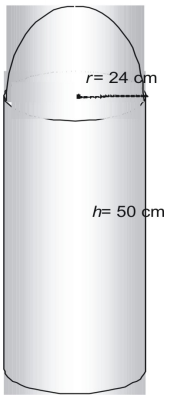
Figuren består af en halvkugle eller halvkugle og en cylinder uden top.

A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half kugle})=2\pi(576)\\
A(\text{halvkugle})=1152\pi\text{ kvadrat cm}\\

Find nu arealet af cylinderen uden dens top.

A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\

Thus, er det samlede overfladeareal 1152\pi+2976\pi=4128\pi\\\

Revisionsøvelser

  1. Find radius af den kugle, der har et rumfang på 335 cm3.
  2. Bestem overfladearealet og rumfanget af denne form:
  3. Radius af en kugle er 4. Find dens rumfang og samlede overfladeareal.
  4. En kugle har en radius på 5. En ret cylinder, der har samme radius, har det samme rumfang. Find cylinderens højde og samlede overfladeareal.
  5. Sfære: rumfang = 296 cm3. Find diameteren.
  6. Sfære: overfladearealet er 179 in2. Find radius.
  7. Tennisbolde med en diameter på 3,5 tommer sælges i dåser med tre stk. Dåsen er en cylinder. Antag, at boldene berører dåsen på siderne, i toppen og i bunden. Hvad er rumfanget af det rum, der ikke er optaget af tennisboldene?
  8. En kugle har et overfladeareal på 36π in2. Find dens rumfang.
  9. En gigantisk skovl, der betjenes af en kran, har form som en halvkugle med radius = 21 tommer. Skovlen er fyldt med smeltet varmt stål. Når stålet hældes i en cylindrisk lagertank, der har en radius på 28 tommer, vil det smeltede stål stige op til en højde på hvor mange tommer?

Svar

Bemærk, at der i disse opgaver anvendes π og ikke 3,14.

  1. 1. Radius = 4,31 cm
  2. Overfladeareal = 706,86 cm2
    Volumen = 1767,15 cm3
  3. Volumen = 268,08 enheder3
    Overfladeareal = 201,06 enheder2
  4. Højde = 20/3 enheder samlet overfladeareal = 366,52 enheder2
  5. Diameter = 8,27cm
  6. Radius = 3.77 tommer
  7. Volumen af cylinder = 32,16π in3 volumen af tennisbolde = 21,44π in3
    Volumen af det rum, der ikke er optaget af tennisbolde = 33,68 in3
  8. Volumen = 113,10 in3
  9. Højden af smeltet stål i cylinderen vil være 7,88 tommer

Skriv et svar

Din e-mailadresse vil ikke blive publiceret.