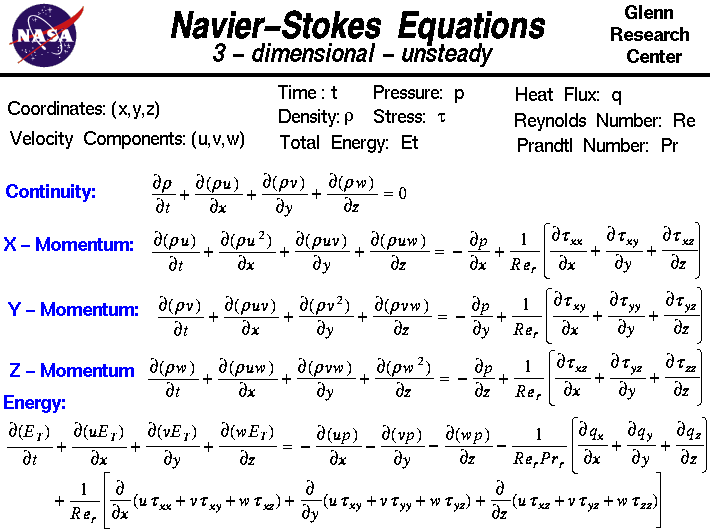
På dette dias viser vi den tredimensionelle ustabile form af Navier-Stokes-ligningerne.Disse ligninger beskriver, hvordan hastighed, tryk, temperatur og massefylde af en flydende væske i bevægelse hænger sammen.Ligningerne blev udledt uafhængigt af G.G. Stokes i England og M. Navier i Frankrig i begyndelsen af 1800-tallet.Ligningerne er en udvidelse af Euler-ligningerne og omfatter viskositetens indvirkning på strømningen.Disse ligninger er meget komplekse, men ingeniørstuderende lærer at udlede dem i en proces, der minder meget om den udledning, som vi præsenterer på websiden om bevarelse af momentum.
Ligningerne er et sæt koblede differentialligninger og kunne i teorien løses for et givet strømningsproblem ved hjælp af metoder fra regning.Men i praksis er disse ligninger for vanskelige at løse analytisk.Tidligere foretog ingeniører yderligere tilnærmelser og forenklinger af ligningssættet, indtil de havde en gruppe af ligninger, som de kunne løse.For nylig er højhastighedscomputere blevet brugt til at løse tilnærmelser til ligningerne ved hjælp af en række teknikker som finite differencer, finite mængder, finite elementer og spektralmetoder.Dette studieområde kaldes Computational Fluid Dynamics eller CFD.
Navier-Stokes-ligningerne består af en tidsafhængig kontinuitetsligning for bevarelse af masse, tre tidsafhængige momentbevaringsligninger og en tidsafhængig energibeskyttelsesligning.Der er fire uafhængige variabler i problemet, de rumlige koordinaterx, y og z for et område og tiden t. Der er seks afhængige variabler; trykket p, densiteten r og temperaturen T (som er indeholdt i energiligningen gennem den samlede energi Et) og tre komponenter af hastighedsvektoren; u-komponenten er i x-retningen, v-komponenten er i y-retningen, og w-komponenten er i z-retningen.Alle de afhængige variabler er funktioner af alle fire uafhængige variabler.Differentialligningerne er derfor partielle differentialligningerog ikke de almindelige differentialligninger, som du studerer i en begyndende regnetime.
Du vil bemærke, at differentialsymbolet er anderledes end de sædvanlige “d /dt” eller “d /dx”, som du ser for almindelige differentialligninger. Symbolet “
” bruges til at angive partielle afledninger.Symbolet angiver, at vi skal holde alle de uafhængige variabler faste, undtagen variablen ved siden af symbolet, når vi beregner en afledning. Ligningssættet er:
Kontinuitet: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momentum: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Momentum: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momentum: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energi: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
hvor Re erReynolds-tallet, som er en lighedsparameter, der er forholdet mellem skalaen af strømningens inerti og de viskose kræfter i strømningen. q-variablerne er varmestrømskomponenterne, og Pr er Prandtl-tallet, som er en lighedsparameter, der er forholdet mellem de viskose spændinger og de termiske spændinger.tau-variablerne er komponenter af spændingstensorerne.En tensor dannes, når man multiplicerer to vektorer på en bestemt måde. Vores hastighedsvektor har tre komponenter; spændingstensor har ni komponenter. Hver komponent af spændingstensoren er i sig selv en anden afledt af hastighedskomponenterne.
Termerne på venstre side af impulsligningerne kaldes ligningernes konvektionstermer.Konvektion er en fysisk proces, der forekommer i en gasstrøm, hvor en eller anden egenskab transporteres ved strømningens ordnede bevægelse.De termer på højre side af impulsligningerne, der multipliceres med det omvendte Reynoldstal, kaldes diffusionstermerne.Diffusion er en fysisk proces, der finder sted i en gasstrømning, hvor en egenskab transporteres gennem gasmolekylernes tilfældige bevægelse.Diffusion er relateret til spændingstensoren og til gassens viskositet. Turbulens og dannelsen af grænselag er et resultat af diffusion i strømningen. Euler-ligningerne indeholder kun konvektionstermerne i Navier-Stokes-ligningerne og kan derfor ikke modellere grænselag. Der findes en særlig forenkling af Navier-Stokesligningerne, som beskriver grænselagsstrømme.
Bemærk, at alle de afhængige variabler optræder i hver ligning.For at løse et strømningsproblem skal man løse alle fem ligninger samtidig; det er derfor, vi kalder dette et koblet ligningssystem.Der er faktisk nogle andreligninger, som er nødvendige for at løse dette system. Vi viser kun fem ligninger for seks ubekendte. En tilstandsligning relaterer gassens tryk, temperatur og densitet.Og vi skal specificere alle termerne i spændingstensorerne.I CFD tilnærmes spændingstensorerne ofte ved hjælp af en turbulencemodel.
Aktiviteter:
Guidede ture
Navigation ..
Begyndervejledning Home Page