Una capa límite es una fina capa de fluido viscoso cerca de la superficie sólida de una pared en contacto con una corriente en movimiento en la que (dentro de su espesor δ) la velocidad del flujo varía desde cero en la pared (donde el flujo se «pega» a la pared debido a su viscosidad) hasta Ue en el límite, que corresponde aproximadamente (con un error del 1%) a la velocidad de la corriente libre (véase la figura 1). En sentido estricto, el valor de δ es un valor arbitrario porque la fuerza de fricción, que depende de la interacción molecular entre el fluido y el cuerpo sólido, disminuye con la distancia a la pared y se hace igual a cero en el infinito.
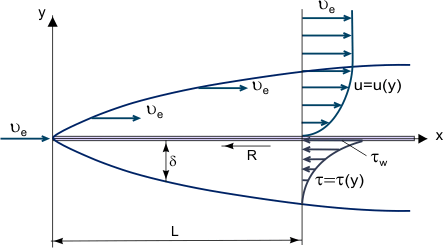
Figura 1. Crecimiento de una capa límite en una placa plana.
El concepto fundamental de la capa límite fue sugerido por L. Prandtl (1904), define la capa límite como una capa de fluido que se desarrolla en flujos con números de Reynolds muy altos Re, es decir con una viscosidad relativamente baja en comparación con las fuerzas de inercia. Esto se observa cuando los cuerpos están expuestos a una corriente de aire de alta velocidad o cuando los cuerpos son muy grandes y la velocidad de la corriente de aire es moderada. En este caso, en una capa límite relativamente delgada, la tensión de cizallamiento por fricción (fuerza de cizallamiento viscosa): τ = η (donde η es la viscosidad dinámica; u = u(y) – «perfil» de la componente de la velocidad longitudinal de la capa límite, véase la figura 1) puede ser muy grande; en particular, en la pared donde u = 0 y τw = ηw aunque la propia viscosidad puede ser bastante pequeña.
Es posible ignorar las fuerzas de fricción fuera de la capa límite (en comparación con las fuerzas de inercia), y sobre la base del concepto de Prandtl, considerar dos regiones de flujo: la capa límite donde los efectos de fricción son grandes y el núcleo de flujo casi Inviscid. Partiendo de la premisa de que la capa límite es una capa muy fina (δ << L, donde L es la dimensión lineal característica del cuerpo sobre el que se produce el flujo o del canal que lo contiene, siendo su espesor decreciente con el crecimiento de Re, Figura 1), se puede estimar el orden de magnitud del espesor de la capa límite a partir de la siguiente relación
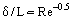
Por ejemplo, cuando un avión vuela a Ue = 400 km/h, el espesor de la capa límite en el borde de salida del ala con 1 metro de cuerda (longitud del perfil) es de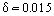
m. Como se ha establecido experimentalmente, se desarrolla una capa límite laminar en la sección de entrada del cuerpo. Gradualmente, bajo la influencia de algunos factores desestabilizadores, la capa límite se vuelve inestable y tiene lugar la transición de la capa límite a un régimen de flujo turbulento. Investigaciones experimentales especiales han establecido la existencia de una región de transición entre las regiones turbulenta y laminar. En algunos casos (por ejemplo, con un alto nivel de turbulencia del flujo externo), la capa límite se vuelve turbulenta inmediatamente después del punto de estancamiento del flujo. En algunas condiciones, como una fuerte caída de presión, se produce un fenómeno inverso en los flujos turbulentos acelerados, a saber, la relaminarización del flujo.
A pesar de su relativa delgadez, la capa límite es muy importante para iniciar procesos de interacción dinámica entre el flujo y el cuerpo. La capa límite determina la resistencia aerodinámica y la sustentación del vehículo en vuelo, o la pérdida de energía para el flujo de fluidos en los canales (en este caso, una capa límite hidrodinámica porque también hay una capa límite térmica que determina la interacción termodinámica de Transferencia de Calor).
El cálculo de los parámetros de la capa límite se basa en la solución de las ecuaciones obtenidas a partir de las ecuaciones de Navier-Stokes para el movimiento de los fluidos viscosos, que primero se simplifican considerablemente teniendo en cuenta la delgadez de la capa límite.
La solución propuesta por L. Prandtl es esencialmente el primer término de la expansión en serie de potencias de la ecuación de Navier-Stokes, realizándose la expansión en serie para potencias del parámetro adimensional (δ/L). El parámetro más pequeño de este término está en potencia cero, de modo que la ecuación de la capa límite es la aproximación cero en una expansión asintótica (a gran Re) de la ecuación de la capa límite (solución asintótica).
Una transformación de la ecuación de Navier-Stokes en las ecuaciones de la capa límite puede demostrarse derivando la ecuación de Prandtl para la capa límite laminar en un flujo incompresible bidimensional sin fuerzas del cuerpo.
En este caso, el sistema de ecuaciones de Navier-Stokes será:
Después de evaluar el orden de magnitud de algunos términos de la Ec. (2) e ignorando los términos pequeños, el sistema de ecuaciones de Prandtl para la capa límite laminar se convierte en:
en el que x, y son coordenadas longitudinales y laterales (Figura 1); v es la componente de la velocidad a lo largo del eje «y»; p, la presión; t, el tiempo; y n la viscosidad cinemática.
La capa límite es delgada y la velocidad en su borde externo Ue puede determinarse de forma suficiente y precisa como la velocidad de un flujo de fluido ideal (no viscoso) a lo largo de la pared calculada hasta la primera aproximación, sin tener en cuenta la acción inversa de la capa límite sobre el flujo externo. El gradiente de presión longitudinal = (en p(y) = const) en la ecuación (3) puede representarse a partir de la ecuación de Euler del movimiento de un fluido ideal. A partir de lo anterior, las ecuaciones de Prandtl en su forma finita se escribirán como:
Se trata de un sistema de ecuaciones diferenciales parabólicas parciales no lineales de segundo orden que se resuelven con condiciones iniciales y de contorno
El sistema de ecuaciones (4) se escribe para valores reales de las componentes de la velocidad u y v. Para generalizar las ecuaciones obtenidas para el flujo turbulento, se debe utilizar la conocida relación entre los parámetros de las componentes reales, promediadas y pulsantes de los flujos turbulentos. Por ejemplo, para los componentes de velocidad existen relaciones que conectan los componentes reales u y v, los promediados ū y
y los pulsantes u’ y v’:
Tras algunos reordenamientos, es posible obtener otro sistema de ecuaciones a partir del sistema (3), en particular para el flujo estacionario:
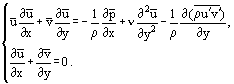
Utilizando la siguiente relación para el esfuerzo cortante de fricción en la capa límite:
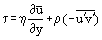
y teniendo en cuenta que en la capa límite laminar u = u’ y
es posible reescribir las ecuaciones de Prandtl en una forma válida tanto para flujos laminares como turbulentos:
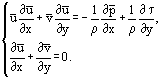
Las soluciones más sencillas se han obtenido para una capa límite laminar sobre una placa plana delgada en un flujo bidimensional y paralelo de fluido incompresible (Figura 1). En este caso, la estimación del orden de magnitud de los términos de las ecuaciones: x ~ L, y ~ δ, δ ~
permite combinar las variables x e y en una sola relación
y reducir la solución de la Ec. (8) (a dp/dx = 0) a la determinación de las dependencias de u y v respecto al nuevo parámetro ξ. Por otra parte, utilizando relaciones bien conocidas entre las componentes de la velocidad u, v y la función de flujo ψ
es posible obtener una ecuación diferencial ordinaria no lineal de tercer orden, en lugar del sistema de ecuaciones diferenciales parciales (8)
Aquí, f(ξ) es la función desconocida de variable ξ: f = ƒ =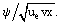
La primera solución numérica de la Ec. (10) fue obtenida por Blasius (1908) en condiciones de contorno correspondientes a las condiciones físicas de la capa límite en y = 0: u = 0, v = 0; en y → ∞; u → Ue (capa límite de Blasius).
La figura 2 compara los resultados de la solución de Blasius (línea continua) con los datos experimentales. Utilizando estos datos, es posible evaluar el espesor de la capa límite viscosa. A ξ 
2,5, (u/Ue 0,99) (Figura 2); en consecuencia, a partir de la Ec. (9) se obtiene:
Figura 2.
A partir de los cálculos numéricos de Blasius del valor de la segunda derivada de la función f(ξ) en el esfuerzo cortante de fricción de la pared, la relación en este caso es:
La fuerza de fricción R, que actúa en ambos lados de la placa de longitud L (Figura 1), se determina también a partir de la Ec. (11):
como en el coeficiente de fricción para placas planas:
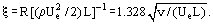
A pesar de que las ecuaciones de Prandtl son mucho más sencillas que las de Navier-Stokes, sus soluciones se obtuvieron para un número limitado de problemas. Para muchos problemas prácticos, no es necesario determinar los perfiles de velocidad en la capa límite, sólo el espesor y el esfuerzo cortante. Este tipo de información puede obtenerse resolviendo la ecuación integral del momento
La relación integral (12) es válida tanto para la capa límite laminar como para la turbulenta.
Las funciones que no se conocían a priori pero que caracterizan la distribución de los parámetros del fluido a lo largo del espesor de la capa δ están bajo la integral de la Ec. (12). Y el error de cálculo de la integral es menor que el error en la función integrante aproximadamente asumida ρu = ρu(y). Esto crea condiciones para el desarrollo de métodos aproximados de cálculo de los parámetros de la capa límite que consumen menos tiempo que los métodos exactos de integración de las ecuaciones de Prandtl. El concepto fundamental fue sugerido por primera vez por T. von Karman, quien introdujo dicho espesor de capa arbitrario δ*
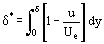
y el espesor de desplazamiento del momento δ**
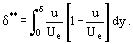
así, podemos transformar la Ec. (12) para una capa límite bidimensional de fluido incompresible a:
Hay tres funciones desconocidas en la Ec. (15), a saber, δ* = δ*(x), δ** = δ**(x) y τw = τw(x) .
La solución de una ecuación diferencial ordinaria como la Ec. (15) suele requerir la suposición (o representación) de la distribución de la velocidad (perfil de velocidad) a lo largo del espesor de la capa límite en función de algunos parámetros característicos (parámetros de forma), y también requiere el uso de datos empíricos sobre la relación entre el coeficiente de fricción Cf = 2τw/(ρU2e) y el espesor arbitrario de la capa límite (ley de fricción).
Pueden darse algunas explicaciones físicas definitivas en cuanto a los valores de δ* y δ**. La función integrante en la Ecuación (13) contiene, después de un reordenamiento, un término (Ue – u) que caracteriza la disminución de la velocidad. La integral de la Ecuación (14) puede considerarse, por tanto, como una medida de la disminución del flujo a través de la capa límite, en comparación con el flujo de fluido perfecto a la velocidad Ue. Por otra parte, el valor de δ* puede considerarse como la medida de la desviación a lo largo de una normal a la pared (a lo largo del eje «y») de la línea de flujo externa bajo la influencia de las fuerzas de fricción. De esta consideración de la estructura integral de la Ec. (14), es posible concluir que δ** caracteriza la disminución del momento en la capa límite bajo la influencia de la fricción.
Las siguientes relaciones son válidas:
donde H es el parámetro de forma del perfil de velocidad de la capa límite. Por ejemplo, para una distribución lineal u = ky,
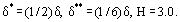
En la actualidad, las llamadas teorías semiempíricas se utilizan ampliamente para predecir los parámetros de la capa límite turbulenta. En este caso, se supone que la tensión de fricción total τ en una capa límite turbulenta es una suma
Aquí, τT es la tensión de fricción adicional (turbulenta o de Reynolds), en particular, en un flujo incompresible
véase la Ec. (7).
Esta representación está directamente conectada con el sistema de ecuaciones de movimiento en la capa límite (6). En la capa límite compresible, las pulsaciones de densidad pueden considerarse el resultado de las pulsaciones de temperatura
donde β = (1/T) es el coeficiente de expansión volumétrica.
Para determinar τT se utilizan hipótesis semiempíricas adicionales sobre la transferencia de momento turbulento. Por ejemplo,
donde ηT es el coeficiente dinámico de viscosidad turbulenta introducido por J. Boussinesq en 1877.
Sobre la base del concepto de similitud del intercambio molecular y turbulento (teoría de la similitud) Prandtl introdujo la hipótesis de la longitud de mezcla (die Mischungsweg). La longitud de mezcla 1 es el camino que recorre un volumen finito de fluido («mol») de una capa de movimiento medio a otra sin cambiar su momento. De acuerdo con esta condición, derivó una ecuación que resultó ser fundamental para la teoría de la capa límite:
Para la región turbulenta de la capa límite del flujo cercano a la pared, L. Prandtl consideró la longitud 1 proporcional a y
donde κ es una constante empírica.
Cerca de la pared, donde ηT << η, la fricción molecular viscosa es un factor determinante. El espesor de esta parte de la capa límite δ1, que se conoce como subcapa laminar o viscosa, es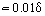
. Fuera de la subcapa, el valor de ηT aumenta, alcanzando varios órdenes de magnitud mayores que η. En consecuencia, en esta zona de la capa límite conocida como núcleo turbulento τT > 0 = η. A veces el núcleo turbulento se subdivide en la zona de amortiguación, donde la fricción laminar y turbulenta tienen el valor comparable, y la zona desarrollada, donde τT >> τ0. Para esta región, después de integrar la Ec. (18) y teniendo en cuenta la Ec. (19), es posible derivar una expresión para el perfil de velocidad logarítmica:
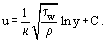
Si se utilizan coordenadas adimensionales (o universales).
donde
es la llamada velocidad dinámica (o velocidad de fricción), la Ec. (20) puede reescribirse de la siguiente forma:
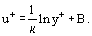
La representación de la distribución de la velocidad en coordenadas universales y los modelos matemáticos para el coeficiente de viscosidad turbulenta se tratan con más detalle en la sección de Flujo Turbulento.
Una de las versiones actuales de la teoría semiempírica de la capa límite turbulenta desarrollada por S. S. Kutateladze y A. I. Leontiev se basa en la llamada teoría asintótica de las capas límite turbulentas en Re → ∞ donde el espesor de la subcapa laminar (viscosa) δ1 disminuye a un ritmo mayor que δ como resultado de lo cual (δ1/δ) → 0.
En estas condiciones, se desarrolla una capa límite turbulenta con «viscosidad evanescente». En esta capa, η → 0 pero no es igual a cero y, en este sentido, la capa difiere del flujo de fluido perfecto. El concepto de ley de fricción relativa, introducido por S. S. Kutateladze y A. I. Leontiev (1990), indica
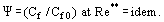
La ley se define como la relación entre el coeficiente de fricción Cf para la condición considerada y el valor de Cf0 para condiciones «estándar» en una placa plana e impermeable volada por un flujo incompresible e isotérmico, obteniéndose ambos coeficientes para Re** = Ueδ**/ν. Se demuestra que en Re → ∞; η → 0; y Cf → 0, la variación relativa del coeficiente de fricción bajo la influencia de factores perturbadores como el gradiente de presión, la compresibilidad, la no isotermicidad, la inyección (succión) a través de una pared porosa, etc., tiene un valor finito.
Las ecuaciones derivadas para calcular el valor de Ψ tienen una característica importante que hace que Ψ sea independiente de las constantes empíricas de la turbulencia. De acuerdo con el concepto fundamental de la «aproximación» integral, la ecuación integral del momento se transforma en:
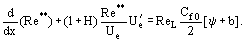
Aquí,
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) son los parámetros de permeabilidad para el caso de inyectar un gas a densidad ρw a través de una pared permeable a la velocidad de vw. Para determinar la función Re** = Re**
, es necesario calcular la distribución
Para ello, se aplica el principio de superposición de factores perturbadores
En la Ec. 24, cada multiplicador representa la ley de fricción relativa, teniendo en cuenta el efecto de uno de los factores, entre ellos la compresibilidad ΨM, la cabeza de temperatura (o Entalpía) ΨT, la inyección ΨB, el gradiente de presión ΨP y otros.
Los conceptos fundamentales de la capa límite crean condiciones para explicar fenómenos como la separación del flujo de la superficie bajo la influencia de la inercia del flujo, la desaceleración del flujo viscoso por la pared y el gradiente de presión adverso que actúa en la dirección aguas arriba = 0 o < 0.
Si el gradiente de presión es adverso en la localización de la superficie entre las secciones ‘1-4’ (ver Figura 3), la distribución de la velocidad u = u(x,y) en la capa límite cambia gradualmente; volviéndose «menos llena», disminuyendo la inclinación en los chorros de fluido que están más cerca de la pared y poseyendo menos cantidad de energía cinética (ver las formas del perfil de velocidad en la Figura 3) que penetran lejos aguas abajo en la región de presión aumentada. En algunas secciones, por ejemplo la sección ‘4’, las partículas de fluido que se encuentran en la línea de flujo ‘a-a’ (línea punteada en la Figura 3) – habiendo agotado completamente su suministro de energía cinética se desaceleran (ua = 0).
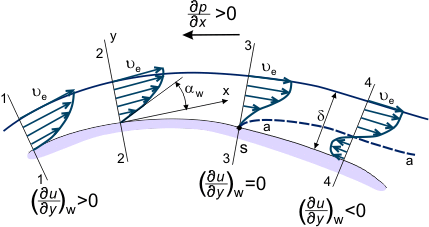
Figura 3. Capa límite en el flujo sobre una superficie cubierta.
La presión estática y el valor del gradiente de presión no varían a través del espesor de la capa límite. Por lo tanto, las partículas de fluido que están más cerca de la pared que la línea ‘a-a’ y que poseen aún menos cantidad de energía, comienzan a moverse en dirección opuesta bajo la influencia del gradiente de presión en la sección ‘4-4’ (ver Figura 3). Así, la relación:
De esta manera, en algunos lugares de la superficie, el perfil de velocidad cambia. Este cambio se caracteriza por la alteración del signo de la derivada w de positivo (sección 2, figura 3) a negativo (sección 4). Por supuesto, también es posible definir la sección en la que w = 0 (sección 3, Figura 3). Esta sección se denomina sección de separación de la capa límite (correspondientemente el punto «S» en la superficie de esta sección es el punto de separación). Se caracteriza por el desarrollo de una zona de flujo inverso: el flujo alrededor del cuerpo ya no es suave, la capa límite se vuelve considerablemente más gruesa y las líneas de flujo externas se desvían de la superficie del cuerpo volado. Aguas abajo del punto de separación, la distribución de la presión estática a lo largo del espesor de la capa no es estable y la distribución de la presión estática a lo largo de la superficie no se corresponde con la distribución de la presión en el flujo externo, no viscoso.
La separación es seguida por el desarrollo de zonas de flujo inverso y remolinos, en los que la energía cinética suministrada por el flujo externo se transforma en calor bajo la influencia de las fuerzas de fricción. La separación del flujo, acompañada de la disipación de energía en las zonas de remolinos de flujo inverso, da lugar a efectos indeseables como el aumento de la resistencia aerodinámica de los vehículos o las pérdidas hidráulicas en los canales.
Por otra parte, los flujos separados se utilizan en diferentes dispositivos para la mezcla intensiva de fluidos (por ejemplo, para mejorar la mezcla de combustible y aire en las cámaras de combustión de los motores). Cuando los fluidos viscosos fluyen en canales con una sección transversal variable (gradiente de presión alternante), la zona de separación puede ser local si la sección del difusor es seguida por la sección del confusor, donde el flujo separado volverá a unirse a la superficie (véase la figura 4a). Cuando el flujo se separa del borde de salida del cuerpo (por ejemplo, del borde de salida del ala), se forma la llamada estela por capas límite «enlazadas» (véase la figura 4b).
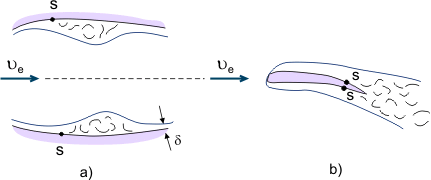
Figura 4. Fenómenos de separación de la capa límite.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. y Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.