El análisis amortizado se utiliza para los algoritmos que tienen operaciones caras que ocurren sólo en raras ocasiones.

El análisis de la complejidad amortizada se utiliza más comúnmente con las estructuras de datos que tienen estado que persiste entre las operaciones.La idea básica es que una operación costosa puede alterar el estado de manera que el peor caso no pueda volver a ocurrir durante mucho tiempo, amortizando así su coste.
Sea T1, T2, …, Tk las complejidades de una secuencia de operaciones sobre una estructura de datos. La complejidad amortizada de una sola operación en esta secuencia es(T1 + T2 + …+ Tk) / k.
Ejemplo: un array dinámico
En un array dinámico, los elementos se almacenan al principio de un array fijo subyacente, y las posiciones restantes no se utilizan.
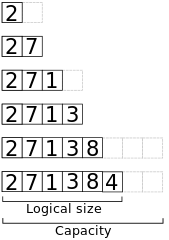
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Aquí se muestra una vista de la memoria al añadir los elementos 2, 7, 1, 3, 8, 4 a un array inicialmente vacío con capacidad 2.
Tiempo en el peor de los casos
La complejidad del tiempo en el peor de los casos para añadir un elemento a una matriz de longitud n, utilizando este algoritmo, es Θ(n).Si la matriz está llena, el algoritmo asigna una nueva matriz de longitud 2n, y luego copia los elementos de la antigua matriz en la nueva.
Cuidado, este resultado es demasiado pesimista.Las siguientes n operaciones de anexión serán mucho más baratas -cada una de ellas se ejecutará en tiempo constante, ya que la matriz recién asignada tiene espacio para todos los nuevos elementos.
Tiempo amortizado
Un análisis del tiempo amortizado permite comprender mucho mejor el algoritmo.
Consideremos una secuencia de n operaciones de anexión, en la que empezamos con una matriz de longitud 1. Un análisis cuidadoso muestra que el tiempo total de estas operaciones es sólo Θ(n).
- Habrá un total de n operaciones de asignación e incremento de tiempo constante.
- El redimensionamiento ocurrirá sólo en la operación 1, 2, 4, …, 2k, para un total de 1 + 2 + 4 + …+ 2k = 2-2k – 1 operaciones de copia de elementos de tiempo constante. Dado que 2k ≤ n, esto es a lo sumo 2n – 1.
Por lo tanto, la complejidad del tiempo amortizado para una sola operación de añadir es Θ(1).
Más sobre el análisis del algoritmo

Complejidad del tiempo: Cuenta tus pasos

Notación Big O