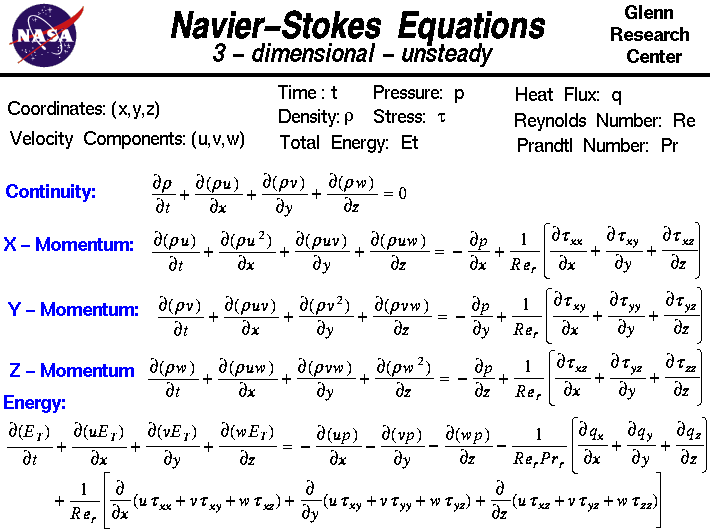
En esta diapositiva se muestra la forma inestable tridimensional de las ecuaciones de Navier-Stokes. Navier, en Francia, a principios de 1800. Las ecuaciones son extensiones de las ecuaciones de Euler e incluyen los efectos de la viscosidad en el flujo. Estas ecuaciones son muy complejas, pero a los estudiantes de ingeniería se les enseña a derivarlas en un proceso muy similar a la derivación que presentamos en la página web de la conservación del momento.
Las ecuaciones son un conjunto de ecuaciones diferenciales acopladas y, en teoría, podrían resolverse para un determinado problema de flujo utilizando métodos de cálculo.Pero, en la práctica, estas ecuaciones son demasiado difíciles de resolver analíticamente.En el pasado, los ingenieros hacían aproximaciones y simplificaciones adicionales al conjunto de ecuaciones hasta que tenían un grupo de ecuaciones que podían resolver.Recientemente, se han utilizado ordenadores de alta velocidad para resolver aproximaciones a las ecuaciones utilizando una variedad de técnicas como diferencias finitas, volúmenes finitos, elementos finitos y métodos espectrales.Esta área de estudio se denomina Dinámica de Fluidos Computacional o CFD.
Las ecuaciones de Navier-Stokes consisten en una ecuación de continuidad dependiente del tiempo para la conservación de la masa, tres ecuaciones de conservación del momento dependientes del tiempo y una ecuación de conservación de la energía dependiente del tiempo.Hay cuatro variables independientes en el problema, las coordenadas espaciales x, y, z de algún dominio, y el tiempo t. Hay seis variables dependientes: la presión p, la densidad r y la temperatura T (que está contenida en la ecuación de energía a través de la energía total Et) y tres componentes del vector velocidad: la componente u está en la dirección x, la componente v está en la dirección y y la componente w está en la dirección z. Todas las variables dependientes son funciones de las cuatro variables independientes.Las ecuaciones diferenciales son, por lo tanto, ecuaciones diferenciales parciales y no las ecuaciones diferenciales ordinarias que se estudian en la clase de cálculo inicial.
Notarás que el símbolo diferencial es diferente al habitual «d /dt» o «d /dx» que ves para las ecuaciones diferenciales ordinarias. El símbolo «
» se utiliza para indicar las derivadas parciales. El símbolo indica que debemos mantener fijas todas las variables independientes, excepto la variable junto al símbolo, cuando se calcula una derivada. El conjunto de ecuaciones son:
Continuidad: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momento: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Momentum: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momentum: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energía: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
donde Re es el número deReynoldsque es un parámetro de similitud que es la relación de la escala de lainercia del flujo con las fuerzas viscosas en el flujo. Las variables q son los componentes del flujo de calor y Pr es el número de Prandtl, un parámetro de similitud que es la relación entre las tensiones viscosas y las térmicas. Nuestro vector de velocidad tiene tres componentes; el tensor de tensiones tiene nueve componentes. Cada componente del tensor de tensiones es a su vez una segunda derivada de las componentes de la velocidad.
Los términos del lado izquierdo de las ecuaciones de momento se denominan términos de convección de las ecuaciones.La convección es un proceso físico que ocurre en un flujo de gas en el que alguna propiedad es transportada por el movimiento ordenado del flujo.Los términos del lado derecho de las ecuaciones de momento que se multiplican por el número de Reynolds inverso se denominan términos de difusión.La difusión es un proceso físico que ocurre en un flujo de gas en el que alguna propiedad es transportada por el movimiento aleatorio de las moléculas del gas.La difusión está relacionada con el tensor de esfuerzo y con la viscosidad del gas. La turbulencia, y la generación de capas límite, son el resultado de la difusión en el flujo. Las ecuaciones de Euler sólo contienen los términos de convección de las ecuaciones de Navier-Stokes y, por tanto, no pueden modelar las capas límite. Hay una simplificación especial de las ecuaciones de Navier-Stokes que describen los flujos de la capa límite.
Nótese que todas las variables dependientes aparecen en cada ecuación.Para resolver un problema de flujo, hay que resolver las cinco ecuaciones simultáneamente; por eso llamamos a esto un sistema de ecuaciones acoplado.En realidad hay algunas otras ecuaciones que se requieren para resolver este sistema. Sólo mostramos cinco ecuaciones para seis incógnitas. Una ecuación de estado relaciona la presión, la temperatura y la densidad del gas.Y necesitamos especificar todos los términos del tensor de tensiones.En CFD los términos del tensor de tensiones son a menudo aproximados por un modelo de turbulencia.
Actividades:
Visitas guiadas
Navegación ..
Guía para principiantes Página principal