Sun, 18 Jun 2006
1+1=2
Los Principia Mathematica de Whitehead y Russell son famosos por dedicar mil páginas a demostrar que 1+1=2. Por supuesto, también demuestra muchas otras cosas. Si hubieran querido demostrar sólo que 1+1=2, probablemente habría ocupado sólo la mitad de espacio.
Principia Mathematica es un libro extraño, que merece la pena estudiar desde un punto de vista histórico y también matemático. Fue escrito en torno a 1910, y la lógica matemática estaba aún en sus inicios, recién salida de la transformación realizada por Peano y Frege. La notación es algo oscura, porque la notación matemática ha evolucionado mucho desde entonces. Al igual que un programa de ordenador mal escrito, gran parte del volumen de Principia Mathematica es código repetido, secciones separadas que dicen esencialmente las mismas cosas, porque los autores aún no han aprendido las técnicas que permitirían combinar estas secciones en una sola.
Por ejemplo, la sección ∗22, «Cálculo de clases», comienza definiendo la relación de subconjunto (∗22.01), y las operaciones de unión e intersección de conjuntos (∗22.02 y .03), el complemento de un conjunto (∗22.04), y la diferencia de dos conjuntos (∗22.05). A continuación, demuestra la conmutatividad y la asociatividad de la unión de conjuntos y de la intersección de conjuntos (∗22.51, .52, .57 y .7), varias propiedades como ¡¡¡alpha\cap\alpha = \alpha!! (∗22.5) y otras similares, hasta llegar a teoremas como ∗22.92: ¡¡¡¡Subconjunto de beta!!! ¡¡¡Flecha derecha!!! ¡¡¡¡Captura de beta-alfa!!!
La sección ∗23 es «Cálculo de relaciones» y comienza casi exactamente igual, definiendo la relación de subrelación (∗23.01), y las operaciones de unión e intersección de relaciones (∗23.02 y .03), el complemento de una relación (∗23.04) y la diferencia de dos relaciones (∗23.05). Más adelante demuestra la conmutatividad y la asociatividad de la unión y la intersección de relaciones (∗23.51, .52, .57 y .7), varias propiedades como ¡¡¡alpha\dot\cap\alpha = \alpha!! (∗22.5) y otras similares, hasta llegar a teoremas como ∗23.92: ¡¡¡Subconjunto de beta!!! ¡¡Flecha derecha!! ¡¡¡Subconjunto de beta!!! ¡¡¡Cupón de beta!!! ¡¡¡¡Alfa!!!
La sección ∗24 trata de la existencia de conjuntos, el conjunto nulo ¡¡Lambda!!, el conjunto universal ¡¡¡¡V!!!y sus propiedades, etc., y luego la sección ∗24 se duplica en ∗25 en una serie de teoremas sobre la existencia de relaciones, la relación nula !!!\NLambda!!, la relación universal !!!\Nde V!!, sus propiedades, etc.
Así lo hicieron Whitehead y Russell en 1910. ¿Cómo lo haríamos hoy en día? Una relación entre S y T se define como un subconjunto deS × T y, por tanto, es un conjunto. La unión, la intersección, la diferencia y las demás operaciones son precisamente las mismas para las relaciones que para los conjuntos, porque las relaciones son conjuntos. Todos los teoremas sobre uniones e intersecciones de relaciones, como el de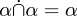 
, desaparecen, porque ya los hemos demostrado para los conjuntos y las relaciones son conjuntos. La relación nula es el conjunto nulo. La relación universal es el conjunto universal.
Una gran cantidad de otra maquinaria desaparece en 2006, debido a la unificación de relaciones y conjuntos. Principia Mathematica necesita una notación especial y una definición especial para el resultado de restringir una relación a aquellos pares cuyo primer elemento es un miembro de un conjunto particular S, o cuyo segundo elemento es un miembro de S, o ambos elementos son miembros de S; en 2006 simplemente usaríamos la operación ordinaria de intersección de conjuntos y hablaríamos de R ∩(S×B) o lo que sea.
Whitehead y Russell no pudieron hacer esto en 1910 porque faltaba una pieza crucial de la maquinaria: el par ordenado. En 1910 nadie sabía cómo construir un par ordenado a partir de la lógica y los conjuntos. En 2006 (o incluso en 1956), definiríamos el par ordenado <a, b> como el conjunto {{a}, {a, b}}. Luego demostraríamos como un ateorema que <a, b> = <c, d> si y sólo si a=c y b=d, utilizando las propiedades de los conjuntos. Entonces definiríamos A×B como el conjunto de todos los p tales que p = <a,b> ∧ a ∈ A ∧ b∈ B. Entonces definiríamos una relación sobre los conjuntosA y B como un subconjunto de A×B. Entonces obtendríamos todo ∗23 y ∗25 y un montón de ∗33 y ∗35 y ∗36 gratis, y probablemente muchas otras cosas también.
(Por cierto, lo de {{a}, {a, b}} fue inventado por Kuratowski. Se suele atribuir a Norbert Wiener, pero la idea de Wiener, aunque similar, era en realidad más complicada.)
No hay pares ordenados en Principia Mathematica, salvo implícitamente. Apenas hay conjuntos. Whitehead y Russell quieren basar todo en la lógica. Para Whitehead y Russell, la noción fundamental es la «función proposicional», que es una función φ cuya salida es un valor de verdad. Para cada función de este tipo, hay un conjunto correspondiente, que denotan por ¡¡¡que x\phi(x)!!!, el conjunto de todas las xs tales que φ(x) es verdadera. Para Whitehead y Russell, la relación está implicada por una función proposicional de dos variables, de forma análoga a como un conjunto está implicado por una función proposicional de una variable. En 2006, prescindimos de las «funciones de dos variables» y nos limitamos a hablar de funciones cuyo (único) argumento es un par ordenado; una relación se convierte entonces en el conjunto de todos los pares ordenados para los que una función es verdadera.
Se supone que Russell dijo que el descubrimiento del trazo de Sheffers (un único operador lógico a partir del cual se pueden construir todos los demás operadores lógicos) era un avance tremendo, y que lo cambiaría todo. Esto nos parece extraño ahora, porque el descubrimiento del trazo de Sheffer parece tan simple, y realmente no cambia nada importante. Basta con añadir una nota al principio del capítulo 1 que diga que ∼p y p∨q son abreviaturas de p|p yp|p.|.q|q, respectivamente, demostrar los cinco axiomas fundamentales, y dejar todo lo demás igual. Pero Russell podría haber dicho con cierta justicia lo mismo sobre el descubrimiento de que los pares ordenados pueden ser interpretados como conjuntos, un simple descubrimiento que realmente habría transformado los Principia Mathematicain en una obra bastante diferente.
De todos modos, con estos antecedentes, podemos discutir la prueba de 1+1=2 de los Principia Mathematica. Esto ocurre bastante tarde en Principia Mathematica, en la sección ∗102. Mi versión abreviada sólo llega hasta ∗56, pero es suficiente para llegar al importante teorema precursor, ∗54.43, escaneado a continuación:
La notación puede ser abrumadora, así que vamos a centrarnos sólo en el enunciado del teorema, ignorando todo lo demás, incluso el útil comentario de la parte inferior:
Este es el teorema que se demuestra; lo que sigue es la prueba.
Ahora debo explicar la notación, que ha cambiado algo desde 1910. En primer lugar, Principia Mathematica utiliza la notación de «puntos» de Peano para desambiguar la precedencia, mientras que ahora utilizamos paréntesis. La notación de puntos requiere cierto tiempo de adaptación, pero tiene algunas ventajas claras sobre los paréntesis. La idea es que se indica la agrupación poniendo puntos, de modo que (1+2)×(3+4)&veces(5+6) se escribe como1+2.×.3+4.×.5+6. La subfórmula del medio está entre un par de puntos. La subfórmula (1+2) también está entre un par de puntos, pero el punto del extremo izquierdo es superfluo y lo omitimos; del mismo modo, la subfórmula (5+6) está delimitada por un punto a la izquierda y por el final de la fórmula a la derecha.
¿Y si necesitas anidar paréntesis? Entonces se utilizan más puntos. Un punto doble (:) es como un punto simple, pero más fuerte. Por ejemplo, escribimos ((1+2)×3)+4 como 1+2 . × 3 : + 4, y el punto doble aísla toda la expresión 1+2 . × 3 en una única subfórmula a la que se aplica el +4.
A veces se necesitan más niveles de precedencia, y entonces se utilizan puntos triples (.: y :.) y cuádruples (::). Esta fórmula, como ves, tiene puntos dobles y triples. Si traducimos los puntos a la notación estándar de paréntesis, tenemos \vdash ((\alpha, \beta \en 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \en 2)))$$. Esto tiene un aspecto bastante más desordenado que la versión con los puntos, y las fórmulas incomplicadas pueden tener problemas para averiguar qué paréntesis coinciden con cuál. Con los puntos, siempre es fácil. Así que creo que es un poco desafortunado que esta convención haya caído en desuso.
El símbolo ¡¡¡dash!!! no ha cambiado; significa que la fórmula a la que se aplica se afirma como verdadera. ¡¡¡¡Supset!!! es implicación lógica, y ¡¡¡equiv!! es equivalencia lógica. Λ es el conjunto vacío, que hoy escribimos como ∅. ∩ ∪ y ∈ tienen sus significados modernos: ∩ y ∪ son los operadores de intersección de conjuntos y de unión, y x∈y significa que x es un elemento del conjunto y.
Los puntos restantes son semánticos. α y β son conjuntos. 1denota el conjunto de todos los conjuntos que tienen exactamente un elemento. Es decir, es el conjunto { c : existe a tal que c = {a } }. Los teoremas sobre 1 incluyen, por ejemplo:
- que Λ∉1 (∗52.21),
- que si α∈1 entonces existe algún x tal que α ={x} (∗52.1), y
- que {x}∈1 (∗52.22).
2 es igualmente el conjunto de todos los conjuntos que tienen exactamente dos elementos. Un teorema importante sobre 2 es ∗54.3, que dice que $$\ast54.3. \vdash 2 = \hat\alpha\{ (\existe x) \> .\>x\in\alpha \> . \> \alpha – \iota`x\in 1 \}.$$En la notación de Principia Mathematica, {x}, el conjunto que contiene x y nada más, se escribe ι’x, por lo que este teorema dice que 2 es idéntico al conjunto de todos los α tales queα tiene algún elemento x , que, cuando se elimina de α, deja un conjunto de 1 elemento.
Así que aquí está el teorema ∗54.43 de nuevo:
Afirma que si los conjuntos α y β tienen cada uno exactamente un elemento, entonces son disjuntos (es decir, no tienen elementos en común) si y sólo si su unión tiene exactamente dos elementos.
La demostración, que aparece en la exploración anterior tras la palabra «Dem.» (abreviatura de «demostración») dice así:
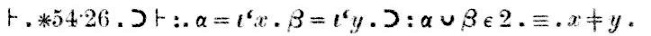
«El teorema ∗54.26implica que si α = {x} y β = {y}, entoncesα∪β tiene 2 elementos si y sólo si x esdiferente de y.»
«Por el teorema ∗51.231, esta última parte (x es diferente dey) es cierta si y sólo si {x} y {y} sondisjuntos.»
«Por ∗13.12, este último bit ({x} y {y} son disjuntos) es verdadero si y sólo si α y β mismos son disjuntos.» La conclusión parcial en este punto, que se etiqueta como (1), es que si α = {x} y β ={y}, entonces α∪β ∈ 2 si y sólo siα∩β = Λ.
La prueba continúa: «La conclusión (1), con los teoremas ∗11.11 y ∗11.35,implica que si existen x e y de modo que α es{x} y β es {y}, entonces α∪β ∈ 2 si y sólo si α y β son disjuntos». Esta conclusión está etiquetada como (2).
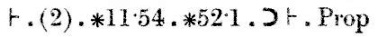
Por último, la conclusión (2), junto con los teoremas ∗11.54 y ∗52.1,implica el teorema que intentábamos demostrar.
Quizá lo que hay que notar aquí es lo pequeños que son los pasos.∗54.26, del que depende mucho este teorema, es casi lo mismo; afirma que {x}∪{y} ∈ 2 si y sólo si x≠y. ∗54.26, a su vez, depende de ∗54.101, que diceque α tiene 2 elementos si y sólo si existen x ey, no iguales, tales que α = {x} ∪{y}. El teorema ∗54.101 es sólo un poco diferente de la definición de 2. El teorema ∗51.231 dice que {x} y {y} son disjuntos si y sólo si x e y son diferentes.∗52.1 es una propiedad básica de 1; ya lo vimos antes.
Los otros teoremas citados en la demostración son cuestiones técnicas muy pequeñas. ∗11.54 dice que se puede tomar una afirmación de que dos cosas existen y separarla en dos afirmaciones, cada una de las cuales afirma que una de las cosas existe. ∗11.11 es aún más delgado: dice que si φ(x, y) es siempre verdadera, entonces se puede adjuntar un cuantificador universal, y afirmar que φ(x, y) es verdadera para todo x e y. El artículo ∗13.12 se refiere a la sustitución de iguales por iguales: si x e y son iguales, entonces x posee una propiedad ψ si y sólo si y también la posee.
No he visto las últimas partes de Principia Mathematica, porque mi copia se detiene después de la sección ∗56, y el material aritmético es muy posterior. Pero este teorema tiene claramente el sentido de 1+1=2, y el teorema posterior (∗110.643) que afirma realmente 1+1=2 depende en gran medida de éste.
Aunque no estoy completamente seguro de lo que va a pasar después (ya he perdido demasiado tiempo en esto como para dedicar más tiempo a conseguir la versión completa de la biblioteca) puedo hacer una conjetura. Principia Mathematica va a definir el número 17 como el conjunto de todos los conjuntos de 17 elementos, y de forma similar para cualquier otro número; el uso del símbolo 2 para representar el conjunto de todos los conjuntos de 2 elementos lo prefigura. Los conjuntos de todos los conjuntos de un tamaño determinado se identificarán entonces como los «números cardinales».
Los Principia Mathematica definirán la suma de los números cardinales p y q de la siguiente manera: tomar un conjunto representativo a de p;a tiene p elementos. Tomemos un conjunto representativo bde q; b tiene q elementos. Sea c =a∪b. Si c es un miembro de algún número cardinal r, y si a y b son disjuntos, entonces la suma de p y q es r.
Con esta definición, se pueden demostrar las propiedades deseables habituales de la adición, como x + 0 = x, x + y = y + x, y 1 + 1 = 2.
En particular, 1+1=2 se deduce directamente del teorema ∗54.43; es justo lo que queremos, porque para calcular 1+1, debemos encontrar dos representantes disjuntos de 1, y tomar su unión; ∗54.43 afirma que la unión debe ser un elemento de 2, independientemente de los representantes que elijamos, de modo que 1+1=2.
Post scriptum: Peter Norvig dice que el circunflejo en la notación de Principia Mathematica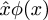 
es la fuente última del uso de la palabralambda para denotar una función anónima en los lenguajes de programación Lisp y Python. Estoy seguro de que sabes que estos lenguajes obtienen «lambda» del uso de la letra griega λ por parte de Alonzo Church para representar la abstracción de funciones en su «λ-calculus»: En Lisp,(lambda (u) B) es una función que toma un argumentou y devuelve el valor de B; en el λ-calculo, λu.B es una función que toma un argumentou y devuelve el valor de B. Norvig dice que Church planeaba originalmente escribir la funciónλu.B como û.B, pero su impresora no podía hacer acentos circunflejos. Así que pensó en mover el circunflejo a la izquierda y usar una lambda mayúscula en su lugar:Λu.B. La mayúscula Λ se parecía demasiado a lo lógico y ∧, lo que resultaba confuso, así que usó lambdaλ en minúscula en su lugar.
Post scriptum: Todo el mundo dice siempre «Russell y Whitehead».Los resultados de Google para «Russell y Whitehead» superan en número a los de «Whitehead y Russell» por dos a uno, por ejemplo. ¿Por qué? La portada y la página del título dicen «Alfred North Whitehead y Bertrand Russell, F.R.S.». ¿Cómo y cuándo perdió Whitehead el primer puesto?
enlace permanente