- Objetivos de aprendizaje
- Mallas
- Ejemplo 1
- Ejemplo 2
- Revisa los ejercicios
- Respuestas
- Prismas
- Área de la superficie de un prisma usando redes
- Ejemplo 3
- Ejercicios de repaso
- Respuestas
- Cilindros
- Área de la superficie de un cilindro usando redes
- Ejemplo 4
- Área de la superficie de un cilindro usando una fórmula
- Ejemplo 5
- Ejemplo 6
- Ejemplo 7
- Esferas
- Área superficial de una esfera
- Ejemplo 8
- Ejemplo 9
- Ejercicios de repaso
- Respuestas
Objetivos de aprendizaje
- Entender las redes.
- Utilizar las redes para representar prismas.
- Hallar el área de la superficie de un prisma.
- Hallar el área de la superficie de los cilindros.
- Hallar el área de la superficie de una esfera.
Mallas
Una última forma de representar un sólido es utilizar una red. Si se recorta una red, se puede doblar en un modelo de una figura. Las redes también se pueden utilizar para analizar un solo sólido. Aquí hay un ejemplo de una red para un cubo.
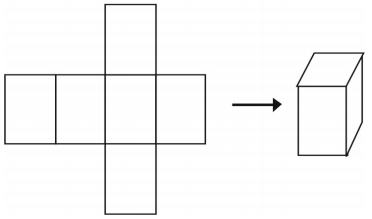
Hay más de una manera de hacer una red para una sola figura.
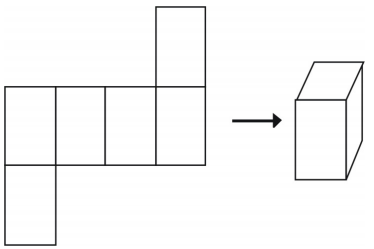
Sin embargo, no todos los arreglos crearán un cubo.
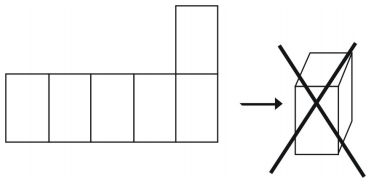
Ejemplo 1
¿Qué tipo de figura crea la red? Dibuja la figura.
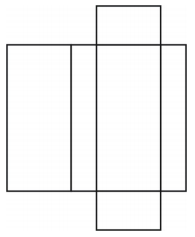
La red crea un prisma rectangular en forma de caja como se muestra a continuación.
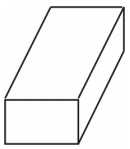
Ejemplo 2
¿Qué tipo de red puedes dibujar para representar la figura mostrada? Dibuja la red.
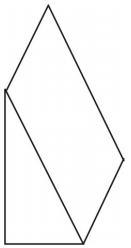
Se muestra una red para el prisma. Son posibles otras redes.
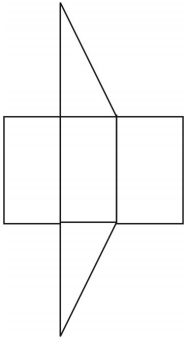
Revisa los ejercicios
Dibuja una red para cada uno de los siguientes:
Respuestas
Prismas
Un prisma es una figura tridimensional con un par de extremos paralelos y congruentes, o bases. Las caras de un prisma son paralelogramos. Los prismas se identifican por sus bases.
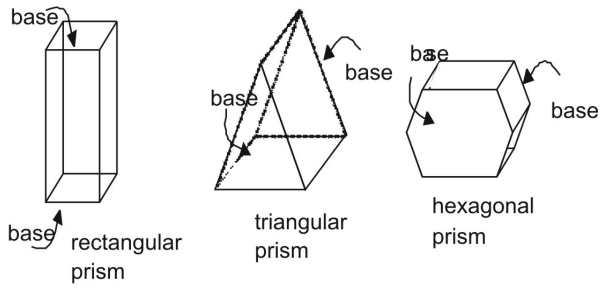
Área de la superficie de un prisma usando redes
Los prismas anteriores son prismas rectos. En un prisma recto, las caras laterales son perpendiculares a las bases del prisma. Compara un prisma recto con un prisma oblicuo, en el que las caras y las bases no son perpendiculares.
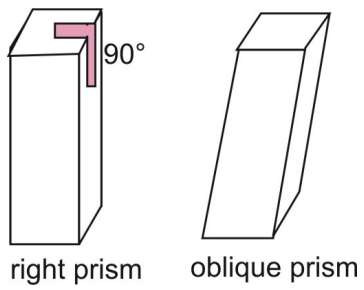
Dos postulados que se aplican al área son el postulado de congruencia del área y el postulado de adición del área.
Puedes utilizar una red y el postulado de adición de áreas para encontrar el área de la superficie de un prisma recto.
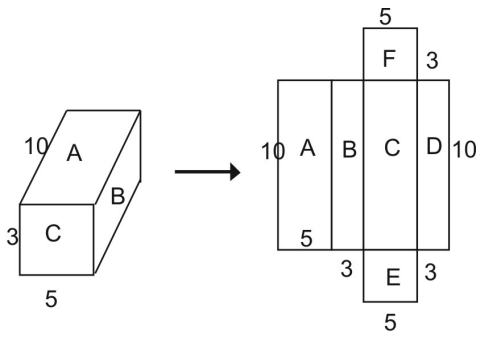
A partir de la red, puedes ver que el área de la superficie de todo el prisma es igual a la suma de las figuras que componen la red:
Superficie total = área A + área B + área C + área D + área E + área F
Usando la fórmula del área de un rectángulo, puedes ver que el área del rectángulo A es:
A = l – w
A = 10 – 5 = 50 unidades cuadradas
De forma similar, las áreas de los otros rectángulos se vuelven a insertar en la ecuación anterior.
Superficie total = área A + área B + área C + área D + área E + área F
Superficie total = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3)
Superficie total = 50 + 30 + 50 + 30 + 15 + 15
Superficie total = 190 unidades cuadradas
Ejemplo 3
Usa una red para hallar la superficie del prisma.
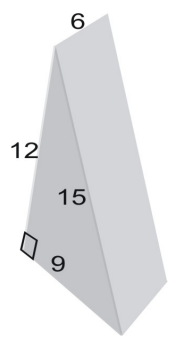
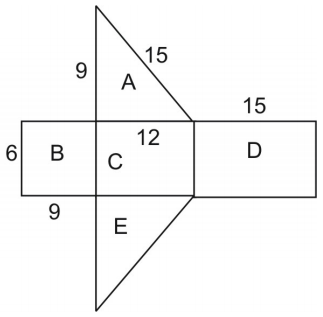
El área de la red es igual al área de la superficie de la figura. Para hallar el área del triángulo, utilizamos la fórmula:
\Ndice A=\Nfrac{1}{2}hb\Ndonde h es la altura del triángulo y b es su base.
Nota que los triángulos A y E son congruentes por lo que podemos multiplicar el área del triángulo A por 2.
estilo de visualización del texto {área}=texto {área}A+texto {área}B+texto {área}C+texto {área}D+texto {área}E
estilo de visualización del texto {área}=2(texto {área}A)+texto {área}B+texto {área}E. }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\
Thus, la superficie es de 324 unidades cuadradas.
Ejercicios de repaso
Para cada uno de los siguientes encuentra la superficie son a utilizando el método de las redes y el perímetro


- La base de un prisma es un triángulo rectángulo cuyos catetos son 3 y 4 y muestran una altura de 20. ¿Cuál es el área total del prisma?
- Un prisma hexagonal recto mide 24 pulgadas y tiene bases que son hexágonos regulares que miden 8 pulgadas de lado. ¿Cuál es el área total de la superficie?
- ¿Cuál es el volumen del prisma en el problema #4?
En las siguientes preguntas, un granero tiene forma de prisma pentagonal con dimensiones mostradas en pies:

- ¿Cuántos pies cuadrados (excluyendo el techo) hay en la superficie del granero que se va a pintar?
- Si un galón de pintura cubre 250 pies cuadrados, ¿cuántos galones de pintura se necesitan para pintar el granero?
- Una caja de cartón es un cubo perfecto con una arista que mide 17 pulgadas. ¿Cuántos pies cúbicos puede contener?
- Una piscina tiene 16 pies de ancho, 32 pies de largo y una profundidad uniforme de 4 pies. ¿Cuántos pies cúbicos de agua puede contener?
- Una caja de cereales tiene 25 cm de largo, 9 cm de ancho y 30 cm de alto. ¿Cuántos cereales puede contener?
Respuestas
Mallas y perímetro:
- 40,5 pulg2
- 838 cm2
- 252 unidades cuadradas
- 1484.6 unidades cuadradas
- 3990,7 pulgadas cúbicas
El granero:
- 2450 pies cuadrados
- 10 galones de pintura
- 2,85 pies cúbicos (ten cuidado aquí. Las unidades en el problema se dan en pulgadas pero la pregunta pide pies.)
- 2048 pies cúbicos
- 6750 cm3
Cilindros
Un cilindro es una figura tridimensional con un par de extremos circulares paralelos y congruentes, o bases. Un cilindro tiene un solo lado curvo que forma un rectángulo cuando se coloca en posición plana.
Al igual que los prismas, los cilindros pueden ser rectos u oblicuos. El lado de un cilindro recto es perpendicular a sus bases circulares. El lado de un cilindro oblicuo no es perpendicular a sus bases.
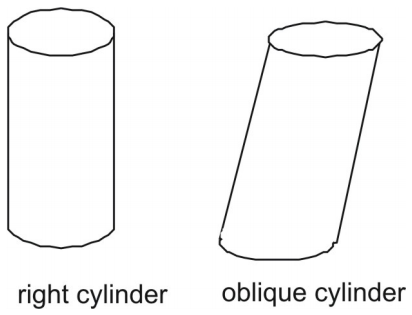
Área de la superficie de un cilindro usando redes
Se puede deconstruir un cilindro en una red.
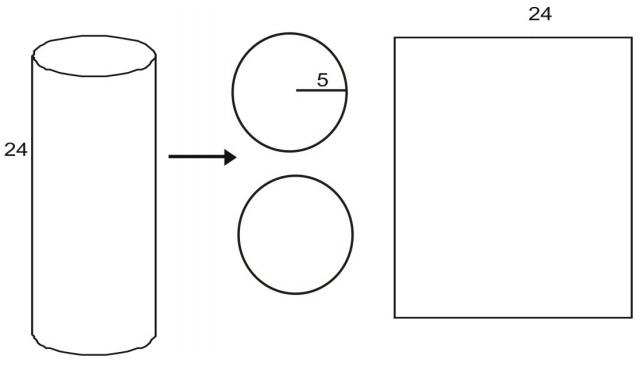
El área de cada base viene dada por el área de un círculo:
A=\pi{r}^2\
A=\pi(5)^2\
A=25\pi\
A\aprox(25)(3,14)=78,5\
El área del área lateral rectangular L viene dada por el producto de un ancho y un alto. La altura viene dada por 24. Puedes ver que la anchura del área es igual a la circunferencia de la base circular.
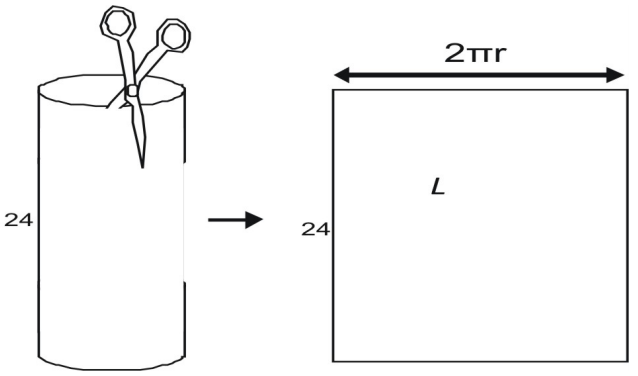
Para encontrar la anchura, imagina que desmontas un cilindro en forma de lata con unas tijeras. Al cortar el área lateral, ves que es igual a la circunferencia de la parte superior de la lata. La circunferencia de un círculo viene dada por C = 2πr, el área lateral, L, es
L=2{pi}rh\\
L=2{pi}(5)(24)\\N-
L=240{pi}
L\Naprox(240)(3.14)=753,6\
Ahora podemos hallar el área de todo el cilindro utilizando A = (área de las dos bases) + (área del lado lateral).
A=2(75,36)+753,6\
A=904,32\
Puedes ver que la fórmula que hemos utilizado para hallar el área total de la superficie se puede utilizar para cualquier cilindro recto.
Ejemplo 4
Usa una red para encontrar el área de la superficie del cilindro.
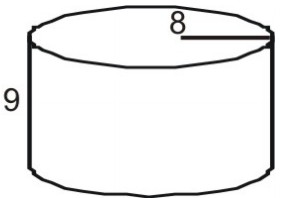
Primero dibuja y rotula una red para la figura.
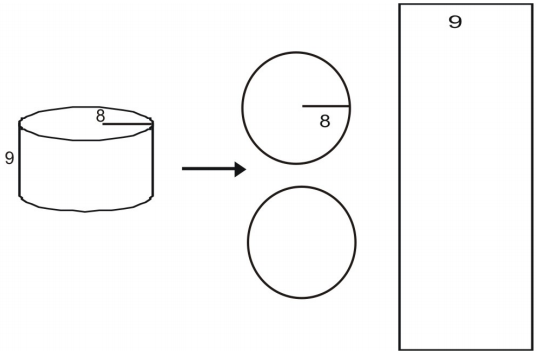
Calcula el área de cada base.
A=pi{r}^2\
A=pi(8)^2\\
A=64\\pi{
A\\Naprox(64)(3.14)=200.96\\
Calculate L.
L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452,16\
Encuentra el área de todo el cilindro.
A=2(200,96)+452,16\
A=854.08\\N
Así, el área total de la superficie es de aproximadamente 854,08 unidades cuadradas
Área de la superficie de un cilindro usando una fórmula
Has visto cómo usar las redes para encontrar el área total de la superficie de un cilindro. El postulado se puede desglosar para crear una fórmula general para todos los cilindros rectos.
A = 2B + L

Nota que la base, B, de cualquier cilindro es: B = πr2
El área lateral, L, para cualquier cilindro es:
L={ancho del área lateral}\cdot\text{altura del cilindro}\
L={circunferencia de la base}\cdot\text{altura del cilindro}\
L=2\pi{r}\cdot{h}\7676>
Juntando las dos ecuaciones obtenemos:
Al calcular a a partir de la ecuación se obtiene:
La superficie de un cilindro recto: Un cilindro recto de radio r y altura h puede expresarse como:
A = 2πr2 + 2πrh
o:
A = 2πr(r + h)
Puedes utilizar las fórmulas para encontrar el área de cualquier cilindro recto.
Ejemplo 5
Usa la fórmula para hallar el área de la superficie del cilindro.
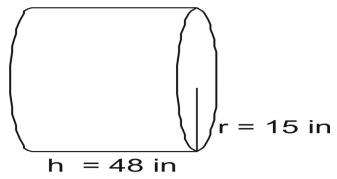
Escribe la fórmula y sustituye los valores y resuelve.
A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\text{ pulgadas cuadradas}\
Ejemplo 6
Halla la superficie del cilindro.
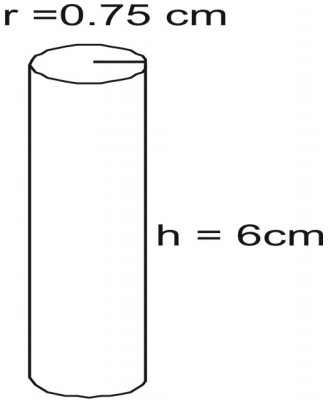
Escribe la fórmula y sustituye los valores y resuelve.
A=2\pi{r}(r+h)\\️A=2(3,14)(0,75)\️A=31.7925\text{ pulgadas cuadradas}\
Ejemplo 7
Hallar la altura de un cilindro que tiene radio 4cm y superficie de 226,08 cm2.
Escribir la fórmula con la información dada y resolver para h.
A=2\pi{r}(r+h)\
226,08=2(3,14)(4)\
226,08=25,12\
226,08=100,48+25,12h\
5=h\
Esferas
Una esfera es una figura tridimensional que tiene forma de bola.

Las esferas pueden caracterizarse de tres maneras.
- Una esfera es el conjunto de todos los puntos que se encuentran a una distancia fija r de un único punto central O.
- Una esfera es la superficie que resulta cuando se gira un círculo alrededor de cualquiera de sus diámetros.
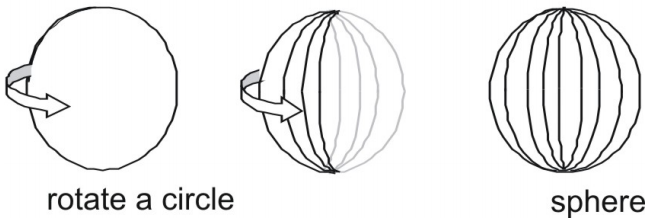
Área superficial de una esfera
Se puede inferir la fórmula del área superficial de una esfera tomando medidas de esferas y cilindros. Aquí mostramos una esfera con un radio de 3 y un cilindro recto con radio y altura de 3 y expresamos el área en términos de π.
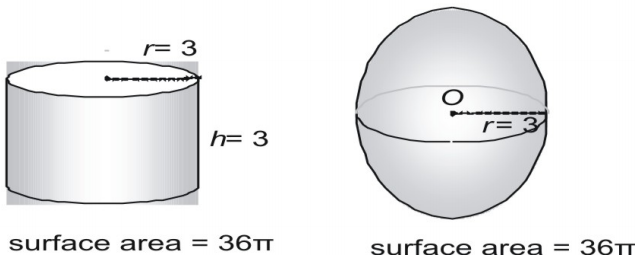
Ahora prueba con un par más grande, expresando el área de la superficie en forma decimal.
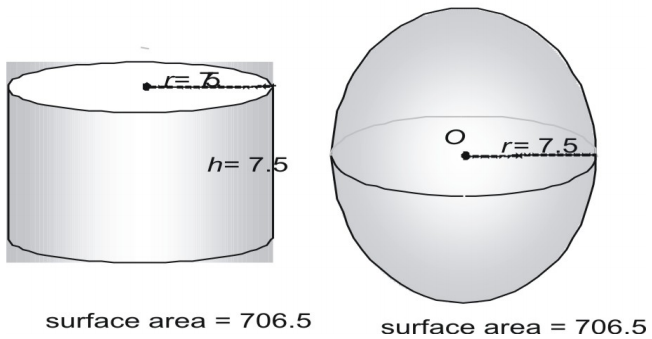
Mira un tercer par.
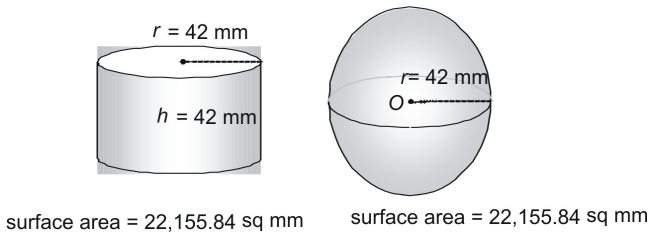
¿Es una coincidencia que una esfera y un cilindro cuyo radio y altura son iguales al radio de la esfera tengan exactamente la misma superficie? En absoluto. De hecho, los antiguos griegos utilizaron un método que demostró que la siguiente fórmula se puede utilizar para encontrar el área de la superficie de cualquier esfera (o cualquier cilindro en el que ).
Ejemplo 8
Hallar el área de la superficie de una esfera con un radio de 14 pies.
Utilizar la fórmula.
A=4\pi{r}^2\
A=4\pi(14)^2\
A=4\pi(196)\
A=784\pi\
2461.76\text{ pies cuadrados usando }3,14\text{ para }\pi\
Ejemplo 9
Hallar la superficie de la siguiente figura en términos de π.
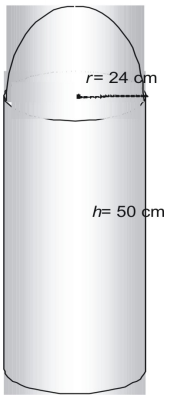
La figura está formada por una media esfera o semiesfera, y un cilindro sin su parte superior.
A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half esfera})=2\pi(576)\\N-(3543>A(\text{media esfera})=1152\pi\text{cm cuadrado}\
Hallar ahora el área del cilindro sin su parte superior.
A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\
Thus, la superficie total es 1152\pi+2976\pi=4128\pi\
Ejercicios de repaso
- Hallar el radio de la esfera que tiene un volumen de 335 cm3.
- Determina la superficie y el volumen de esta forma:

- El radio de una esfera es 4. Halla su volumen y su superficie total.
- Una esfera tiene un radio de 5. Un cilindro recto, que tiene el mismo radio tiene el mismo volumen. Halla la altura y la superficie total del cilindro.
- Esfera: volumen = 296 cm3. Halla el Diámetro.
- Esfera: el área de la superficie es de 179 pulg2. Halla el Radio.
- Las pelotas de tenis con un diámetro de 3,5 pulgadas se venden en latas de tres. La lata es un cilindro. Supongamos que las pelotas tocan la lata por los lados, por arriba y por abajo. ¿Cuál es el volumen del espacio no ocupado por las pelotas de tenis?
- Una esfera tiene una superficie de 36π pulg2. Encuentra su volumen.
- Una cuchara gigante, manejada por una grúa, tiene forma de semiesfera de radio = 21 pulgadas. La cuchara está llena de acero caliente fundido. Cuando el acero se vierte en un tanque de almacenamiento cilíndrico que tiene un radio de 28 pulgadas, el acero fundido se elevará hasta una altura de ¿cuántas pulgadas?
Respuestas
Nótese que estos problemas utilizan π no 3,14.
- 1. Radio = 4,31 cm
- Superficie = 706,86 cm2
Volumen = 1767,15 cm3 - Volumen = 268,08 unidades3
Superficie = 201,06 unidades2 - Altura = 20/3 unidades superficie total = 366,52 unidades2
- Diámetro = 8,27cm
- Radio = 3.77 pulgadas
- Volumen del cilindro = 32,16π pulg3 volumen de las pelotas de tenis = 21,44π pulg3
Volumen del espacio no ocupado por las pelotas de tenis = 33,68 pulg3 - Volumen = 113,10 pulg3
- La altura del acero fundido en el cilindro será de 7,88 pulgadas
.



