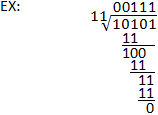Käytä seuraavia laskimia kahden binääriarvon yhteen-, vähennys-, kerto- tai jakolaskun suorittamiseen sekä binääriarvojen muuntamiseen desimaaliarvoihin ja päinvastoin.

Binary Calculation-Add, Subtract, Multiply, or Divide
Muunna binääriarvo desimaaliarvoksi
Muunna desimaaliarvo binääriarvoksi
Aiheeseen liittyvä Heksalaskin | IP-aliverkkolaskin
Binäärijärjestelmä on numeerinen laskentajärjestelmä, joka toimii käytännöllisesti katsoen identtisesti desimaalilukujärjestelmään nähden, joka lienee ihmisille tutumpi. Kun desimaalilukujärjestelmässä käytetään peruslukuna lukua 10, binäärijärjestelmässä käytetään lukua 2. Lisäksi vaikka desimaalijärjestelmässä käytetään numeroita 0-9, binäärijärjestelmässä käytetään vain 0 ja 1, ja kutakin numeroa kutsutaan bitiksi. Näitä eroja lukuun ottamatta laskutoimitukset, kuten yhteen- ja vähennyslasku, kertolasku ja jakolasku, tehdään samojen sääntöjen mukaan kuin desimaalijärjestelmässä.
Lähes kaikki nykyaikainen teknologia ja tietokoneet käyttävät binäärijärjestelmää, koska se on helppo toteuttaa digitaalisissa piireissä logiikkaporttien avulla. On paljon yksinkertaisempaa suunnitella laitteisto, jonka on tunnistettava vain kaksi tilaa, päällä ja pois päältä (tai tosi/väärä, läsnä/poissa jne.). Desimaalijärjestelmän käyttäminen edellyttäisi laitteistoa, joka pystyy havaitsemaan 10 tilaa numeroita 0-9 varten, ja se on monimutkaisempi.
Alla on joitakin tyypillisiä muunnoksia binääri- ja desimaaliarvojen välillä:
Binary/Decimal Conversion
| Decimal | Binary | |
| 0 | 0 | 0 |
| 1 | 1 | |
| 2 | 10 | |
| 3 | 11 | |
| 4 | 100 | |
| 7 | 111 | |
| 8 | 1000 | |
| 10 | 1010 | |
| 16 | 10000 | |
| 20 | 10100 |
Kun työskentely binäärilukujen kanssa voi aluksi tuntua sekavalta, sen ymmärtäminen, että jokainen binäärinen paikka-arvo edustaa 2n:tä, aivan kuten jokainen desimaalipaikka edustaa 10n:tä, auttaa selventämään asiaa. Otetaan esimerkiksi luku 8. Desimaalilukujärjestelmässä 8 sijaitsee ensimmäisessä desimaalipisteen vasemmalla puolella olevassa desimaalipisteessä, joka tarkoittaa 100-paikkaa. Pohjimmiltaan tämä tarkoittaa:
8 × 100 = 8 × 1 = 8
Vertailemalla lukua 18:
(1 × 101) + (8 × 100) = 10 + 8 = 18
Binääriluvussa 8 on 1000. Oikealta vasemmalle luettuna ensimmäinen 0 edustaa 20, toinen 21, kolmas 22 ja neljäs 23; aivan kuten desimaalijärjestelmässä, paitsi että sen perusta on 2 eikä 10. Koska 23 = 8, sen paikalle kirjoitetaan 1, jolloin tulokseksi saadaan 1000. Esimerkkinä 18 eli 10010:
18 = 16 + 2 = 24 + 21
10010 = (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (0 × 20) = 18
Vaiheittainen prosessi muunnettaessa desimaalijärjestelmästä binäärijärjestelmään on seuraava:
- Etsitään suurin 2:n potenssi, joka on annetun luvun sisällä
- Vähennetään tämä arvo annetusta luvusta
- Etsitään suurin 2:n potenssi vaiheessa 2 löydetystä jäännöksestä
- Toistetaan, kunnes jäännös loppuu
- Kirjoitetaan 1 jokaiselle löydetylle binääripaikka-arvolle, ja 0 lopuille
Alla on toinen tapa havainnollistaa tämä käyttämällä taas esimerkkinä tavoitetta 18:
| 2n | 24 | 23 | 22 | 21 | 20 | 18 – 16 = 2 | → | 2 – 2 = 0 |
Muunnos binäärijärjestelmästä desimaalijärjestelmään on yksinkertaisempi. Määritä kaikki paikka-arvot, joissa 1 esiintyy, ja etsi arvojen summa.
EX: 10111 = (1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20) = 23
| 24 | 23 | 22 | 21 | 20 | |
| 1 | 0 | 1 | 1 | 1 | |
| 16 | 0 | 4 | 4 | 2 | 1 |
Selv: 16 + 4 + 2 + 1 = 23.
Binäärinen yhteenlasku
Binäärinen yhteenlasku noudattaa samoja sääntöjä kuin yhteenlasku desimaalijärjestelmässä, paitsi että sen sijaan, että ykköstä ei siirretä, kun yhteenlasketut arvot ovat yhtä suuret kuin 10, siirto tapahtuu, kun yhteenlaskun tulos on yhtä suuri kuin 2. Katso selvennystä alla olevasta esimerkistä.
Huomaa, että binäärijärjestelmässä:
- 0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0, siirretään 1, ts. 10
EX:
| 10 | 11 | 11 | 10 | 1 | |||
| = | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Ainut varsinainen ero binääri- ja desimaalilaskennan yhteenlaskun välillä on se, että arvo 2 binäärijärjestelmässä vastaa 10:tä desimaalijärjestelmässä. Huomaa, että yliviivatut ykköset edustavat numeroita, jotka siirretään. Yleinen virhe, jota kannattaa varoa binääristä yhteenlaskutoimitusta suoritettaessa, on tapaus, jossa 1 + 1 = 0:n oikealla puolella olevasta edellisestä sarakkeesta on myös siirretty ykkönen. Tällöin alhaalla olevan arvon pitäisi olla siirtyneestä 1:stä peräisin oleva 1 eikä 0. Tämä voidaan havaita yllä olevan esimerkin kolmannessa sarakkeessa oikealta.
Binäärinen vähennyslasku
Samoin kuin binäärisessä yhteenlaskussa, binäärisen ja desimaalisen vähennyslaskun välillä ei ole juurikaan eroja, lukuun ottamatta niitä, jotka johtuvat siitä, että käytetään vain numeroita 0 ja 1. Lainaamista tapahtuu aina, kun vähennettävä luku on suurempi kuin luku, josta se vähennetään. Binäärisessä vähennyslaskussa lainaaminen on tarpeen vain silloin, kun 1 vähennetään 0:sta. Tällöin lainattavan sarakkeen 0:sta tulee periaatteessa ”2” (jolloin 0-1 muuttuu 2-1 = 1:ksi), kun taas lainattavan sarakkeen 1 vähenee 1:llä. Jos seuraava sarake on myös 0, lainaaminen on tehtävä jokaisesta seuraavasta sarakkeesta, kunnes sarake, jonka arvo on 1, voidaan vähentää 0:ksi. Selvennystä saa alla olevasta esimerkistä.
Huomaa, että binäärisessä järjestelmässä:
- 0 – 0 = 0
0 – 1 = 1, lainataan 1, jolloin saadaan -1 siirrettyä
1 – 0 = 1
1 – 1 = 0
EX1:
| -11 | 20 | 1 | 1 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| – | 0 | 1 | 1 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -11 | 2-10 | 0 | ||
| – | 0 | 1 | 1 | |
| = | 0 | 0 | 1 | |
Huomaa, että näkyvät yliviivat ovat muutoksia, jotka tapahtuvat kuhunkin bittiin lainattaessa. Lainaava sarake saa lainaamisesta periaatteessa 2, ja sarake, josta lainataan, pienenee 1:llä.
Binäärikertolasku
Binäärikertolasku on kiistatta yksinkertaisempi kuin sen desimaalinen vastine. Koska ainoat käytetyt arvot ovat 0 ja 1, yhteenlaskettavat tulokset ovat joko sama kuin ensimmäinen termi tai 0. Huomaa, että jokaisella seuraavalla rivillä on lisättävä nollat ja arvo on siirrettävä vasemmalle, aivan kuten desimaalikertolaskussa. Binäärikertolaskun monimutkaisuus johtuu työlästä binäärilisäyksestä, joka riippuu siitä, kuinka monta bittiä kussakin termissä on. Katso selvennystä alla olevasta esimerkistä.
Huomaa, että binäärijärjestelmässä:
- 0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
EX:
| 1 | 0 | 1 | 1 | 1 | ||||
| × | 1 | 1 | ||||||
| 1 | 0 | 1 | 1 | 1 | ||||
| + | 1 | 0 | 1 | 1 | 1 | 0 | ||
| = | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Kuten yllä olevasta esimerkistä voidaan nähdä, binäärisen kertolaskun prosessi on sama kuin desimaalisen kertolaskun. Huomaa, että toiselle riville on kirjoitettu 0-paikanvaraaja. Tyypillisesti 0-merkki ei ole näkyvissä desimaalikertolaskussa. Vaikka sama voidaan tehdä tässäkin esimerkissä (jolloin 0-paikanvaraaja oletetaan nimenomaisen sijasta), se on sisällytetty tähän esimerkkiin, koska 0 on merkityksellinen missä tahansa binäärisessä yhteenlasku- / vähennyslaskulaskimessa, kuten tällä sivulla esitetyssä laskimessa. Ilman 0:n esittämistä olisi mahdollista erehtyä jättämään 0 pois, kun edellä esitettyjä binääriarvoja lasketaan yhteen. Huomaa jälleen, että binäärijärjestelmässä kaikki 1:n oikealla puolella olevat 0:t ovat merkityksellisiä, kun taas kaikki arvon viimeisen 1:n vasemmalla puolella olevat 0:t eivät ole.
EX:
- 1 0 1 0 1 1 1 0 0
= 0 0 1 0 1 0 1 1 1 0 0
≠ 1 0 1 0 1 1 1 0 0 0 0 0
Binäärijako
Binäärijako on samanlainen kuin pitkä jako desimaalijärjestelmässä. Jakaja jaetaan edelleen jakajaan samalla tavalla, ja ainoa merkittävä ero on se, että käytetään binääristä eikä desimaalista vähennyslaskentaa. Huomaa, että binäärisen vähennyslaskun hyvä ymmärtäminen on tärkeää binäärijaon suorittamisessa. Tutustu alla olevaan esimerkkiin sekä binääristä vähennyslaskentaa käsittelevään jaksoon selvennyksen saamiseksi.