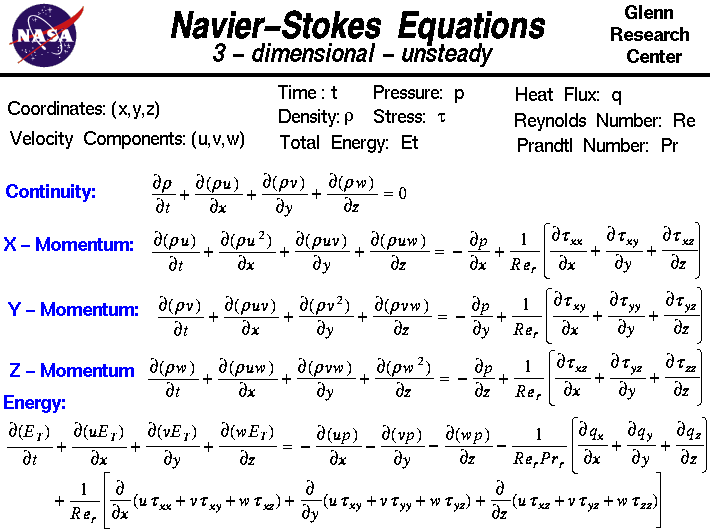
Cette diapositive montre la forme instationnaire tridimensionnelle des équations de Navier-Stokes.Ces équations décrivent comment la vitesse, la pression, la température et la densité d’un fluide en mouvement sont liées.Les équations ont été dérivées indépendamment par G.G. Stokes, en Angleterre, et M. Navier, en France, au début des années 1800. Navier, en France, au début des années 1800.Ces équations sont des extensions des équations d’Euler et incluent les effets de la viscosité sur l’écoulement.Ces équations sont très complexes, mais les étudiants de premier cycle en ingénierie apprennent à les dériver selon un processus très similaire à la dérivation que nous présentons sur la page Web de la conservation de la quantité de mouvement.
Les équations sont un ensemble d’équations différentielles couplées et pourraient, en théorie, être résolues pour un problème d’écoulement donné en utilisant des méthodes de calcul.Mais, en pratique, ces équations sont trop difficiles à résoudre analytiquement.Dans le passé, les ingénieurs faisaient d’autres approximations et simplifications de l’ensemble des équations jusqu’à ce qu’ils aient un groupe d’équations qu’ils pouvaient résoudre.Récemment, des ordinateurs à haute vitesse ont été utilisés pour résoudre des approximations des équations en utilisant une variété de techniques comme les différences finies, les volumes finis, les éléments finis et les méthodes spectrales.Ce domaine d’étude est appelé Computational Fluid Dynamics ou CFD.
Les équations de Navier-Stokes consistent en une équation de continuité dépendant du temps pour la conservation de la masse, trois équations de conservation de momentume dépendant du temps et une équation de conservation d’énergie dépendant du temps.Il y a quatre variables indépendantes dans le problème, les coordonnées spatialesx, y et z d’un certain domaine, et le temps t. Il y a six variables dépendantes : la pression p, la densité r et la température T (qui est contenue dans l’équation d’énergie par le biais de l’énergie totale Et) et trois composantes du vecteur vitesse : la composante u est dans la direction x, la composante v est dans la direction y et la composante w est dans la direction z. Toutes les variables dépendantes sont des fonctions des quatre variables indépendantes.Les équations différentielles sont donc des équations différentielles partielleset non les équations différentielles ordinaires que vous étudiez dans un cours de calcul débutant.
Vous remarquerez que le symbole différentiel est différent de l’habituel « d /dt » ou « d /dx » que vous voyez pour les équations différentielles ordinaires. Le symbole « 
» est utilisé pour indiquer les dérivées partielles.Le symbole indique que nous devons maintenir toutes les variables indépendantes fixes, sauf la variable à côté du symbole, lors du calcul d’une dérivée. Le jeu d’équations est :
Continuité : r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momentum : (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – Momentum : (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momentum : (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Énergie : Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
où Re est le nombre deReynoldsqui est un paramètre de similarité qui est le rapport de l’échelle de linertie de l’écoulement aux forces visqueuses dans l’écoulement. Les variables q sont les composantes du flux thermique et Pr est le nombre de Prandtl qui est un paramètre de similarité représentant le rapport entre les contraintes visqueuses et les contraintes thermiques.Les variables tau sont les composantes du tenseur des contraintes.Un tenseur est généré lorsque vous multipliez deux vecteurs d’une certaine manière. Notre vecteur vitesse a trois composantes ; le tenseur des contraintes a neuf composantes. Chaque composante du tenseur de contrainte est elle-même une dérivée seconde des composantes de la vitesse.
Les termes du côté gauche des équations de la quantité de mouvement sont appelés les termes de convection des équations.La convection est un processus physique qui se produit dans un flux de gaz dans lequel une certaine propriété est transportée par le mouvement ordonné du flux.Les termes du côté droit des équations de la quantité de mouvement qui sont multipliés par le nombre inverse de Reynolds sont appelés termes de diffusion.La diffusion est un processus physique qui se produit dans un écoulement de gaz dans lequel une certaine propriété est transportée par le mouvement aléatoire des molécules du gaz.La diffusion est liée au tenseur des contraintes et à la viscosité du gaz. La diffusion est liée au tenseur des contraintes et à la viscosité du gaz. La turbulence et la génération de couches limites sont le résultat de la diffusion dans l’écoulement. Les équations d’Euler ne contiennent que les termes de convection des équations de Navier-Stokes et ne peuvent donc pas modéliser les couches limites. Il existe une simplification spéciale des équations de Navier-Stokes qui décrivent les écoulements de couches limites.
Notez que toutes les variables dépendantes apparaissent dans chaque équation.Pour résoudre un problème d’écoulement, vous devez résoudre les cinq équations simultanément ; c’est pourquoi nous appelons cela un système couplé d’équations.Il y a en fait quelques autres équations qui sont nécessaires pour résoudre ce système. Nous ne montrons que cinq équations pour six inconnues. Une équation d’état relie la pression, la température et la densité du gaz.Et nous devons spécifier tous les termes du tenseur de contrainte.En CFD, les termes du tenseur de contrainte sont souvent approximés par un modèle de turbulence.
Activités:
Visites guidées
Navigation ..
Page d’accueil du guide du débutant.