L’analyse amortie est utilisée pour les algorithmes qui ont des opérations coûteuses qui ne se produisent que rarement.

L’analyse de complexité amortie est le plus souvent utilisée avec des structures de données qui ont un état qui persiste entre les opérations.L’idée de base est qu’une opération coûteuse peut modifier l’état de sorte que le pire cas ne peut pas se reproduire pendant une longue période, amortissant ainsi son coût.
Laissez T1, T2, …, Tk être les complexitésd’une séquence d’opérations sur une structure de données. La complexité amortie d’une opération unique dans cette séquence est(T1 + T2 + …+ Tk) / k.
Exemple : un tableau dynamique
Dans un tableau dynamique,les éléments sont stockés au début d’un tableau fixe sous-jacent,et les positions restantes sont inutilisées.
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Voici une vue de la mémoire lors de l’ajout des éléments 2, 7, 1, 3, 8, 4à un tableau initialement vide de capacité 2.
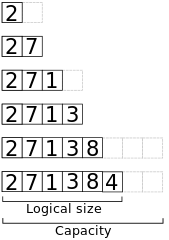
Temps dans le pire des cas
La complexité en temps dans le pire des cas pour l’ajout d’un élément à un tableau de longueur n, en utilisant cet algorithme, est Θ(n).Si le tableau est plein, l’algorithme alloue un nouveau tableau de longueur 2n, puis copie les éléments de l’ancien tableau dans le nouveau.
Ce résultat est excessivement pessimiste.Les n opérations d’ajout suivantes seront beaucoup moins coûteuses -chacune d’entre elles s’exécutera en temps constant puisque le tableau nouvellement alloué a de la place pour tous les nouveaux éléments.
Temps amorti
Une analyse du temps amorti permet de bien mieux comprendre l’algorithme.
Considérons une séquence de n opérations d’ajout,où nous commençons avec un tableau de longueur 1. Une analyse attentive montre que le temps total de ces opérations n’est que Θ(n).
- Il y aura un total de n opérations d’affectation et d’incrémentation à temps constant.
- Le redimensionnement n’aura lieu qu’à l’opération 1, 2, 4, …, 2k, pour un total de 1 + 2 + 4 + …+ 2k = 2-2k – 1 opérations de copie d’éléments à temps constant. Puisque 2k ≤ n, c’est au plus 2n – 1.
Hence, la complexité temporelle amortie pour une seule opération d’ajout est Θ(1).
Plus sur l’analyse des algorithmes

Complexité temporelle : Comptez vos pas

Notation Big O
.