Une couche limite est une mince couche de fluide visqueux proche de la surface solide d’une paroi en contact avec un courant en mouvement dans laquelle (dans son épaisseur δ) la vitesse de l’écoulement varie de zéro à la paroi (où l’écoulement « colle » à la paroi à cause de sa viscosité) jusqu’à Ue à la limite, ce qui correspond approximativement (à 1% d’erreur près) à la vitesse du courant libre (voir figure 1). A proprement parler, la valeur de δ est une valeur arbitraire car la force de friction, dépendant de l’interaction moléculaire entre le fluide et le corps solide, diminue avec la distance à la paroi et devient égale à zéro à l’infini.
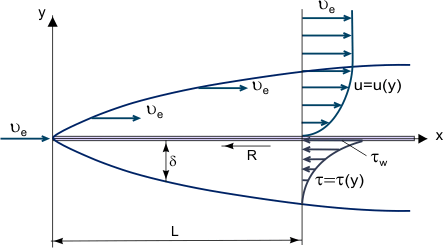
Figure 1. Croissance d’une couche limite sur une plaque plane.
Le concept fondamental de la couche limite a été suggéré par L. Prandtl (1904), il définit la couche limite comme une couche de fluide se développant dans des écoulements avec des nombres de Reynolds Re très élevés, c’est-à-dire avec une viscosité relativement faible par rapport aux forces d’inertie. Ce phénomène est observé lorsque des corps sont exposés à un courant d’air à grande vitesse ou lorsque des corps sont très grands et que la vitesse du courant d’air est modérée. Dans ce cas, dans une couche limite relativement mince, la contrainte de cisaillement par friction (force de cisaillement visqueuse) : τ = η (où η est la viscosité dynamique ; u = u(y) – « profil » de la composante de vitesse longitudinale de la couche limite, voir la figure 1) peut être très grande ; en particulier, à la paroi où u = 0 et τw = ηw bien que la viscosité elle-même puisse être plutôt faible.
Il est possible d’ignorer les forces de frottement à l’extérieur de la couche limite (par rapport aux forces d’inertie), et sur la base du concept de Prandtl, de considérer deux régions d’écoulement : la couche limite où les effets de frottement sont importants et le noyau d’écoulement presque Inviscide. En partant du principe que la couche limite est une couche très mince (δ << L, où L est la dimension linéaire caractéristique du corps sur lequel se produit l’écoulement ou du canal contenant l’écoulement, son épaisseur diminuant avec la croissance de Re, figure 1), on peut estimer l’ordre de grandeur de l’épaisseur de la couche limite à partir de la relation suivante :
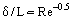
Par exemple, lorsqu’un avion vole à Ue = 400 km/h, l’épaisseur de la couche limite au bord de fuite de l’aile avec une corde de 1 mètre (longueur du profil) est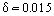 m. Comme cela a été établi expérimentalement, une couche limite laminaire se développe à la section d’entrée du corps. Progressivement, sous l’influence de certains facteurs déstabilisants, la couche limite devient instable et la transition de la couche limite vers un régime d’écoulement turbulent a lieu. Des études expérimentales spéciales ont établi l’existence d’une région de transition entre les régions turbulente et laminaire. Dans certains cas (par exemple, lorsque le niveau de turbulence de l’écoulement externe est élevé), la couche limite devient turbulente immédiatement en aval du point de stagnation de l’écoulement. Dans certaines conditions, comme une forte chute de pression, un phénomène inverse se produit dans les écoulements turbulents accélérés, à savoir la relaminarisation de l’écoulement.
m. Comme cela a été établi expérimentalement, une couche limite laminaire se développe à la section d’entrée du corps. Progressivement, sous l’influence de certains facteurs déstabilisants, la couche limite devient instable et la transition de la couche limite vers un régime d’écoulement turbulent a lieu. Des études expérimentales spéciales ont établi l’existence d’une région de transition entre les régions turbulente et laminaire. Dans certains cas (par exemple, lorsque le niveau de turbulence de l’écoulement externe est élevé), la couche limite devient turbulente immédiatement en aval du point de stagnation de l’écoulement. Dans certaines conditions, comme une forte chute de pression, un phénomène inverse se produit dans les écoulements turbulents accélérés, à savoir la relaminarisation de l’écoulement.
En dépit de sa relative minceur, la couche limite est très importante pour initier les processus d’interaction dynamique entre l’écoulement et le corps. La couche limite détermine la traînée et la portance aérodynamiques du véhicule volant, ou la perte d’énergie pour l’écoulement des fluides dans les canaux (dans ce cas, une couche limite hydrodynamique car il y a aussi une couche limite thermique qui détermine l’interaction thermodynamique du Transfert de chaleur).
Le calcul des paramètres de la couche limite est basé sur la résolution des équations obtenues à partir des équations de Navier-Stokes pour le mouvement des fluides visqueux, qui sont d’abord considérablement simplifiées en tenant compte de la minceur de la couche limite.
La solution suggérée par L. Prandtl est essentiellement le premier terme de l’expansion en série de puissance de l’équation de Navier-Stokes, l’expansion en série étant effectuée pour les puissances du paramètre sans dimension (δ/L). Le plus petit paramètre dans ce terme est à la puissance zéro de sorte que l’équation de la couche limite est l’approximation zéro dans une expansion asymptotique (à grand Re) de l’équation de la couche limite (solution asymptotique).
Une transformation de l’équation de Navier-Stokes en équations de la couche limite peut être démontrée en dérivant l’équation de Prandtl pour la couche limite laminaire dans un écoulement incompressible bidimensionnel sans forces de corps.
Dans ce cas, le système d’équations de Navier-Stokes sera :

Après avoir évalué l’ordre de grandeur de certains termes de l’équation. (2) et en ignorant les petits termes, le système d’équations de Prandtl pour la couche limite laminaire devient :

dans lesquelles x, y sont des coordonnées longitudinales et latérales (figure 1) ; v est la composante de vitesse le long de l’axe « y » ; p, la pression ; t, le temps ; et n la viscosité cinématique.
La couche limite est mince et la vitesse à son bord externe Ue peut être déterminée de manière suffisante et précise comme la vitesse d’un écoulement fluide idéal (inviscide) le long de la paroi calculée jusqu’à la première approximation, sans tenir compte de l’action inverse de la couche limite sur l’écoulement externe. Le gradient de pression longitudinal = (à p(y) = const) dans l’équation (3) peut être représenté à partir de l’équation d’Euler du mouvement d’un fluide idéal. A partir de ce qui précède, les équations de Prandtl sous leur forme finie s’écriront comme suit :

Il s’agit d’un système d’équations différentielles partielles paraboliques non linéaires du second ordre qui sont résolues avec des conditions initiales et limites


Le système d’équations (4) est écrit pour des valeurs réelles des composantes de vitesse u et v. Pour généraliser les équations obtenues pour les écoulements turbulents, il faut utiliser la relation bien connue entre les composantes réelles, moyennes et pulsées des paramètres des écoulements turbulents. Par exemple, pour les composantes de vitesse, il existe des relations reliant les composantes réelles u et v, moyennes ū et et pulsantes u’ et v’ :
et pulsantes u’ et v’ :

Après quelques réarrangements, il est possible d’obtenir un autre système d’équations à partir du système (3), notamment pour un écoulement stationnaire :
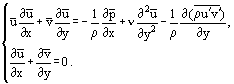
En utilisant la relation suivante pour la contrainte de cisaillement par friction dans la couche limite :
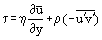
et en tenant compte du fait que dans la couche limite laminaire u = u’ et il est possible de réécrire les équations de Prandtl sous une forme valable pour les écoulements laminaires et turbulents :
il est possible de réécrire les équations de Prandtl sous une forme valable pour les écoulements laminaires et turbulents :
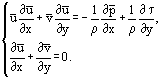
Les solutions les plus simples ont été obtenues pour une couche limite laminaire sur une plaque plane mince dans un écoulement parallèle bidimensionnel de fluide incompressible (figure 1). Dans ce cas, l’estimation de l’ordre de grandeur des termes des équations : x ~ L, y ~ δ, δ ~ permet de combiner les variables x et y dans une seule relation
permet de combiner les variables x et y dans une seule relation

et de réduire la solution de l’équation (8) (à dp/dx = 0) à la détermination des dépendances de u et v vis-à-vis du nouveau paramètre ξ. D’autre part, en utilisant les relations bien connues entre les composantes de la vitesse u, v et la fonction du courant ψ

il est possible d’obtenir une seule équation différentielle ordinaire non linéaire du troisième ordre, au lieu du système d’équations différentielles partielles (8)

Ici, f(ξ) est la fonction inconnue de la variable ξ : f = ƒ =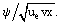
La première solution numérique de l’équation. (10) a été obtenue par Blasius (1908) dans des conditions aux limites correspondant aux conditions physiques de la couche limite en y = 0 : u = 0, v = 0 ; en y → ∞ ; u → Ue (couche limite de Blasius).
La figure 2 compare les résultats de la solution de Blasius (ligne pleine) avec les données expérimentales. En utilisant ces données, il est possible d’évaluer l’épaisseur de la couche limite visqueuse. À ξ  2,5, (u/Ue
2,5, (u/Ue 0,99) (figure 2) ; par conséquent, à partir de l’équation (9), nous obtenons:
0,99) (figure 2) ; par conséquent, à partir de l’équation (9), nous obtenons:

Figure 2.
D’après les calculs numériques de Blasius de la valeur de la dérivée seconde de la fonction f(ξ) à la contrainte de cisaillement par frottement sur la paroi, la relation dans ce cas est :

La force de frottement R, agissant sur les deux côtés de la plaque de longueur L (figure 1), est également déterminée à partir de l’équation. (11):

comme le coefficient de frottement pour les plaques plates:
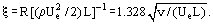
Malgré le fait que les équations de Prandtl sont beaucoup plus simples que les équations de Navier-Stokes, leurs solutions ont été obtenues pour un nombre limité de problèmes. Pour de nombreux problèmes pratiques, il n’est pas nécessaire de déterminer les profils de vitesse dans la couche limite, seulement l’épaisseur et la contrainte de cisaillement. Ce genre d’information peut être obtenu en résolvant l’équation intégrale de la quantité de mouvement

La relation intégrale (12) est valable à la fois pour la couche limite laminaire et turbulente.
Les fonctions qui n’étaient pas connues a priori mais qui caractérisent la distribution des paramètres du fluide à travers l’épaisseur δ de la couche sont sous l’intégrale de l’équation (12). Et l’erreur de calcul de l’intégrale est inférieure à l’erreur dans la fonction intégrande approximativement supposée ρu = ρu(y). Ces conditions permettent de développer des méthodes approximatives de calcul des paramètres de la couche limite qui prennent moins de temps que les méthodes exactes d’intégration des équations de Prandtl. Le concept fondamental a été suggéré pour la première fois par T. von Karman, qui a introduit une telle épaisseur de couche arbitraire δ*
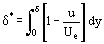
et une épaisseur de déplacement de la quantité de mouvement δ**
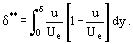
ainsi, nous pouvons transformer Eq. (12) pour une couche limite bidimensionnelle de fluide incompressible en:

Il y a trois fonctions inconnues dans l’équation (15), à savoir, δ* = δ*(x), δ** = δ**(x) et τw = τw(x) .
La solution d’une équation différentielle ordinaire comme Eq. (15) nécessite généralement l’hypothèse (ou la représentation) de la distribution de la vitesse (profil de vitesse) à travers l’épaisseur de la couche limite en fonction de certains paramètres caractéristiques (paramètres de forme), et elle nécessite également l’utilisation de données empiriques sur la relation entre le coefficient de friction Cf = 2τw/(ρU2e) et l’épaisseur arbitraire de la couche limite (loi de friction).
Certaines explications physiques définies peuvent être données en ce qui concerne les valeurs de δ* et δ**. La fonction intégrande de l’équation (13) contient après réarrangement, un terme (Ue – u) qui caractérise la diminution de la vitesse. L’intégrale de l’équation (14) peut donc être considérée comme une mesure de la diminution du débit à travers la couche limite, par rapport à l’écoulement parfait du fluide à la vitesse Ue. D’autre part, la valeur de δ* peut être considérée comme la mesure de la déviation le long d’une normale à la paroi (selon l’axe « y ») de la ligne d’écoulement externe sous l’influence des forces de friction. De cette considération de la structure intégrale de l’équation (14), il est possible de conclure que δ** caractérise la diminution de la quantité de mouvement dans la couche limite sous l’influence de la friction.
Les relations suivantes sont valables :

où H est le paramètre de forme du profil de vitesse de la couche limite. Par exemple, pour une distribution linéaire u = ky,
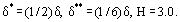
À l’heure actuelle, les théories dites semi-empiriques sont largement utilisées pour prédire les paramètres de la couche limite turbulente. Dans ce cas, on suppose que la contrainte de frottement totale τ dans une couche limite turbulente est une somme

Ici, τT est la contrainte de frottement supplémentaire (turbulente ou Reynolds), en particulier, dans un écoulement incompressible voir Eq. (7).
voir Eq. (7).
Cette représentation est directement liée au système d’équations du mouvement dans la couche limite (6). Dans la couche limite compressible, les pulsations de densité peuvent être considérées comme le résultat de pulsations de température

où β = (1/T) est le coefficient de dilatation volumétrique.
Des hypothèses semi-empiriques supplémentaires sur le transfert de quantité de mouvement turbulent sont utilisées pour déterminer τT. Par exemple,

où ηT est le coefficient dynamique de viscosité turbulente introduit par J. Boussinesq en 1877.
Sur la base du concept de similarité des échanges moléculaires et turbulents (théorie de la similarité), Prandtl a introduit l’hypothèse de la longueur de mélange (die Mischungsweg). La longueur de mélange 1 est le chemin qu’un volume de fluide fini (« mole ») passe d’une couche de mouvement moyen à une autre sans changer sa quantité de mouvement. Conformément à cette condition, il a dérivé une équation qui s’est avérée fondamentale pour la théorie de la couche limite:

Pour la région turbulente de la couche limite d’écoulement près de la paroi, L. Prandtl a considéré la longueur 1 proportionnelle à y

où κ est une constante empirique.
Près de la paroi, où ηT << η, le frottement moléculaire visqueux est un facteur déterminant. L’épaisseur de cette partie de la couche limite δ1, que l’on appelle sous-couche laminaire ou visqueuse, est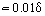 . En dehors de la sous-couche, la valeur de ηT augmente, atteignant plusieurs ordres de grandeur supérieurs à η. Corrélativement, dans cette zone de la couche limite appelée noyau turbulent, τT > 0 = η. Parfois, le noyau turbulent est subdivisé en zone tampon, où les frottements laminaire et turbulent ont une valeur comparable, et en zone développée, où τT >> τ0. Pour cette région, après avoir intégré l’équation (18) et en tenant compte de l’équation (19), il est possible de dériver une expression pour le profil de vitesse logarithmique :
. En dehors de la sous-couche, la valeur de ηT augmente, atteignant plusieurs ordres de grandeur supérieurs à η. Corrélativement, dans cette zone de la couche limite appelée noyau turbulent, τT > 0 = η. Parfois, le noyau turbulent est subdivisé en zone tampon, où les frottements laminaire et turbulent ont une valeur comparable, et en zone développée, où τT >> τ0. Pour cette région, après avoir intégré l’équation (18) et en tenant compte de l’équation (19), il est possible de dériver une expression pour le profil de vitesse logarithmique :
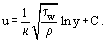
Si l’on utilise des coordonnées sans dimension (ou universelles).

où est la vitesse dite dynamique (ou vitesse de friction), l’équation. (20) peut être réécrite sous la forme suivante :
est la vitesse dite dynamique (ou vitesse de friction), l’équation. (20) peut être réécrite sous la forme suivante :
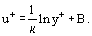
La représentation de la distribution de la vitesse en coordonnées universelles et les modèles mathématiques pour le coefficient de viscosité turbulent sont traités plus en détail dans la section de l’écoulement turbulent.
L’une des versions actuelles de la théorie semi-empirique de la couche limite turbulente développée par S. S. Kutateladze et A. I. Leontiev est basée sur la théorie dite asymptotique des couches limites turbulentes à Re → ∞ où l’épaisseur de la sous-couche laminaire (visqueuse) δ1 diminue à un taux plus élevé que δ en conséquence de quoi (δ1/δ) → 0.
Dans ces conditions, une couche limite turbulente avec une « viscosité de fuite » se développe. Dans cette couche, η → 0 mais n’est pas égal à zéro et à cet égard, la couche diffère de l’écoulement fluide parfait. Le concept de loi de friction relative, introduit par S. S. Kutateladze et A. I. Leontiev (1990), indique
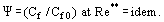
La loi est définie comme le rapport entre le coefficient de friction Cf pour la condition considérée et la valeur de Cf0 pour des conditions « standard » sur une plaque plate et imperméable parcourue par un écoulement incompressible et isotherme, les deux coefficients étant obtenus pour Re** = Ueδ**/ν. Il est démontré qu’à Re → ∞ ; η → 0 ; et Cf → 0, la variation relative du coefficient de frottement sous l’influence de facteurs perturbateurs tels que le gradient de pression, la compressibilité, la non-isothermicité, l’injection (aspiration) à travers une paroi poreuse, etc. a une valeur finie.
Les équations dérivées pour calculer la valeur de Ψ ont une caractéristique importante qui rend Ψ indépendant des constantes empiriques de la turbulence. Conformément au concept fondamental de l' »approche » intégrale, l’équation intégrale de la quantité de mouvement est transformée en :
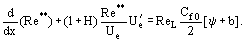
Ici, ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) sont les paramètres de perméabilité pour le cas de l’injection d’un gaz de densité ρw à travers une paroi perméable à la vitesse de vw. Pour déterminer la fonction Re** = Re**
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) sont les paramètres de perméabilité pour le cas de l’injection d’un gaz de densité ρw à travers une paroi perméable à la vitesse de vw. Pour déterminer la fonction Re** = Re** , il est nécessaire de calculer la distribution
, il est nécessaire de calculer la distribution Pour cela, le principe de superposition des facteurs perturbateurs s’applique
Pour cela, le principe de superposition des facteurs perturbateurs s’applique

Dans l’équation. 24, chaque multiplicateur représente la loi de friction relative, en tenant compte de l’effet d’un des facteurs, parmi lesquels la compressibilité ΨM, la tête de température (ou Enthalpie) ΨT, l’injection ΨB, le gradient de pression ΨP et autres.
Les concepts fondamentaux de la couche limite créent les conditions pour expliquer des phénomènes tels que la séparation de l’écoulement de la surface sous l’influence de l’inertie de l’écoulement, la décélération de l’écoulement visqueux par la paroi et le gradient de pression défavorable agissant dans la direction amont = 0 ou < 0.
Si le gradient de pression est défavorable à l’emplacement de la surface entre les sections ‘1-4’ (voir figure 3), la distribution des vitesses u = u(x,y) dans la couche limite change progressivement ; devenant « moins pleine », diminuant l’inclinaison dans les jets de fluide qui sont plus proches de la paroi et possédant moins d’énergie cinétique (voir les formes de profil de vitesse sur la figure 3) qui pénètrent loin en aval dans la région de pression accrue. Dans certaines sections, par exemple la section ‘4’, les particules de fluide qui se trouvent sur la ligne de courant ‘a-a’ (ligne pointillée sur la figure 3) – ayant complètement épuisé leur réserve d’énergie cinétique deviennent décélérées (ua = 0).
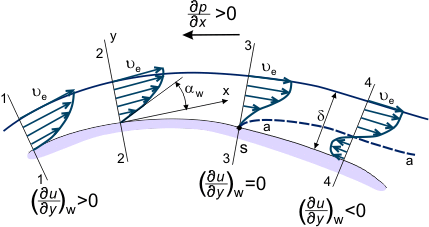
Figure 3. Couche limite dans un écoulement sur une surface couverte.
La pression statique et la valeur du gradient de pression ne varient pas sur l’épaisseur de la couche limite. Par conséquent, les particules de fluide qui sont plus proches de la paroi que la ligne ‘a-a’ et qui possèdent encore moins d’énergie commencent à se déplacer dans la direction opposée sous l’influence du gradient de pression dans la section ‘4-4’ (voir figure 3). Ainsi, la relation :

De cette manière, à certains endroits de la surface, le profil de vitesse change. Ce changement est caractérisé par l’altération du signe de la dérivée w, qui passe d’un signe positif (section 2, figure 3) à un signe négatif (section 4). Bien entendu, il est également possible de définir la section où w = 0 (section 3, figure 3). Cette section est appelée section de séparation de la couche limite (le point « S » sur la surface de cette section est le point de séparation). Elle se caractérise par le développement d’une zone d’écoulement inverse – l’écoulement autour du corps n’est plus lisse, la couche limite devient considérablement plus épaisse et les lignes d’écoulement externes s’écartent de la surface du corps survolé. En aval du point de séparation, la distribution de la pression statique dans l’épaisseur de la couche n’est pas régulière et la distribution de la pression statique le long de la surface ne correspond pas à la distribution de la pression dans l’écoulement externe, inviscide.
La séparation est suivie par le développement de zones d’écoulement inverse et de tourbillons, dans lesquels l’énergie cinétique fournie par l’écoulement externe se transforme en chaleur sous l’influence des forces de friction. La séparation des écoulements, accompagnée d’une dissipation d’énergie dans les zones de tourbillon à écoulement inverse, entraîne des effets indésirables tels que l’augmentation de la traînée des véhicules volants ou des pertes hydrauliques dans les canaux.
D’autre part, les écoulements séparés sont utilisés dans différents dispositifs de mélange intensif de fluide (par exemple, pour améliorer le mélange du carburant et de l’air dans les chambres de combustion des moteurs). Lorsque des fluides visqueux s’écoulent dans des canaux à section variable (gradient de pression alternatif), la zone de séparation peut être locale si la section du diffuseur est suivie de la section du confusor, où l’écoulement séparé se rattache à nouveau à la surface (voir figure 4a). Lorsque l’écoulement se sépare du bord de fuite du corps (par exemple, du bord de fuite de l’aile), ce qu’on appelle le sillage est formé par des couches limites « liantes » (voir figure 4b).
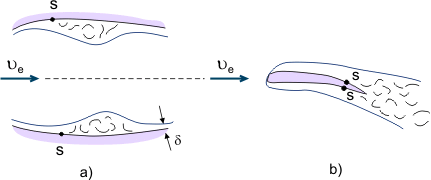
Figure 4. Phénomènes de séparation des couches limites.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung : Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung : Z. Math. Phys., 56:1-37.
Kutateladze, S. S. et Leontiev, A. I. (1990) Transfert thermique, transfert de masse et couches limites turbulentes, Hemisphere Publishing Corporation, New York, Washington, Philadelphie, Londres.