Sun, 18 Jun 2006
1+1=2
Les Principia Mathematica de Whitehead et Russell sont célèbres pour avoir pris mille pages pour prouver que 1+1=2. Bien sûr, il prouve aussi beaucoup d’autres choses. S’ils avaient voulu prouver seulement que 1+1=2, cela aurait probablement pris moitié moins d’espace.
Principia Mathematica est un livre étrange, qui vaut la peine d’être examiné d’un point de vue historique aussi bien que mathématique. Il a été écrit vers 1910, et la logique mathématique était alors encore à ses débuts, fraîchement transformée par Peano et Frege. La notation est quelque peu obscure, car la notation mathématique a considérablement évolué depuis lors. Et de nombreuses techniques simples que nous considérons aujourd’hui comme acquises sont absentes.Comme un programme informatique mal écrit, une grande partie de la masse des Principia Mathematica est constituée de codes répétés, de sections séparées qui disent essentiellement les mêmes choses, parce que les auteurs n’ont pas encore appris les techniques qui permettraient de combiner ces sections en une seule.
Par exemple, la section ∗22, « Calcul des classes », commence par définir la relation de sous-ensemble (∗22.01), et les opérations d’union et d’intersection d’ensembles (∗22.02 et .03), le complément d’un ensemble (∗22.04), et la différence de deux ensembles (∗22.05). Il prouve ensuite la commutativité et l’associativité de l’union et de l’intersection d’ensembles (∗22.51, .52, .57, et .7), diverses propriétés comme !!\alpha\cap\alpha = \alpha ! !! (∗22.5) et autres, en travaillant jusqu’à des théorèmes comme ∗22.92 : !!\alpha\subset\beta \rightarrow \alpha\cup(\beta -\alpha) !!.
La section ∗23 est « Calcul des relations » et commence presque exactement de la même manière, en définissant la relation de sous-rélation (∗23.01), et les opérations d’union et d’intersection relationnelles (∗23.02 et .03), le complément d’une relation (∗23.04), et la différence de deux relations (∗23.05). Il prouve ensuite la commutativité et l’associativité de l’union et de l’intersection relationnelles (∗23.51, .52, .57, et .7), diverses propriétés comme !!\alpha\dot\cap\alpha = \alpha ! !! (∗22.5) et autres, jusqu’à des théorèmes comme ∗23.92 : !\alpha\dot\subset\beta \rightarrow \alpha\dot\cup(\beta \dot-\alpha) !!.
La section ∗24 porte sur l’existence d’ensembles, l’ensemble nul !\Lambda !!, l’ensemble universel !{\rm V} !!!, leurs propriétés, et ainsi de suite, et ensuite la section ∗24 est dupliquée en ∗25 dans une série de théorèmes sur l’existence des relations, la relation nulle !\dot\Lambda !!, la relation universelle !\dot {\rm V} !!,leurs propriétés, et ainsi de suite.
C’est ainsi que Whitehead et Russell ont procédé en 1910. Comment le ferions-nous aujourd’hui ? Une relation entre S et T est définie comme un sous-ensemble deS × T et est donc un ensemble. L’union, l’intersection, la différence et les autres opérations sont précisément les mêmes pour les relations que pour les ensembles, car les relations sont des ensembles. Tous les théorèmes sur les unions et les intersections de relations, comme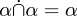 
, disparaissent, car nous les avons déjà prouvés pour les ensembles et les relations sont des ensembles. La relation nulle est l’ensemble nul. La relation universelle est l’ensemble universel.
Une énorme quantité d’autres machines disparaît en 2006, à cause de l’unification des relations et des ensembles. Principia Mathematica a besoin d’une notation spéciale et d’une définition spéciale pour le résultat de la restriction d’une relation aux paires dont le premier élément est un membre d’un ensemble particulier S, ou dont le second élément est un membre de S, ou dont les deux éléments sont des membres de S ; en 2006, nous utiliserions simplement l’opération ordinaire d’intersection d’ensembles et parlerions de R ∩(S×B) ou autre.
Whitehead et Russell ne pouvaient pas faire cela en 1910 parce qu’il manquait une pièce cruciale de la machinerie : la paire ordonnée. En 1910, personne ne savait comment construire une paire ordonnée à partir de la logique et des ensembles. En 2006 (ou même en 1956), nous définirions la paire ordonnée <a, b> comme l’ensemble {{a}, {a, b}}. Puis nous montrerions comme un théorème que <a, b> = <c, d> si et seulement si a=c et b=d, en utilisant les propriétés des ensembles. Puis nous définirions A×B comme l’ensemble de tous les p tels que p = <a,b> ∧ a ∈ A ∧ b∈ B. Puis nous définirions une relation sur les ensemblesA et B comme un sous-ensemble de A×B. Alors nous obtiendrions tout ∗23 et ∗25 et beaucoup de ∗33 et ∗35 et ∗36 gratuitement, et probablement beaucoup d’autres choses aussi.
(Au fait, la chose {{a}, {a, b}} a été inventée par Kuratowski. Elle est généralement attribuée à Norbert Wiener, mais l’idée de Wiener, bien que similaire, était en fait plus compliquée.)
Il n’y a pas de paires ordonnées dans Principia Mathematica,sauf implicitement. Il n’y a même pratiquement pas d’ensembles. Whitehead etRussell veulent tout baser sur la logique. Pour Whitehead et Russell, la notion fondamentale est la « fonction propositionnelle », qui est une fonction φ dont la sortie est une valeur de vérité. Pour chaque fonction de ce type, il existe un ensemble correspondant, qu’ils désignent par !!\hat x\phi(x) !!, l’ensemble de tous les x tels que φ(x) est vrai. Pour Whitehead et Russell, l’arelation est impliquée par une fonction propositionnelle de deux variables, de manière analogue à la manière dont un ensemble est impliqué par une fonction propositionnelle d’une variable. En 2006, nous nous passons des « fonctions de deux variables », et parlons simplement de fonctions dont l’argument (unique) est une paire ordonnée ; une relation devient alors l’ensemble de toutes les paires ordonnées pour lesquelles une fonction est vraie.
Russell est censé avoir dit que la découverte du trait de Shefferstroke (un opérateur logique unique à partir duquel tous les autres opérateurs logiques peuvent être construits) était une avancée considérable, et allait tout changer. Cela nous semble étrange aujourd’hui, car la découverte du trait de Sheffer semble si simple, et ne change pas grand-chose. Il suffit d’ajouter une note au début du chapitre 1 qui dit que ∼p et p∨q sont des abréviations de p|p et p|p.|.q|q, respectivement, de prouver les cinq axiomes fondamentaux et de laisser tout le reste inchangé. Mais Russell aurait pu, avec une certaine justice, dire la même chose de la découverte que les paires ordonnées peuvent être interprétées comme des ensembles, une simple découverte qui aurait vraiment transformé les Principia Mathematica en un travail tout à fait différent.
En tout cas, avec ce contexte en place, nous pouvons discuter de la preuve de 1+1=2 dans les Principia Mathematica. Cela se produit tout à fait tard dans Principia Mathematica, dans la section ∗102. Ma version abrégée ne va que jusqu’à ∗56, mais c’est assez loin pour arriver à l’important théorème précurseur, ∗54.43, scanné ci-dessous :
La notation peut être écrasante, alors concentrons-nous juste sur l’énoncé du théorème, ignorons tout le reste, même la remarque utile en bas :
C’est le théorème qui est prouvé ; ce qui suit est la preuve.
Je dois maintenant expliquer la notation, qui a quelque peu changé depuis 1910. Tout d’abord, Principia Mathematica utilise la notation « points » de Peano pour désambiguïser la préséance, où nous utilisons maintenant des parenthèses à la place. Il faut un peu de temps pour s’habituer à la notation par points, mais elle présente des avantages certains par rapport aux parenthèses. L’idée est simplement d’indiquer le regroupement en mettant des points, de sorte que (1+2)×(3+4)×(5+6) s’écrit1+2.×.3+4.×.5+6. La sous-formule du milieu est entre deux points. La sous-formule (1+2) est entre une paire de points également, mais le point à l’extrémité gauche est superflu, et on l’omet ; de même, la sous-formule (5+6) est délimitée par un point à gauche et par la fin de la formule à droite.
Et si on a besoin d’imbriquer des parenthèses ? Dans ce cas, vous utilisez d’autres points. Un double point ( 🙂 est comme un point simple, mais plus fort. Par exemple, nous écrivons ((1+2)×3)+4 comme 1+2 . × 3 : + 4, et le double point isole l’ensemble de l’expression 1+2 . × 3 en une seule sous-formule à laquelle s’applique le +4.
Parfois, vous avez besoin de plus de niveaux de préséance, et alors vous utilisez des points triples (. : et :.) et quadruples (: :). Cette formule, comme vous le voyez, comporte des points doubles et triples. En traduisant les points en notation standard de la parenthèse, on obtient 54,43 $. \vdash ((\alpha, \beta \in 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \in 2)))$$. L’apparence de cette version est un peu plus encombrée que celle de la version avec les points, et dans le cas de formules complexes, on peut avoir du mal à déterminer quelles parenthèses correspondent à quelles autres. Avec les points, c’est toujours facile. Je pense donc qu’il est un peu regrettable que cette convention soit tombée en désuétude.
Le symbole !\vdash ! n’a pas changé ; il signifie que la formule à laquelle il s’applique est affirmée vraie. !\supset !! est une implication logique, et !\equiv!est une équivalence logique. Λ est l’ensemble vide, que l’on écrit aujourd’hui ∅. ∩ ∪ et ∈ ont leurs significations modernes : ∩ et ∪ sont les opérateurs d’intersection et d’union d’ensembles, et x∈y signifie que x est un élément de l’ensemble y.
Les points restants sont sémantiques. α et β sont des ensembles. 1désigne l’ensemble de tous les ensembles qui ont exactement un élément. C’est-à-dire que c’est l’ensemble { c : il existe a tel que c = {a } }. Les théorèmes sur 1 comprennent, par exemple :
- que Λ∉1 (∗52.21),
- que si α∈1 alors il existe un certain x tel que α ={x}. (∗52.1), et
- que {x}∈1 (∗52.22).
2 est de même l’ensemble de tous les ensembles qui ont exactement deux éléments. Un théorème important sur 2 est ∗54.3, qui dit $$\ast54.3. \vdash 2 = \hat\alpha\{ (\existe x) \> .\>x\in\alpha \> . \3977> \alpha – \iota`x\in 1 \}.$$Dans la notation de Princessia Mathematica, {x}, l’ensemble qui contient x et rien d’autre, s’écrit ι’x, donc ce théorème dit que 2 est identique à l’ensemble de tous les α tels queα a un certain élément x , qui, lorsqu’il est retiré de α, laisse un ensemble à 1 élément.
Voici donc encore le théorème ∗54.43:
Il affirme que si les ensembles α et β ont chacun exactement unélément, alors ils sont disjoints (c’est-à-dire n’ont pas d’éléments en commun) si et seulement si leur union a exactement deux éléments.
La preuve, qui apparaît dans le scan ci-dessus après le mot « Dem. »(abréviation de « démonstration ») va comme suit :
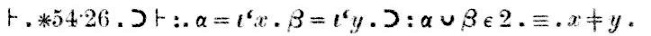
« Le théorème ∗54.26implique que si α = {x} et β = {y}, alorsα∪β a 2 éléments si et seulement si x est différent de y. »
« Par le théorème ∗51.231, ce dernier élément (x est différent dey) est vrai si et seulement si {x} et {y} sontdisjoints. »
« Par ∗13.12, ce dernier bit ({x} et {y} sont disjoints) est vrai si et seulement si α et β eux-mêmes sont disjoints. » La conclusion partielle à ce point,qui est étiquetée (1), est que si α = {x} et β ={y}, alors α∪β ∈ 2 si et seulement siα∩β = Λ.
La preuve se poursuit : « La conclusion (1), avec les théorèmes ∗11.11 et ∗11.35,implique que s’il existe x et y pour que α soit{x} et β soit {y}, alors α∪β ∈ 2si et seulement si α et β sont disjoints. » Cette conclusion est étiquetée (2).
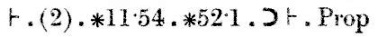
Enfin, la conclusion (2), ainsi que les théorèmes ∗11.54 et ∗52.1,implique le théorème que nous cherchions à prouver.
Ce qu’il faut peut-être remarquer ici, c’est que les pas sont très petits.∗54.26, dont ce théorème dépend fortement, est presque le même ; il affirme que {x}∪{y} ∈ 2 si et seulement si x≠y. ∗54.26, à son tour, dépend de ∗54.101, qui ditque α a 2 éléments si et seulement s’il existe x ety, pas les mêmes, tels que α = {x} ∪{y}. ∗54.101 est juste un tout petit peu différent de la définition de 2. Le théorème ∗51.231 dit que {x} et {y} sontdisjoints si et seulement si x et y sont différents.∗52.1 est une propriété de base de 1 ; nous l’avons vu précédemment.
Les autres théorèmes cités dans la démonstration sont de toutes petites questions techniques. ∗11.54 dit qu’on peut prendre une assertion que deux choses existent et la séparer en deux assertions, chacune affirmant qu’une des choses existe. ∗11.11 est encore plus mince : elle dit que si φ(x, y) est toujours vrai, alors vous pouvez attacher un quantificateur universel, et affirmer que φ(x, y) est vrai pour tous les x et y. ∗13.12 concerne la substitution d’égaux par des égaux : si x et y sont identiques, alors x possède une propriété ψ si et seulement si y le fait aussi.
Je n’ai pas vu les dernières parties des Principia Mathematica, parce que ma copie s’arrête après la section ∗56, et que les trucs arithmétiques sont beaucoup plus tardifs. Mais ce théorème a clairement le sens de 1+1=2 en lui, et le théorème ultérieur (∗110.643)qui affirme réellement 1+1=2 dépend fortement de celui-ci.
Bien que je ne sois pas complètement sûr de ce qui va se passer plus tard(j’ai déjà perdu beaucoup trop de temps sur ce sujet pour en mettre encore plus pour obtenir la version complète de la bibliothèque), je peux faire une supposition éclairée. Principia Mathematica va définir le nombre 17 comme étant l’ensemble de tous les ensembles à 17 éléments, et de même pour tous les autres nombres ; l’utilisation du symbole 2 pour représenter l’ensemble de tous les ensembles à 2 éléments préfigure cela. Ces ensembles de tous les ensembles d’une certaine taille seront alors identifiés comme les « nombres cardinaux ».
Les Principia Mathematica définiront la somme des nombres cardinaux p et qde la manière suivante : prendre un ensemble représentatif a de p;a a a p éléments. Prenons un ensemble représentatif bde q ; b a q éléments. Soit c =a∪b. Si c est un membre d’un certain nombre cardinal r, et si a et b sont disjoints, alors la somme de p et q est r.
Avec cette définition, vous pouvez prouver les propriétés souhaitables habituelles de l’addition, telles que x + 0 = x, x + y = y + x, et 1 + 1 = 2.
En particulier, 1+1=2 découle directement du théorème ∗54.43 ; c’est exactement ce que nous voulons, car pour calculer 1+1, il faut trouver deux représentants disjoints de 1, et prendre leur union ; ∗54.43 affirme que l’union doit être un élément de 2, quels que soient les représentants que nous choisissons, de sorte que 1+1=2.
Post scriptum : Peter Norvig dit que le circonflexe dans la notationPrincipia Mathematica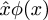 
est la source ultime de l’utilisation du motlambda pour désigner une fonction anonyme dans les langages de programmation Lisp et Python. Je suis sûr que vous savez que ces langages obtiennent « lambda » de l’utilisation de la lettre grecque λ par Alonzo Church pour représenter l’abstraction des fonctions dans son « λ-calcul » : En Lisp,(lambda (u) B) est une fonction qui prend un argumentu et renvoie la valeur de B ; dans le λ-calcul,λu.B est une fonction qui prend un argumentu et renvoie la valeur de B. Norvig dit que Church avait initialement prévu d’écrire la fonctionλu.B comme û.B, mais son imprimante ne pouvait pas faire les accents circonflexes. Il a donc envisagé de déplacer l’accent circonflexe vers la gauche et d’utiliser un lambda en majuscule à la place:Λu.B. La majuscule Λ ressemblait trop àelogique et ∧, ce qui était déroutant, il a donc utilisé la minuscule lambdaλ à la place.
Post post scriptum : Tout le monde dit toujours « Russell et Whitehead ».Les résultats de Google pour « Russell et Whitehead » sont deux fois plus nombreux que ceux pour « Whitehead et Russell », par exemple. Pourquoi ? La couverture et la page de titre disent « Alfred North Whitehead et Bertrand Russell,F.R.S. ». Comment et quand Whitehead a-t-il perdu sa place en tête de liste ?
lien permanent
.