- Objectifs d’apprentissage
- Filets
- Exemple 1
- Exemple 2
- Exercices de révision
- Réponses
- Prismes
- Surface d’un prisme à l’aide de filets
- Exemple 3
- Exercices de révision
- Réponses
- Cylindres
- Surface d’un cylindre à l’aide de filets
- Exemple 4
- Surface d’un cylindre à l’aide d’une formule
- Exemple 5
- Exemple 6
- Exemple 7
- Sphères
- Aire de surface d’une sphère
- Exemple 8
- Exemple 9
- Exercices de révision
- Réponses
Objectifs d’apprentissage
- Comprendre les réseaux.
- Utiliser des réseaux pour représenter des prismes.
- Trouver la surface d’un prisme.
- Trouver la surface des cylindres.
- Trouver la surface d’une sphère.
Filets
Une dernière façon de représenter un solide est d’utiliser un filet. Si vous découpez un filet, vous pouvez le plier pour en faire le modèle d’une figure. Les filets peuvent également être utilisés pour analyser un seul solide. Voici un exemple de filet pour un cube.
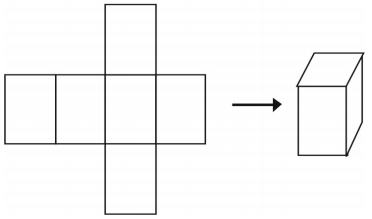
Il y a plus d’une façon de faire un filet pour une seule figure.
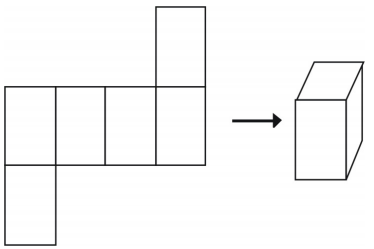
Cependant, tous les arrangements ne créeront pas un cube.
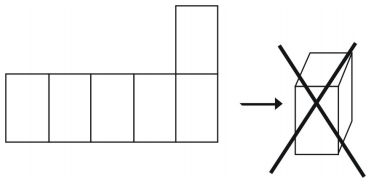
Exemple 1
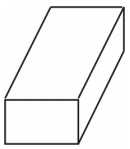
Quel type de figure le filet crée-t-il ? Dessinez la figure.
Le filet crée un prisme rectangulaire en forme de boîte comme indiqué ci-dessous.
Exemple 2
Quel type de filet pouvez-vous dessiner pour représenter la figure représentée ? Dessinez le filet.
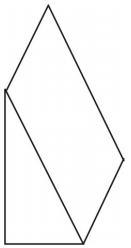
Un filet pour le prisme est montré. D’autres filets sont possibles.
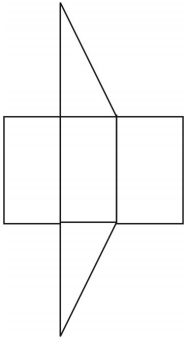
Exercices de révision
Dessinez un filet pour chacun des éléments suivants :
Réponses
Prismes
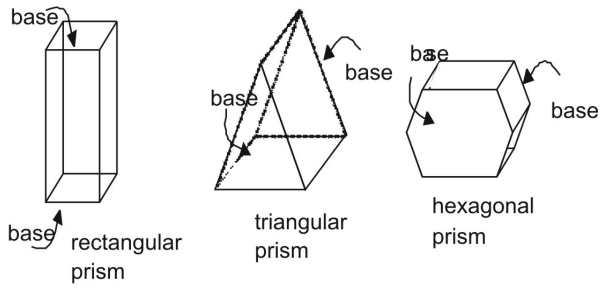
Un prisme est une figure tridimensionnelle avec une paire d’extrémités parallèles et congrues, ou bases. Les côtés d’un prisme sont des parallélogrammes. Les prismes sont identifiés par leurs bases.
Surface d’un prisme à l’aide de filets
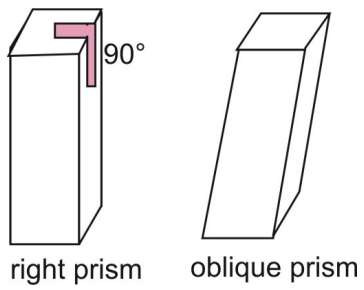
Les prismes ci-dessus sont des prismes droits. Dans un prisme droit, les côtés latéraux sont perpendiculaires aux bases du prisme. Comparez un prisme droit à un prisme oblique, dans lequel les côtés et les bases ne sont pas perpendiculaires.
Deux postulats qui s’appliquent à l’aire sont le postulat de congruence d’aire et le postulat d’addition d’aire.
Vous pouvez utiliser un filet et le postulat d’addition des aires pour trouver l’aire d’un prisme droit.
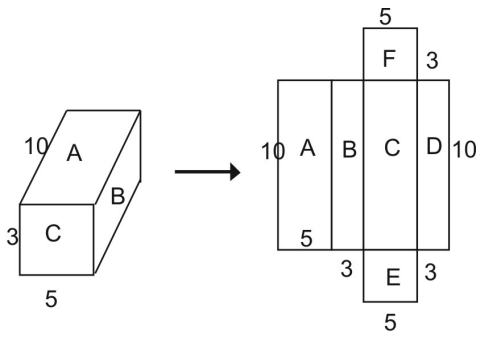
À partir du filet, vous pouvez voir que que l’aire de la surface du prisme entier est égale à la somme des figures qui composent le filet :
Aire de la surface totale = aire A + aire B + aire C + aire D + aire E + aire F
En utilisant la formule de l’aire d’un rectangle, vous pouvez voir que l’aire du rectangle A est :
A = l – w
A = 10 – 5 = 50 unités carrées
De même, les aires des autres rectangles sont réinsérées dans l’équation ci-dessus.
Superficie totale = superficie A + superficie B + superficie C + superficie D + superficie E + superficie F
Superficie totale = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3)
Surface totale = 50 + 30 + 50 + 30 + 15 + 15
Surface totale = 190 unités carrées
Exemple 3
Utiliser un filet pour trouver la surface du prisme.
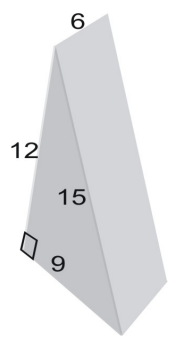
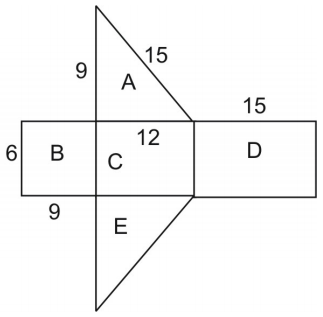
L’aire du filet est égale à l’aire de la figure. Pour trouver l’aire du triangle, on utilise la formule :
\displaystyle{A}=\frac{1}{2}hb\\\ où h est la hauteur du triangle et b sa base.
Notez que les triangles A et E sont congrus donc on peut multiplier l’aire du triangle A par 2.
\displaystyle\text{area}=\text{area }A+\text{area }B+\text{area }C+\text{area }D+\text{area }E\
\displaystyle\text{ }=2(\text{area }A)+\text{area }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\
Thus, la surface est de 324 unités carrées.
Exercices de révision
Pour chacun des cas suivants, trouver la surface sont a en utilisant la méthode des filets et le périmètre


- La base d’un prisme est un triangle rectangle dont les branches sont 3 et 4 et montrent une hauteur de 20. Quelle est la surface totale du prisme?
- Un prisme hexagonal droit a une hauteur de 24 pouces et a des bases qui sont des hexagones réguliers mesurant 8 pouces sur un côté. Quelle est sa surface totale ?
- Quel est le volume du prisme du problème n°4 ?
Dans les questions suivantes, une grange a la forme d’un prisme pentagonal dont les dimensions sont indiquées en pieds :

- Combien de pieds carrés (sans compter le toit) y a-t-il sur la surface de la grange à peindre ?
- Si un gallon de peinture couvre 250 pieds carrés, combien de gallons de peinture sont nécessaires pour peindre la grange ?
- Une boîte en carton est un cube parfait dont le bord mesure 17 pouces. Combien de pieds cubes peut-elle contenir ?
- Une piscine mesure 16 pieds de large, 32 pieds de long et a une profondeur uniforme de 4 pieds. Combien de pieds cubes d’eau peut-elle contenir ?
- Une boîte de céréales a une longueur de 25 cm, une largeur de 9 cm et une hauteur de 30 cm. Combien de céréales peut-elle contenir ?
Réponses
Filets et périmètre :
- 40,5 in2
- 838 cm2
- 252 unités carrées
- 1484.6 unités carrées
- 3990,7 pouces cubes
La grange:
- 2450 pieds carrés
- 10 gallons de peinture
- 2,85 pieds cubes (attention ici. Les unités dans le problème sont données en pouces mais la question demande des pieds.)
- 2048 pieds cubes
- 6750 cm3
Cylindres
Un cylindre est une figure tridimensionnelle avec une paire d’extrémités circulaires parallèles et congruentes, ou bases. Un cylindre a un seul côté incurvé qui forme un rectangle lorsqu’il est posé à plat.
Comme pour les prismes, les cylindres peuvent être droits ou obliques. Le côté d’un cylindre droit est perpendiculaire à ses bases circulaires. Le côté d’un cylindre oblique n’est pas perpendiculaire à ses bases.
Surface d’un cylindre à l’aide de filets
Vous pouvez déconstruire un cylindre en un filet.
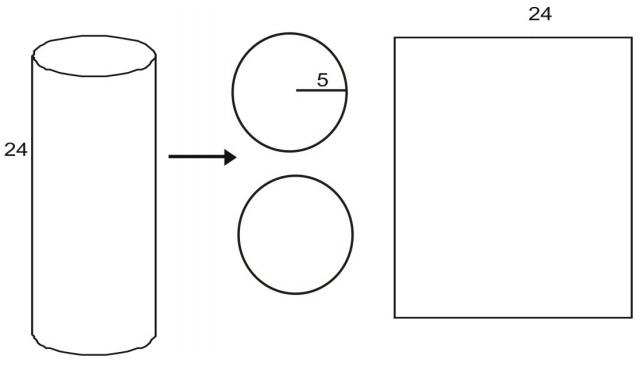
L’aire de chaque base est donnée par l’aire d’un cercle :
A=\pi{r}^2\\
A=\pi(5)^2\
A=25\pi\\
A\approx(25)(3,14)=78,5\
L’aire de la surface latérale rectangulaire L est donnée par le produit d’une largeur et d’une hauteur. La hauteur est donnée par 24. Vous pouvez voir que la largeur de l’aire est égale à la circonférence de la base circulaire.
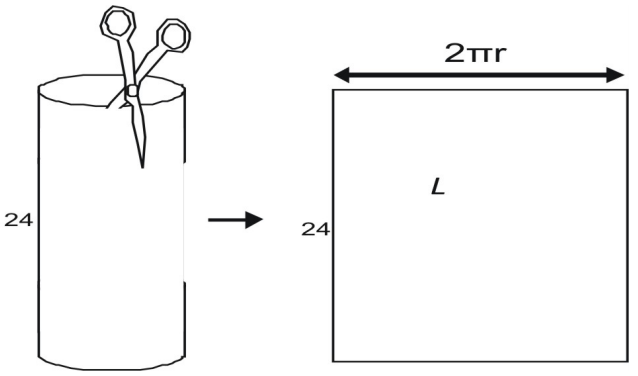
Pour trouver la largeur, imaginez que vous démontez un cylindre en forme de boîte de conserve avec des ciseaux. Lorsque vous coupez la surface latérale, vous voyez qu’elle est égale à la circonférence du sommet de la canette. La circonférence d’un cercle est donnée par C = 2πr, la surface latérale, L, est
L=2{\pi}rh\\
L=2{\pi}(5)(24)\
L=240\pi\\\
L\approx(240)(3.14)=753,6\\\N
Nous pouvons maintenant trouver l’aire du cylindre entier en utilisant A = (aire des deux bases) + (aire du côté latéral).
A=2(75,36)+753,6\\\
A=904,32\\
Vous pouvez voir que la formule que nous avons utilisée pour trouver la surface totale peut être utilisée pour n’importe quel cylindre droit.
Exemple 4
Utilisez un filet pour trouver la surface du cylindre.
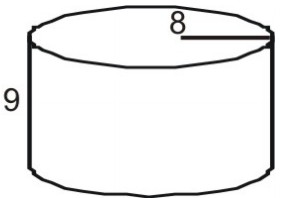
D’abord dessiner et étiqueter un filet pour la figure.
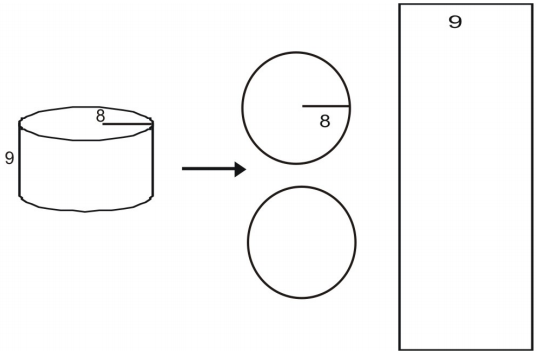
Calculer l’aire de chaque base.
A=\pi{r}^2\
A=\pi(8)^2\\
A=64\pi\\
A\approx(64)(3.14)=200.96\\
Calculate L.
L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16\
Trouve l’aire du cylindre entier.
A=2(200.96)+452.16\
A=854.08\\\N
Ainsi, la surface totale est d’environ 854,08 unités carrées
Surface d’un cylindre à l’aide d’une formule
Vous avez vu comment utiliser les filets pour trouver la surface totale d’un cylindre. Le postulat peut être décomposé pour créer une formule générale pour tous les cylindres droits.
A = 2B + L

Notez que la base, B, de tout cylindre est : B = πr2
L’aire latérale, L, pour tout cylindre est :
L=\text{largeur de la surface latérale}\cdot\text{hauteur du cylindre}\
L=\text{circonférence de la base}\cdot\text{hauteur du cylindre}\\
L=2\pi{r}\cdot{h}\\
En mettant les deux équations ensemble, on obtient :
En soustrayant a de l’équation, on obtient :
L’aire de surface d’un cylindre droit : Un cylindre droit de rayon r et de hauteur h peut être exprimé comme:
A = 2πr2 + 2πrh
ou:
A = 2πr(r + h)
Vous pouvez utiliser les formules pour trouver l’aire de n’importe quel cylindre droit.
Exemple 5
Utiliser la formule pour trouver l’aire du cylindre.
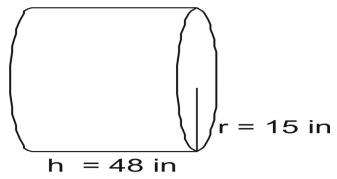
Ecrire la formule et substituer les valeurs et résoudre.
A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\text{pouces carrés}\\
Exemple 6
Trouve la surface du cylindre.
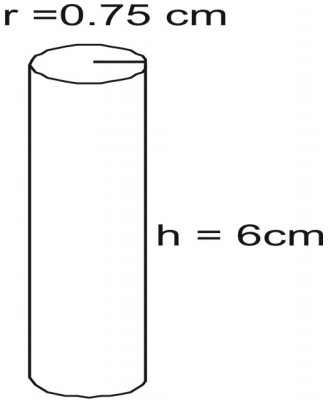
Ecrire la formule et substituer les valeurs et résoudre.
A=2\pi{r}(r+h)\
A=2(3.14)(0.75)\\
A=31.7925\text{pouces carrés}\\
Exemple 7
Trouver la hauteur d’un cylindre qui a un rayon de 4cm et une surface de 226,08 cm2.
Ecrire la formule avec les informations données et résoudre h.
A=2\pi{r}(r+h)\
226,08=2(3,14)(4)\
226,08=25,12\
226,08=100,48+25,12h\\
5=h\
Sphères
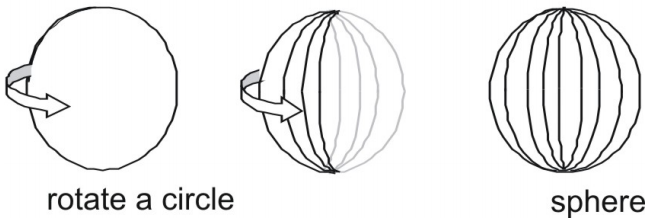
Une sphère est une figure tridimensionnelle qui a la forme d’une balle.

Les sphères peuvent être caractérisées de trois façons.
- Une sphère est l’ensemble de tous les points qui se trouvent à une distance fixe r d’un seul point central O.
- Une sphère est la surface qui résulte de la rotation d’un cercle autour de l’un de ses diamètres.
Aire de surface d’une sphère
On peut déduire la formule de l’aire de surface d’une sphère en prenant des mesures de sphères et de cylindres. Ici, nous montrons une sphère avec un rayon de 3 et un cylindre droit avec à la fois un rayon et une hauteur de 3 et nous exprimons la surface en termes de π.
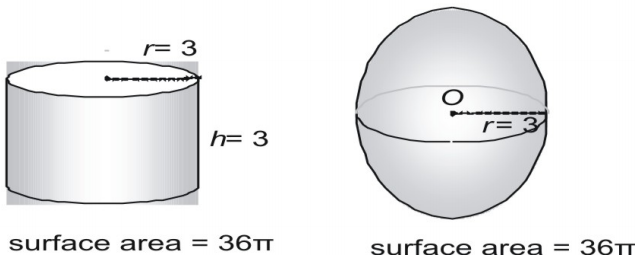
Essayez maintenant une paire plus grande, en exprimant la surface sous forme décimale.
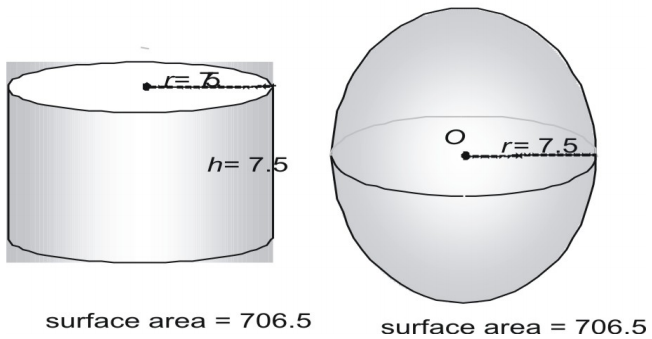
Regardez une troisième paire.
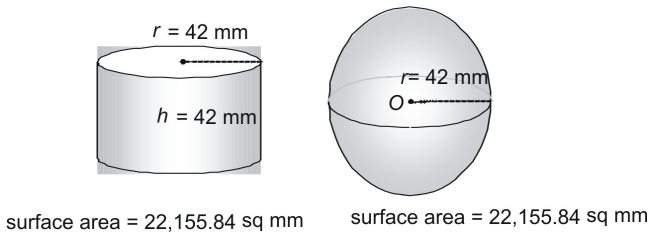
Est-ce une coïncidence qu’une sphère et un cylindre dont le rayon et la hauteur sont égaux au rayon de la sphère aient exactement la même surface ? Pas du tout ! En fait, les Grecs anciens ont utilisé une méthode qui a montré que la formule suivante peut être utilisée pour trouver l’aire de surface de n’importe quelle sphère (ou n’importe quel cylindre dans lequel ).
Exemple 8
Trouver l’aire de la surface d’une sphère avec un rayon de 14 pieds.
Utiliser la formule.
A=4\pi{r}^2\
A=4\pi(14)^2\
A=4\pi(196)\
A=784\pi\\
2461.76\text{ pieds carrés en utilisant }3,14\text{ pour }\pi\
Exemple 9
Déterminez l’aire de la surface de la figure suivante en termes de π.
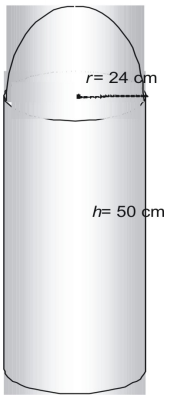
La figure est constituée d’une demi-sphère ou hémisphère, et d’un cylindre sans son sommet.
A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half sphère})=2\pi(576)\
A(\text{demi-sphère})=1152\pi\\text{cm²}\
Trouve maintenant l’aire du cylindre sans son sommet.
A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\
Thus, la surface totale est de 1152\pi+2976\pi=4128\pi\\\
Exercices de révision
- Trouve le rayon de la sphère qui a un volume de 335 cm3.
- Déterminez la surface et le volume de cette forme:

- Le rayon d’une sphère est de 4. Trouvez son volume et sa surface totale.
- Une sphère a un rayon de 5. Un cylindre droit, ayant le même rayon a le même volume. Trouvez la hauteur et la surface totale du cylindre.
- Sphère : volume = 296 cm3. Trouvez le diamètre.
- Sphère : la surface est de 179 in2. Trouvez le rayon.
- Des balles de tennis d’un diamètre de 3,5 pouces sont vendues en boîtes de trois. La boîte est un cylindre. Supposons que les balles touchent la boîte sur les côtés, le haut et le bas. Quel est le volume de l’espace non occupé par les balles de tennis ?
- Une sphère a une surface de 36π in2. Trouvez son volume.
- Une pelle géante, actionnée par une grue, a la forme d’un hémisphère de rayon = 21 pouces. La pelle est remplie d’acier chaud fondu. Lorsque l’acier est versé dans un réservoir de stockage cylindrique dont le rayon est de 28 pouces, l’acier fondu s’élèvera à une hauteur de combien de pouces ?
Réponses
Notez que ces problèmes utilisent π et non 3,14.
- 1. Rayon = 4,31 cm
- Superficie = 706,86 cm2
Volume = 1767,15 cm3 - Volume = 268,08 unités3
Superficie = 201,06 unités2 - Hauteur = 20/3 unités superficie totale = 366,52 unités2
- Diamètre = 8,27cm
- Rayon = 3.77 pouces
- Volume du cylindre = 32.16π in3 volume des balles de tennis = 21.44π in3
Volume de l’espace non occupé par les balles de tennis = 33.68 in3 - Volume = 113.10 in3
- Hauteur de l’acier fondu dans le cylindre sera de 7.88 pouces
.



