Un processus isobare est un processus thermodynamique changement d’état d’une certaine quantité de matière dans lequel la pression reste constante. Ce qu’il peut changer est une ou plusieurs de ses variables d’état. Si la chaleur est transférée au système, un travail est effectué et l’énergie interne du système change également.
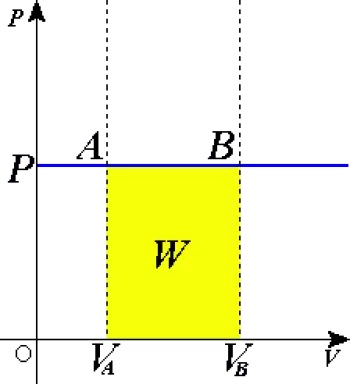
Dans un diagramme pression-volume, il entraîne une ligne horizontale selon la loi des gaz idéaux.
Le processus isobare est régi par la loi de Charles. Selon la loi de Charles, pour une masse fixe de gaz idéal à pression constante, le volume est directement proportionnel à la température de Kelvinte.
Les processus isobares sont régis par la première loi de la thermodynamique. Dans ces processus, l’augmentation de l’énergie est égale à l’augmentation de l’enthalpie moins la pression multipliée par l’augmentation du volume :ΔE = ΔH – P – ΔV.
À ne pas confondre avec les processus isothermes, qui se déroulent à pression constante ou avec les processus adiabatiques, qui n’échangent pas de chaleur. Dans ces processus, une variation de pression peut se produire. Lorsque le processus se fait dans un volume constant, il est appelé processus isochore.
Exemples de processus isobares
Pour mieux comprendre ce processus thermodynamique, il nous sera utile de voir quelques exemples.
-
Phase de détente du cylindre d’un moteur.
-
Faire bouillir de l’eau dans un récipient ouvert.
-
Réchauffement d’un globe sous l’effet du rayonnement solaire.
-
Les ballons à air chaud expérimentent un processus isobare et isochrone.
Réchauffement de l’air d’un ballon
Au début de la matinée, il présente une certaine pression, un certain volume et une certaine température, au fur et à mesure que l’air à l’intérieur se réchauffe, la pression augmente, mais celle-ci ne varie pas en raison de l’augmentation de son volume.
Phase de dilatation du cylindre d’un moteur thermique
Le cylindre d’un moteur thermique peut être dilaté ou contracté selon la phase du cycle. La détente de l’air dans un cylindre à piston mobile auquel on apporte de la chaleur s’effectue par un processus isobare. De même, lors de la compression, le volume est réduit de manière isobare.
Le volume augmentera proportionnellement à sa température et la pression restera constante. Ceci est conforme à la loi de Charles.
Faire bouillir de l’eau dans un récipient ouvert
Un exemple quotidien de processus isobare est l’ébullition de l’eau dans un récipient ouvert. En fournissant de l’énergie thermique à l’eau, celle-ci monte en température et se transforme en vapeur.
La vapeur obtenue a une température plus élevée et occupe un plus grand volume, cependant, la pression reste constante. Dès le début, la pression est égale à la pression atmosphérique.
Chauffage d’une montgolfière
Une montgolfière est un exemple de processus isobare.
Les montgolfières fonctionnent parce que l’air chaud monte. En chauffant l’air à l’intérieur du ballon avec le brûleur, il devient plus léger que l’air plus froid à l’extérieur. Cela fait que le ballon flotte vers le haut, comme s’il était dans l’eau.
La pression à l’intérieur du ballon est la même que celle de l’atmosphère. Lorsque le pilote injecte de la chaleur dans l’air, la température augmente. Elle fait diminue la densité de l’air et à cause de la différence entre sa densité et celle de l’air, le ballon monte.
Thermodynamiquement, une partie de la chaleur est convertie en travail faisant monter la montgolfière. Une partie de cette chaleur est libérée à l’extérieur du système à cause du contact thermodynamique de l’air extérieur et à cause de la perte d’air chaud lors de sa dilatation.
W 1-2 = P ( V 2 – V 1 ) W 1-2 = n R ( T 2 – T 1 ) Q 1-2 = m c p ( T 2 – T 1 ) Q 1-2 = ( k / ( k -1)) P ( V 2 – V 1 )
Où,
-
W 1-2 quantité de travail effectué par le changement d’état
-
Q 1-2 la quantité de chaleur fournie ou retirée
-
P la pression
-
V le volume
-
T la température absolue
-
n la quantité de poussière (généralement exprimée en moles)
-
m la masse de la substance
-
cp la chaleur spécifique de la substance à pression constante
-
k est un rapport égal au quotient de la chaleur spécifique à pression constante et à volume constant, respectivement
.
D’après la première équation, on constate que si le système se dilate (ΔV est positif), alors le système effectue un travail positif. Au contraire, si l’augmentation du volume est négative, le système se contracte et le travail est négatif.
Equation d’état d’un gaz idéal
L’équation d’état d’un gaz idéal (parfois l’équation de Mendeleïev – Clapeyron ou l’équation de Clapeyron) est une formule qui établit la relation entre la pression, le volume molaire et la température absolue d’un gaz idéal. L’équation est :
pV = nRT
Où,
p – pression,
V- volume du gaz,
n- la quantité de gaz,
R – constante universelle des gaz , R ≈ 8,314 J / (mol⋅K),
T – température thermodynamique, K kelvin.