Sun, 18 Jun 2006
1+1=2
Whitehead és Russell Principia Mathematica című műve híres arról, hogy ezer oldalon keresztül bizonyítja, hogy 1+1=2. Persze rengeteg más dolgot is bizonyít. Ha csak azt akarták volna bebizonyítani, hogy 1+1=2, valószínűleg csak feleannyi helyet foglalt volna el.
A Principia Mathematica egy különös könyv, amelyet érdemes megvizsgálni mind történelmi, mind matematikai szempontból. A mű 1910 körül íródott, és a matematikai logika akkor még gyerekcipőben járt, frissen a Peano és Frege által rajta végzett átalakítások után. A jelölés kissé homályos, mert a matematikai jelölés azóta jelentősen fejlődött. És sok olyan egyszerű technika, amelyet ma már természetesnek veszünk, hiányzik.Mint egy rosszul megírt számítógépes program, a Principia Mathematica nagy része ismétlődő kód, különálló szakaszok, amelyek lényegében ugyanazt mondják, mert a szerzők még nem tanulták meg azokat a technikákat, amelyek lehetővé tennék, hogy ezeket a szakaszokat egybefoglalják.
Például a ∗22. szakasz, “Az osztályok számítása”, a részhalmazok relációjának (∗22.01), valamint a halmazegyesítés és halmazmetszés (∗22.02 és .03), a halmaz komplementjének (∗22.04) és két halmaz különbségének (∗22.05) meghatározásával kezdődik. Ezután bizonyítja a halmazegyesítés és halmazmetszés kommutativitását és asszociativitását (∗22.51, .52, .57 és .7), különböző tulajdonságokat, mint !!\alpha\cap\alpha = \alpha !! (∗22.5) és hasonlók, egészen az olyan tételekig, mint a ∗22.92: !!\alpha\subset\beta \rightarrow \alpha\cup(\beta -\alpha)!!.
A ∗23. szakasz a “Relációk számítása”, és majdnem pontosan ugyanígy kezdődik, a szubrelációs reláció meghatározásával (∗23.01), valamint a relációs unió és metszés műveleteit (∗23.02 és .03), egy reláció komplementjét (∗23.04) és két reláció különbségét (∗23.05). A továbbiakban bizonyítja a relációs egyesítés és metszés kommutativitását és asszociativitását (∗23.51, .52, .57 és .7), különböző tulajdonságokat, mint !!\alfa\dot\cap\alfa = \alfa! (∗22.5) és hasonlók, egészen az olyan tételekig, mint az ∗23.92: !!\alpha\dot\subset\beta \rightarrow \alpha\dot\cup(\beta \dot-\alpha)!!.
A ∗24. szakasz a halmazok létezéséről szól, a nullhalmazról !!\Lambda!!, az univerzális halmazról !!{\rm V}!!!, ezek tulajdonságairól, és így tovább, majd a ∗24. szakasz megismétlődik a ∗25-ben egy sor tételben a relációk létezéséről, a null relációról !!\dot\Lambda!!, az univerzális relációról !!\dot {\rm V}!!, ezek tulajdonságairól, és így tovább.
Így csinálta Whitehead és Russell 1910-ben. Hogyan csinálnánk ma? Az S és T közötti reláció azS × T részhalmazaként definiált, tehát halmaz. Az unió, metszés, különbség és a többi művelet pontosan ugyanazok a relációkra, mint a halmazokra, mert a relációk halmazok. A relációk uniójáról és metszéspontjáról szóló tételek, mint például a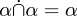 
, egyszerűen eltűnnek, mert ezeket már bizonyítottuk halmazokra, és a relációk halmazok. A nullreláció a nullhalmaz. Az univerzális reláció az univerzális halmaz.
Egy hatalmas mennyiségű más gépezet is eltűnik 2006-ban, a relációk és halmazok egyesítése miatt. A Principia Mathematica speciális jelölést és speciális definíciót igényel a relációnak azokra a párokra való korlátozásának eredményére, amelyek első eleme egy adott S halmaz tagja, vagy amelyek második eleme S tagja, vagy amelyek mindkét eleme S tagja; 2006-ban csak a közönséges halmazmetszési műveletet használnánk, és R ∩(S×B) vagy bármi másról beszélnénk.
Whitehead és Russell 1910-ben nem tudta ezt megtenni, mert hiányzott egy döntő fontosságú gépezet: a rendezett pár. 1910-ben még senki sem tudta, hogyan lehet rendezett párt építeni pusztán logikából és halmazokból. 2006-ban (vagy akár1956-ban) a <a, b> rendezett párt a {{a}, {a, b}} halmazként definiálnánk. Ezután a halmazok tulajdonságait felhasználva tételként megmutatnánk, hogy <a, b> = <c, d>ha és csak akkor, ha a=c és b=d. Ezután definiálnánk A×B-t az összes p olyan halmazaként, hogy p = <a,b> ∧ a ∈ A ∧ b∈ B. Ezután definiálnánk egy relációt azA és B halmazokon, mint A×B részhalmazát. Akkor megkapnánk az összes ∗23 és ∗25 és egy csomó ∗33 és ∗35 és ∗36-ot ingyen, és valószínűleg egy csomó más dolgot is.
(Egyébként a {{a}, {a, b}} dolgot Kuratowski találta ki. Általában Norbert Wiener-nek tulajdonítják, de Wiener ötlete, bár hasonló, valójában bonyolultabb volt.)
A Principia Mathematica-ban nincsenek rendezett párok,csak implicit módon. Még halmazok is alig vannak. Whitehead és Russell mindent a logikára akar alapozni. Whitehead és Russell számára az alapvető fogalom az “állítmányi függvény”, amely egy φ függvény, amelynek kimenete egy igazságérték. Minden ilyen függvénynek van egy megfelelő halmaza, amelyet ők !!\hat x\phi(x)!!!-val jelölnek, az összes olyan x halmaza, amelynél φ(x) igaz. Whitehead és Russell számára az arelációt egy két változóból álló kijelentő függvény implikálja, analóg módon, mint ahogyan egy halmaz implikálódik egy egyváltozós kijelentő függvényből. 2006-ban eltekintünk a “kétváltozós függvényektől”, és csak olyan függvényekről beszélünk, amelyeknek (egyetlen) argumentuma egy rendezett pár; a reláció ekkor azon rendezett párok halmaza lesz, amelyekre a függvény igaz.
Russell állítólag azt mondta, hogy a Sheff-ütés (egyetlen logikai operátor, amelyből az összes többi logikai operátor felépíthető) felfedezése óriási előrelépés volt, és mindent meg fog változtatni. Ez ma már furcsának tűnik számunkra, mert a Sheffer-ütés felfedezése olyan egyszerűnek tűnik, és valójában semmi fontosat nem változtat. Csak egy megjegyzést kell az 1. fejezet elejéhez csatolni, amely szerint ∼p és p∨q a p|p, illetve p|p.|.q|q rövidítése, bizonyítani az öt alapaxiómát, és minden mást változatlanul hagyni. De Russell joggal mondhatta volna ugyanezt arról a felfedezésről, hogy a rendezett párokat halmazokként lehet értelmezni, egy egyszerű felfedezésről, amely a Principia Mathematica-t valóban egy egészen más művé változtatta volna.
Mindenesetre, ezzel a háttérrel a helyén, megvitathatjuk a Principia Mathematica 1+1=2 bizonyítását. Ez a Principia Mathematica-ban elég későn, a ∗102. szakaszban történik. Az én rövidített változatom csak az ∗56-ig tart, de ez elég messze van ahhoz, hogy eljussunk a fontos előzménytételhez, az ∗54.43-hoz, amelyet alább szkennelünk:
A jelölés túlterhelő lehet, ezért koncentráljunk csak a tétel kifejtésére, és hagyjunk figyelmen kívül minden mást, még az alján lévő hasznos megjegyzést is:
Ez a tétel, amit bizonyítunk; ami ezután következik, az a bizonyítás.
Most meg kell magyaráznom a jelölést, ami1910 óta némileg megváltozott. Először is, a Principia Mathematica a Peano-féle “pontok” jelölést használja az elsőbbség megkülönböztetésére, ahol mi most zárójeleket használunk helyette. A pont jelölés némi megszokást igényel, de van néhány határozott előnye a zárójelekkel szemben. Az ötlet lényege, hogy a csoportosítást pontok elhelyezésével jelezzük, így az (1+2)×(3+4)×(5+6) a következőképpen írható: 1+2.×.×.3+4.×.5+6. A középső részformula egy pairof pont között van. Az (1+2) alformula szintén pontpár között van, de a bal oldali pont felesleges, és kihagyjuk; hasonlóképpen az (5+6) alformulát a bal oldalon egy pont, a jobb oldalon pedig a képlet vége határolja.
Mi van, ha zárójeleket kell beillesztenünk? Akkor több pontot használsz. A dupla pont (:) olyan, mint az egyszerű pont, de erősebb. Például a ((1+2)×3)+4-et 1+2-ként írjuk. × 3 : + 4, és a dupla pont elkülöníti az egész 1+2 . × 3 kifejezést egyetlen részformulává, amelyre a +4 vonatkozik.
Néha több elsőbbségi szintre van szükség, és akkor háromszoros (.: és :.) és négyszeres (::) pontokat használunk. Ez a képlet, mint látod, tartalmazdupla és tripla pontokat. Ha a pontokat lefordítjuk a standardparenthesis jelölésbe, akkor $$$\ast54.43. \vdash ((\alpha, \beta \in 1 ) \supset (( \alpha\cap\beta = \Lambda) \equiv (\alpha\cup\beta \in 2)))$$$. Ez meglehetősen áttekinthetetlenebbül néz ki, mint a pontokkal ellátott változat, és a bonyolult képleteknél gondot okozhat kitalálni, hogy melyik zárójel melyikhez illik. A pontokkal ez mindig könnyű. Szóval szerintem egy kicsit szerencsétlen, hogy ez a konvenció kiesett a használatból.
A !!\vdash!! szimbólum nem változott; ez azt jelenti, hogy a formula, amelyre vonatkozik, igaznak bizonyul. !!\supset!! a logikai implikáció, és!!\equiv!! a logikai ekvivalencia. Λ az üres halmaz, amit manapság ∅-nak írunk. ∩ ∪ ∩ és ∈ modern jelentéseik vannak: ∩ és ∪ a halmazmetszés és az unióoperátorok, és x∈y azt jelenti, hogy x az y halmaz eleme.
A többi pont szemantikai. α és β halmazok. 1azoknak a halmazoknak a halmazát jelöli, amelyeknek pontosan egy eleme van. Vagyis ez a { c : létezik olyan a, hogy c = {a } }. Az 1-re vonatkozó tételek közé tartozik például:
- hogy Λ∉1 (∗52.21),
- hogy ha α∈1 akkor van olyan x, hogy α ={x} (∗52.1), és
- hogy {x}∈1 (∗52.22).
2 hasonlóképpen azoknak a halmazoknak a halmaza, amelyeknek pontosan két eleme van. A 2-vel kapcsolatos fontos tétel az ∗54.3, amely azt mondja, hogy $$$\ast54.3. \vdash 2 = \hat\alpha\{ (\ létezik x) \> .\>x\in\alpha \> . \> \alpha – \iota`x\in 1 \}.$$$A Principia Mathematica jelölésében az {x}, az x-et és semmi mást nem tartalmazó halmazt ι’x-nek írjuk, így ez a tétel azt mondja, hogy 2 azonos az összes α olyan halmazával, hogyα-nak van valamilyen x eleme, amely, ha eltávolítjuk α-ból,1 elemű halmazt hagy.
Íme tehát ismét az ∗54.43 tétel:
Ez azt állítja, hogy ha α és β halmazok mindegyike pontosan egyelemű, akkor diszjunktek (azaz nincs közös elemük), ha és csak akkor, ha uniójuknak pontosan két eleme van.
A bizonyítás, amely a fenti beolvasásban a “Dem.” (a “demonstráció” rövidítése) szó után szerepel, így szól:
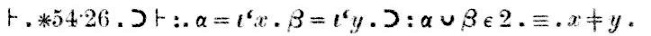
“Az ∗54.26. tétel azt állítja, hogy ha α = {x} és β = {y}, akkorα∪β 2 elemű, ha és csak akkor, ha x különbözik y-tól”.
“Az ∗51.231 tétel szerint ez utóbbi (x különbözik y-tól) akkor és csak akkor igaz, ha {x} és {y} diszjunktek.”
“A ∗13.12 tétel szerint ez az utolsó bit ({x} és {y} diszjunkt) akkor és csak akkor igaz, ha α és β maguk is diszjunktek.” A részleges következtetés ezen a ponton,amelyet (1) jelöl, az, hogy ha α = {x} és β ={y}, akkor α∪β ∈ 2, ha és csak akkor, haα∩β = Λ.
A bizonyítás folytatódik: “Az (1) következtetés az ∗11.11. és ∗11.35. tételekkel együtt azt jelenti, hogy ha létezik x és y úgy, hogy α ={x} és β = {y}, akkor α∪β ∈ 2, ha és csak akkor, ha α és β diszjunktek.” Ezt a következtetést (2) jelöli.
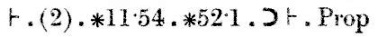
Végül a (2) következtetés a ∗11.54 és ∗52.1 tételekkel együtt implikálja azt a tételt, amit bizonyítani próbáltunk.
Mégis azt kell itt észrevenni, hogy a lépések nagyon kicsik. ∗54.26, amelytől ez a tétel erősen függ, majdnem ugyanez; azt állítja, hogy {x}∪{y} ∈ 2, ha és csak akkor, ha x≠y. Az ∗54.26 viszont az ∗54.101-től függ, amely azt mondja, hogy α-nak akkor és csak akkor van 2 eleme, ha létezik x és y, amelyek nem azonosak, úgy, hogy α = {x} ∪{y}. Az ∗54.101 csak egy icipicit különbözik a 2 definíciójától. Az ∗51.231 tétel azt mondja, hogy {x} és {y} akkor és csak akkor diszjunkt, ha x és y különböző.Az ∗52.1 az 1 alapvető tulajdonsága; ezt már láttuk korábban.
A demonstrációban idézett többi tétel nagyon apró technikai kérdés. A ∗11.54 azt mondja, hogy vehetünk egy olyan állítást, hogy két dolog létezik, és szétválaszthatjuk két állításra, amelyek mindegyike azt állítja, hogy az egyik dolog létezik. A ∗11.11 még karcsúbb: azt mondja, hogy ha φ(x, y) mindig igaz, akkor csatolhatunk egyuniverzális kvantort, és állíthatjuk, hogy φ(x, y) minden x-re és y-ra igaz. A ∗13.12 az egyenlők helyettesítésére vonatkozik: ha x és y azonosak, akkor x akkor és csak akkor rendelkezik egy ψ tulajdonsággal, ha yd is rendelkezik.
A Principia Mathematica későbbi részeit még nem láttam, mert az én példányom az ∗56. szakasz után abbamarad, és az aritmetikai dolgok sokkal később vannak. De ebben a tételben egyértelműen benne van az 1+1=2 értelme, és a későbbi tétel (∗110.643), amely valójában az 1+1=2-t állítja, erősen függ ettől a tételtől.
Bár nem vagyok teljesen biztos benne, hogy mi fog történni később (már így is túl sok időt pazaroltam erre ahhoz, hogy még több időt szánjak a könyvtárból a teljes verzió megszerzésére), tudok egy megalapozott becslést tenni. A Principia Mathematica a 17-es számot úgy fogja definiálni, mint az összes 17 elemű halmaz halmaz halmazát, és ugyanígy minden más számot; a 2 szimbólum használata az összes 2 elemű halmaz halmaz halmazának jelölésére előre jelzi ezt. A meghatározott méretű halmazok halmazait ezután “kardinális számokként” fogjuk azonosítani.
A Principia Mathematica a p és q kardinális számok összegét valahogy így definiálja: vegyünk egy reprezentatív halmazt p-ből;a-nak p eleme van. Vegyünk egy reprezentatív halmazt bből q; b-nek q eleme van. Legyen c =a∪b. Ha c tagja valamilyen r kardinális számnak, és ha a és b diszjunkt, akkor p és q összege r.
Ezzel a definícióval bizonyítani lehet az összeadás szokásos kívánatos tulajdonságait, például x + 0 = x, x + y = y + x, 1 + 1 = 2.
Különösen az 1+1=2 következik közvetlenül az ∗54.43 tételből; ez pont az, amit akarunk, mert az 1+1 kiszámításához meg kell találnunk 1 két diszjunkt képviselőjét, és az egyesítésüket kell vennünk; az ∗54.43 azt állítja, hogy az egyesítésnek 2 elemének kell lennie, függetlenül attól, hogy melyik képviselőt választjuk, így 1+1=2.
Post scriptum: Peter Norvig azt mondja, hogy a Principia Mathematica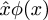 
jelölésében a circumflex 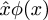a végső forrása annak, hogy a Lisp és Python programozási nyelvekben az anonim függvények jelölésére alambda szót használják. Biztosan tudja, hogy ezek a nyelvek a “lambda” szót a görög λ betű használatából kapták, amelyet Alonzo Church használt a “λ-kalkulusban” a függvényabsztrakció ábrázolására: A Lispben a(lambda (u) B) olyan függvény, amely elfogad egy argumentumot és visszaadja B értékét; a λ-kalkulusban a λu.B olyan függvény, amely elfogad egy argumentumot és visszaadja B értékét. Norvig szerint Church eredetileg azt tervezte, hogy azλu.B függvényt ű.B-nek írja, de a nyomtatója nem tudta a körkörös ékezeteket. Ezért fontolóra vette, hogy a cirkumflexet balra helyezi, és helyette nagybetűs lambdát használ:Λu.B. A nagybetűs Λ túlságosan hasonlított a logikai és a ∧-ra, ami zavaró volt, ezért helyette kisbetűs lambdaλ-t használt.
Post post scriptum: Mindenki mindig azt mondja, hogy “Russell és Whitehead”.A Google találatai például a “Russell és Whitehead”-re kétszeresen meghaladják a “Whitehead és Russell” találatokat. Miért? A borítón és a címlapon az áll: “Alfred North Whitehead and Bertrand Russell,F.R.S.”. Hogyan és mikor veszítette el Whitehead az első helyet?
állandó hivatkozás