Az amortizált elemzés olyan algoritmusoknál használatos, amelyeknek drága műveletei csak ritkán fordulnak elő.

Amortizált komplexitáselemzést leginkább olyan adatstruktúráknál használják, amelyek állapota a műveletek között megmarad.Az alapötlet az, hogy egy drága művelet megváltoztathatja az állapotot úgy, hogy a legrosszabb eset hosszú ideig nem fordulhat elő újra, így amortizálódik a költsége.
Legyen T1, T2, …, Tk egy adatszerkezeten végzett műveletek sorozatának komplexitása. E sorozat egyetlen műveletének amortizált bonyolultsága(T1 + T2 + …+ …+ Tk) / k.
Példa: dinamikus tömb
Egy dinamikus tömbben az elemeket egy mögöttes fix tömb elején tároljuk,a többi pozíció pedig kihasználatlan.
// Append x to the end of a dynamic array a.algorithm append(x, a): if a.size == a.capacity b ← new array with twice the capacity of a copy a into b a ← b a ← x a.size++Itt egy nézet a memóriáról, amikor a 2, 7, 1, 3, 8, 4 elemeket egy kezdetben üres, 2 kapacitású tömbhöz csatoljuk.
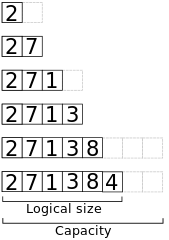
Legrosszabb esetbeli idő
A legrosszabb esetbeli időbonyolultság egy elem hozzáadásához egy n hosszúságú tömbhöz ezzel az algoritmussal Θ(n).Ha a tömb tele van, az algoritmus egy új, 2n hosszúságú tömböt rendel ki,majd a régi tömb elemeit átmásolja az új tömbbe.
Figyelem, ez az eredmény túl pesszimista.A következő n append művelet sokkal olcsóbb lesz – mindegyik állandó idő alatt fog lefutni, mivel az újonnan kiosztott tömbben van hely az összes új elem számára.
Amortizált idő
Az amortizált idő elemzése sokkal jobban megérti az algoritmust.
Megfontoljuk az n append műveletből álló sorozatot,ahol egy 1 hosszúságú tömbtel kezdünk. Egy gondos elemzés megmutatja,hogy ezeknek a műveleteknek a teljes ideje csak Θ(n).
- Összesen n állandó idejű hozzárendelési és növelési művelet lesz.
- Az átméretezés csak az 1, 2, 4, …, 2k műveletnél történik, összesen 1 + 2 + 4 + …+ 2k = 2-2k – 1 állandó idejű elemmásolási művelet. Mivel 2k ≤ n, ez legfeljebb 2n – 1.
Az egyetlen append művelet amortizált időbonyolultsága tehát Θ(1).
Tovább az algoritmus elemzéséről

Az időbonyolultság: Számold a lépéseket

Big O jelölés