A határréteg egy mozgó áramlással érintkező fal szilárd felületéhez közeli vékony viszkózus folyadékréteg, amelyben (δ vastagságán belül) az áramlási sebesség a falnál a nullától (ahol az áramlás a viszkozitása miatt a falhoz “tapad”) a határon Ue-ig változik, ami megközelítőleg (1%-os hibán belül) megfelel a szabad áramlási sebességnek (lásd az 1. ábrát). Szigorúan véve a δ értéke tetszőleges érték, mivel a folyadék és a szilárd test közötti molekuláris kölcsönhatástól függő súrlódási erő a faltól való távolsággal csökken, és a végtelenben nullával lesz egyenlő.
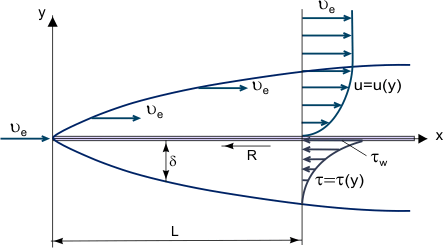
1. ábra. Határréteg növekedése egy sík lemezen.
A határréteg alapvető fogalmát L. Prandtl (1904) javasolta, a határréteget nagyon nagy Reynolds-számú Re, azaz a tehetetlenségi erőkhöz képest viszonylag kis viszkozitású áramlásokban kialakuló folyadékrétegként definiálja. Ez akkor figyelhető meg, ha a testek nagy sebességű légáramlatnak vannak kitéve, vagy ha a testek nagyon nagyok és a légáramlat sebessége mérsékelt. Ebben az esetben egy viszonylag vékony határrétegben a súrlódási nyírófeszültség (viszkózus nyíróerő): τ = η (ahol η a dinamikus viszkozitás; u = u(y) – a határréteg hosszirányú sebességkomponensének “profilja”, lásd az 1. ábrát) nagyon nagy lehet; különösen a falnál, ahol u = 0 és τw = ηw, bár maga a viszkozitás meglehetősen kicsi lehet.
A határrétegen kívüli súrlódási erőket (a tehetetlenségi erőkkel szemben) figyelmen kívül lehet hagyni, és Prandtl koncepciója alapján két áramlási területet lehet figyelembe venni: a határréteget, ahol a súrlódási hatások nagyok, és a majdnem inviscid áramlási magot. Abból kiindulva, hogy a határréteg egy nagyon vékony réteg (δ << L, ahol L az áramlással érintett test vagy az áramlást tartalmazó csatorna jellegzetes lineáris mérete, amelynek vastagsága a Re növekedésével csökken, 1. ábra), a határréteg vastagságának nagyságrendjét a következő összefüggésből becsülhetjük meg:
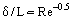
Például, ha egy repülőgép Ue = 400 km/óra sebességgel repül, a határréteg vastagsága a szárny hátulsó élénél 1 méteres akkord (profilhossz) esetén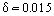 
m. Amint azt kísérletileg megállapították, a test belépő szakaszán lamináris határréteg alakul ki. Fokozatosan, néhány destabilizáló tényező hatására a határréteg instabillá válik, és a határréteg átmenete turbulens áramlási rendszerbe történik. Speciális kísérleti vizsgálatok megállapították a turbulens és a lamináris tartomány közötti átmeneti régió létezését. Bizonyos esetekben (például a külső áramlás magas turbulenciaszintje esetén) a határréteg közvetlenül az áramlás stagnálási pontja után turbulenssé válik. Bizonyos körülmények között, például nagy nyomásesés esetén a gyorsuló turbulens áramlásban egy fordított jelenség, nevezetesen az áramlás relaminarizálódása megy végbe.
A határréteg viszonylagos vékonysága ellenére nagyon fontos az áramlás és a test közötti dinamikus kölcsönhatási folyamatok beindításában. A határréteg határozza meg a repülő jármű aerodinamikai ellenállását és felhajtóerejét, vagy a csatornákban folyó folyadékáramlás energiaveszteségét (ebben az esetben hidrodinamikai határréteg, mert van egy termikus határréteg is, amely a hőátadás termodinamikai kölcsönhatását határozza meg).
A határréteg paramétereinek kiszámítása a viszkózus folyadékmozgásra vonatkozó Navier-Stokes-egyenletekből nyert egyenletek megoldásán alapul, amelyeket először jelentősen egyszerűsítenek, figyelembe véve a határréteg vékonyságát.
A L. Prandtl által javasolt megoldás lényegében a Navier-Stokes-egyenlet hatványsoros bővítésének első tagja, a sorbővítést a dimenziótlan paraméter (δ/L) hatványaira végezzük. A kisebb paraméter ebben a tagban nulla hatványon áll, így a határrétegegyenlet a határrétegegyenlet (nagy Re-nál) aszimptotikus kiterjesztésében (aszimptotikus megoldás) a nulla közelítése.
A Navier-Stokes-egyenlet határréteg-egyenletekre való átalakítása szemléltethető a lamináris határréteg Prandtl-egyenletének levezetésével kétdimenziós, testerők nélküli, összenyomhatatlan áramlásban.
Ebben az esetben a Navier-Stokes-egyenletek rendszere:
Az egyenlet néhány tagjának nagyságrendjének kiértékelése után az Eq. (2) és a kis tagok figyelmen kívül hagyásával a lamináris határrétegre vonatkozó Prandtl-egyenletek rendszere a következő lesz:
melyben x, y a hosszanti és oldalsó koordináták (1. ábra); v a sebességkomponens az “y” tengely mentén; p a nyomás; t az idő; és n a kinematikai viszkozitás.
A határréteg vékony, és az Ue sebesség a külső peremén eléggé és pontosan meghatározható, mint a fal mentén az első közelítésig számított ideális (inviszid) folyadékáramlás sebessége, anélkül, hogy figyelembe vennénk a határrétegnek a külső áramlásra gyakorolt fordított hatását. A (3. egyenletben szereplő hosszirányú nyomásgradiens = (p(y) = const) az ideális folyadék Euler-féle mozgásegyenletéből ábrázolható. A fentiek alapján a Prandtl-egyenleteket véges alakjukban a következőképpen írjuk fel:
Ez egy másodrendű parabolikus, nemlineáris parciális differenciálegyenletek rendszere, amelyet kezdeti és peremfeltételekkel oldunk meg
A (4) egyenletrendszert az u és v sebességkomponensek tényleges értékeire írjuk fel. A turbulens áramlásra kapott egyenletek általánosításához a turbulens áramlás paramétereinek tényleges, átlagolt és pulzáló komponensei közötti jól ismert összefüggést kell használni. Például a sebességkomponensek esetében léteznek olyan összefüggések, amelyek összekötik a tényleges u és v, az átlagos ū és
és a pulzáló u’ és v’ komponenseket:
Néhány átrendezés után a (3) rendszerből egy másik egyenletrendszert kaphatunk, különösen állandósult áramlásra:
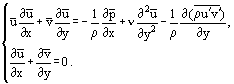
A határrétegben a súrlódási nyírófeszültségre a következő összefüggést használva:
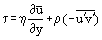
és figyelembe véve, hogy a lamináris határrétegben u = u’ és
a Prandtl-egyenleteket a lamináris és turbulens áramlásra egyaránt érvényes formában lehet átírni:
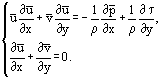
A legegyszerűbb megoldásokat egy vékony lapos lemezen lévő lamináris határrétegre kaptuk kétdimenziós, párhuzamos, összenyomhatatlan folyadék áramlásában (1. ábra). Ebben az esetben az egyenletek feltételei: x ~ L, y ~ δ, δ ~
nagyságrendjének becslése lehetővé teszi, hogy az x és y változókat egy relációban egyesítsük
és a (8) egyenlet megoldását (dp/dx = 0-nál) az u és v új ξ paramétertől való függésének meghatározására redukáljuk. Másrészt az u, v sebességkomponensek és a ψ
áramlási függvény közötti jól ismert összefüggések felhasználásával egy harmadrendű közönséges nemlineáris differenciálegyenletet kaphatunk, (8)
parciális differenciálegyenletek rendszere helyett f(ξ) a ξ változó ismeretlen függvénye: f = ƒ =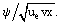
Az egyenlet első numerikus megoldása. (10) egyenletet Blasius (1908) kapta meg a határréteg fizikai feltételeinek megfelelő peremfeltételek mellett y = 0-nál: u = 0, v = 0; y → ∞-nél; u → Ue (Blasius-féle határréteg).
A 2. ábrán a Blasius-féle megoldás eredményeit (folytonos vonal) hasonlítja össze a kísérleti adatokkal. Ezen adatok felhasználásával kiértékelhető a viszkózus határréteg vastagsága. ξ 
2,5 esetén (u/Ue 0,99) (2. ábra); következésképpen a (9. egyenletből kapjuk:
2. ábra.
A Blasius-féle numerikus számításokból az f(ξ) függvény második deriváltjának értéke a falsúrlódási nyírófeszültségnél, az összefüggés ebben az esetben:
Az L hosszúságú lemez mindkét oldalán ható R súrlódási erő (1. ábra) szintén az egyenletből határozható meg. (11) egyenletből:
mint a súrlódási együttható sík lemezekre:
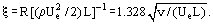
Dacára annak, hogy a Prandtl-egyenletek sokkal egyszerűbbek, mint a Navier-Stokes-egyenletek, megoldásukat csak korlátozott számú problémára kaptuk meg. Sok gyakorlati probléma esetén nem szükséges a határrétegben sebességprofilokat meghatározni, csak a vastagságot és a nyírófeszültséget. Ilyen információkhoz juthatunk az integrál impulzusegyenlet
A (12) integrálösszefüggés mind a lamináris, mind a turbulens határrétegre érvényes.
A (12) egyenletben szereplő integrál alatt olyan függvények állnak, amelyeket a priori nem ismertünk, de amelyek a folyadék paramétereinek eloszlását jellemzik a réteg δ vastagságában. Az integrál kiszámításának hibája pedig kisebb, mint a hozzávetőlegesen feltételezett ρu = ρu(y) integrálfüggvény hibája. Ezek megteremtik a feltételeket a határréteg paramétereinek közelítő számítási módszereinek kifejlesztéséhez, amelyek kevésbé időigényesek, mint a Prandtl-egyenletek integrálásának egzakt módszerei. Az alapvető koncepciót először T. von Karman javasolta, aki bevezette az ilyen tetszőleges rétegvastagságot δ*
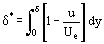
és a lendületeltolódás vastagságát δ**
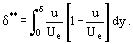
így átalakíthatjuk az egyenletet. (12) egyenletet kétdimenziós inkompresszibilis folyadék határrétegére a következőképpen alakíthatjuk át:
A (15) egyenletben három ismeretlen függvény van, nevezetesen δ* = δ*(x), δ** = δ**(x) és τw = τw(x) .
Az olyan közönséges differenciálegyenlet megoldása, mint az Eq. (15) megoldása általában megköveteli a határréteg vastagságára vonatkozó sebességeloszlás (sebességprofil) feltételezését (vagy ábrázolását) néhány jellemző paraméter (alakparaméter) függvényében, valamint empirikus adatok felhasználását a Cf = 2τw/(ρU2e) súrlódási együttható és a határréteg tetszőleges vastagsága közötti kapcsolatról (súrlódási törvény).
A δ* és δ** értékeit illetően néhány határozott fizikai magyarázat adható. A (13) egyenlet integránsfüggvénye átrendezés után tartalmaz egy (Ue – u) kifejezést, amely a sebességcsökkenést jellemzi. A (14. egyenletben szereplő integrál tehát a határrétegen keresztüli áramlási sebesség csökkenésének mérőszámának tekinthető az Ue sebességű tökéletes folyadékáramláshoz képest. Másrészt a δ* értéke a súrlódási erők hatására a külső áramlási vonalnak a falra merőleges (az “y” tengely mentén) mentén történő eltérésének mértékének tekinthető. A (14) egyenlet integrálszerkezetének e megfontolásából arra következtethetünk, hogy δ** a határrétegben a súrlódási erők hatására bekövetkező impulzuscsökkenést jellemzi.
A következő összefüggések érvényesek:
ahol H a határréteg sebességprofiljának alakparamétere. Például lineáris eloszlás esetén u = ky,
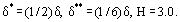
A turbulens határréteg paramétereinek előrejelzésére jelenleg széles körben alkalmaznak úgynevezett fél-empirikus elméleteket. Ebben az esetben feltételezik, hogy a teljes τ súrlódási feszültség a turbulens határrétegben egy összeg
Itt τT a kiegészítő (turbulens vagy Reynolds) súrlódási feszültség, különösen inkompresszibilis áramlásban
lásd egyenletet. (7).
Ez az ábrázolás közvetlenül kapcsolódik a határréteg mozgásegyenletrendszeréhez (6). A kompresszibilis határrétegben a sűrűségpulzációk hőmérsékletpulzációk eredményének tekinthetők
ahol β = (1/T) a térfogattágulási együttható.
A τT meghatározásához további félempirikus hipotéziseket használunk a turbulens impulzusátvitelről. Például,
ahol ηT a J. Boussinesq által 1877-ben bevezetett turbulens viszkozitás dinamikus együtthatója.
A molekuláris és turbulens anyagcsere hasonlóságának fogalma (hasonlóságelmélet) alapján Prandtl bevezette a keveredési hossz (die Mischungsweg) hipotézist. A keveredési hossz 1 az az út, amelyen egy véges folyadékmennyiség (“molekula”) az egyik átlagos mozgású rétegből a másikba jut anélkül, hogy impulzusmomentuma megváltozna. Ennek a feltételnek megfelelően levezetett egy egyenletet, amely alapvetőnek bizonyult a határrétegelmélet számára:
A falközeli áramlás határrétegének turbulens tartományára L. Prandtl az 1 hosszúságot y
val arányosnak tekintette, ahol κ egy empirikus állandó.
A falhoz közel, ahol ηT << η, a viszkózus molekuláris súrlódás a meghatározó tényező. A határréteg ezen részének δ1 vastagsága, amelyet lamináris vagy viszkózus alrétegnek nevezünk,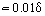 
. Az alrétegen kívül az ηT értéke növekszik, és több nagyságrenddel nagyobb értéket ér el, mint η. Ennek megfelelően a határrétegnek ebben a turbulens magnak nevezett zónájában τT > 0 = η. Néha a turbulens magot felosztják a pufferzónára, ahol a lamináris és a turbulens súrlódás hasonló értékű, és a fejlett zónára, ahol τT >> τ0. Erre a régióra a (18) egyenlet integrálása után és a (19) egyenlet figyelembevételével levezethető a logaritmikus sebességprofilra vonatkozó kifejezés:
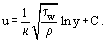
Ha dimenziótlan (vagy univerzális) koordinátákat használunk.
ahol
az úgynevezett dinamikus sebesség (vagy súrlódási sebesség), Eq. (20) a következő formában írható át:
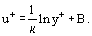
A sebességeloszlás univerzális koordinátákban történő ábrázolásával és a turbulens viszkozitási együttható matematikai modelljeivel részletesebben a Turbulens áramlás fejezetben foglalkozunk.
A turbulens határréteg félempirikus elméletének egyik jelenlegi változatával, amelyet S. S. S. Kutateladze és A. I. Leontiev a turbulens határrétegek úgynevezett aszimptotikus elméletén alapul Re → ∞ esetén, ahol a lamináris (viszkózus) alréteg δ1 vastagsága nagyobb ütemben csökken, mint δ, aminek következtében (δ1/δ) → 0.
Egy ilyen körülmények között “eltűnő viszkozitású” turbulens határréteg alakul ki. Ebben a rétegben η → 0, de nem egyenlő nullával, és ebben a tekintetben a réteg eltér a tökéletes folyadékáramlástól. A S. S. Kutateladze és A. I. Leontiev (1990) által bevezetett relatív súrlódási törvény fogalmát
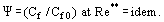
A törvényt a vizsgált állapotra vonatkozó Cf súrlódási együttható és a Cf0 “standard” körülményekre vonatkozó értékének hányadosaként határozzák meg egy sík, át nem eresztő lemezen, amelyet inkompresszibilis, izoterm áramlással körbeáramoltatnak, mindkét együtthatót Re** = Ueδ**/ν esetén kapjuk. Kimutatták, hogy Re → ∞; η → 0; és Cf → 0 esetén a súrlódási együttható relatív változása olyan zavaró tényezők hatására, mint a nyomásgradiens, összenyomhatóság, nem izotermitás, porózus falon keresztül történő befecskendezés (szívás) stb. véges értéket vesz fel.
A Ψ értékének kiszámítására levezetett egyenletek egy fontos tulajdonsággal rendelkeznek, amely a Ψ-t függetleníti a turbulencia empirikus állandóitól. Az integrál “megközelítés” alapkoncepciójának megfelelően az integrál impulzusegyenletet átalakítjuk:
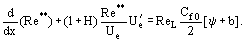
Itt,
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) a permeabilitási paraméterek arra az esetre, amikor ρw sűrűségű gáz áramlik át vw sebességgel egy átjárható falon. A Re** = Re**
függvény meghatározásához ki kell számítani az eloszlást
Ezért a zavaró tényezők szuperpozíciójának elve érvényesül
Az egyenletben. 24 minden egyes szorzó a relatív súrlódási törvényt képviseli, figyelembe véve egy-egy tényező hatását, köztük a tömöríthetőség ΨM, a hőmérsékleti (vagy entalpia) fej ΨT, a befecskendezés ΨB, a nyomásgradiens ΨP és mások.
A határréteg alapfogalmai megteremtik az olyan jelenségek magyarázatának feltételeit, mint az áramlás leválása a felületről az áramlási tehetetlenség hatására, a viszkózus áramlás lassulása a fal által és a feláramlási irányban ható kedvezőtlen nyomásgradiens = 0 vagy < 0.
Ha a nyomásgradiens kedvezőtlen az “1-4” szelvények közötti felületi helyen (lásd a 3. ábrát), a határrétegben az u = u(x,y) sebességeloszlás fokozatosan megváltozik; “kevésbé telítetté” válik, csökken a ferdeség a falhoz közelebb eső és kisebb mennyiségű mozgási energiával rendelkező folyadéksugarakban (lásd a 3. ábra sebességprofil-alakjait), amelyek messze lefelé hatolnak a megnövekedett nyomású tartományba. Egyes szakaszokon, például a “4.” szakaszon, az “a-a” áramlási vonalon (szaggatott vonal a 3. ábrán) elhelyezkedő folyadékrészecskék – miután teljesen kimerítették kinetikus energiakészletüket – lelassulnak (ua = 0).
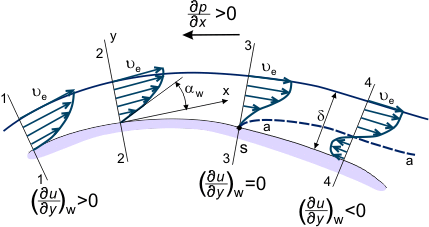
3. ábra. Határréteg fedett felület feletti áramlásban.
A statikus nyomás és a nyomásgradiens értéke nem változik a határréteg vastagságában. Ezért a falhoz az “a-a” vonalnál közelebb lévő és még kevesebb energiával rendelkező folyadékrészecskék a “4-4” szakaszon a nyomásgradiens hatására az ellenkező irányba kezdenek mozogni (lásd a 3. ábrát). Így az összefüggés:
Így a felület egyes helyein megváltozik a sebességprofil. Ezt a változást a w derivált előjelének pozitívról (2. szakasz, 3. ábra) negatívra (4. szakasz) történő megváltozása jellemzi. Természetesen az a szakasz is meghatározható, ahol w = 0 (3. szakasz, 3. ábra). Ezt nevezzük a határréteg elválasztó szakasznak (ennek megfelelően e szakasz felületén az “S” pont az elválasztási pont). Ezt egy fordított áramlási zóna kialakulása jellemzi – a test körüli áramlás már nem egyenletes, a határréteg jelentősen megvastagszik, és a külső áramlási vonalak eltérnek a körberepült test felületétől. Az elválási ponttól lefelé a statikus nyomáseloszlás a réteg vastagságán nem egyenletes, és a statikus nyomáseloszlás a felület mentén nem felel meg a külső, inviszid áramlás nyomáseloszlásának.
A leválást fordított áramlási zónák és örvények kialakulása követi, amelyekben a külső áramlásból táplált mozgási energia a súrlódási erők hatására hővé alakul át. Az áramlás szétválása, amelyet a fordított áramlású örvényzónákban történő energiaeloszlás kísér, olyan nemkívánatos hatásokat eredményez, mint a repülő járművek légellenállásának növekedése vagy a csatornák hidraulikai veszteségei.
Másrészt a szétválasztott áramlásokat különböző berendezésekben a folyadék intenzív keverésére használják (például a motorok égéstermékeiben az üzemanyag és a levegő jobb keveredésére). Ha viszkózus folyadékok változó keresztmetszetű (váltakozó nyomásgradiensű) csatornákban áramlanak, az elválasztási zóna lokális lehet, ha a diffúzorszakaszt követi a konfúzorszakasz, ahol az elválasztott áramlás ismét a felszínre tapad (lásd a 4a. ábrát). Ha az áramlás a test hátulsó élétől (például a szárny hátulsó élétől) válik el, akkor az úgynevezett örvény keletkezik “összekapcsolódó” határrétegekből (lásd 4b. ábra).
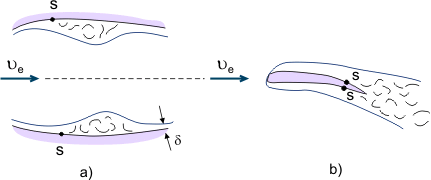
4. ábra. Határréteg leválási jelenségek.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. Kongr. – Heidelberg.
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. és Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layers, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.