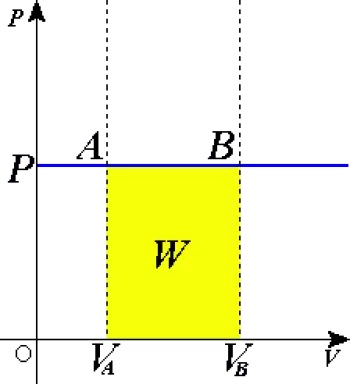
Az izobár folyamat egy bizonyos anyagmennyiség állapotában bekövetkező termodinamikai folyamatváltozás, amelyben a nyomás állandó marad. Amit megváltoztathat, az egy vagy több állapotváltozója. Ha a rendszerbe hőt adunk át, akkor munkát végzünk, és a rendszer belső energiája is megváltozik.
A nyomás-térfogat diagramon az ideális gáztörvénynek megfelelően vízszintes vonalat hajt.
Az izobár folyamatot a Charles-törvény szabályozza. Charles törvénye szerint egy állandó nyomáson lévő ideális gáz rögzített tömege esetén a térfogat egyenesen arányos a Kelvin-hőmérséklettel.
Az izobár folyamatokat a termodinamika első törvénye szabályozza. Ezekben a folyamatokban az energia növekedése egyenlő az entalpia növekedése mínusz a nyomás és a térfogat növekedésének szorzata:ΔE = ΔH – P – ΔV.
Nem tévesztendő össze az izotermikus folyamatokkal, amelyek állandó nyomáson zajlanak, vagy az adiabatikus folyamatokkal, amelyekben nincs hőcsere. Ezekben a folyamatokban nyomásváltozás következhet be. Ha a folyamat állandó térfogatban zajlik, izokorikus folyamatnak nevezzük.
Isobár folyamat példák
A termodinamikai folyamat jobb megértéséhez segít néhány példa.
-
Motor hengerének tágulási fázisa.
-
Vizet forralunk egy nyitott tartályban.
-
A földgömb felmelegedése a napsugárzás hatására.
-
A hőlégballonok izobár és izokrón folyamatot kísérelnek meg.
A léggömb levegőjének felmelegedése
A reggel kezdetén egy bizonyos nyomást, térfogatot és hőmérsékletet mutat, ahogy a benne lévő levegő felmelegszik, a nyomás megnő, de ez nem változik a térfogat növekedése miatt.
A hőmotor henger tágulási fázisa
A hőmotor hengerét a ciklus fázisától függően lehet tágítani vagy összehúzni. A levegő tágulása egy mozgó dugattyúval ellátott hengerben, amelybe hőt juttatnak, izobár folyamat révén történik. Ugyanígy a sűrítés során a térfogat izobár módon csökken.
A térfogat a hőmérsékletével arányosan nő, a nyomás pedig állandó marad. Ez összhangban van Charles törvényével.
Vízforralás nyitott edényben
Az izobár folyamat mindennapi példája a vízforralás nyitott edényben. A víznek hőenergiát adva, a víz hőmérséklete megemelkedik, és gőzzé alakul.
A kapott gőz hőmérséklete magasabb, és nagyobb térfogatot foglal el, a nyomás azonban állandó marad. Kezdettől fogva a nyomás megegyezik a légköri nyomással.
Hőlégballon fűtése
A hőlégballon az izobár folyamat példája.
A hőlégballonok azért működnek, mert a forró levegő felemelkedik. Azáltal, hogy a ballon belsejében lévő levegőt az égővel felmelegítjük, az könnyebbé válik, mint a kívül lévő hűvösebb levegő. Ennek hatására a léggömb felfelé lebeg, mintha vízben lenne.
A léggömb belsejében lévő nyomás megegyezik a légköri nyomással. Amikor a pilóta hőt fecskendez a levegőbe, a hőmérséklet emelkedik. Ezáltal csökken a levegő sűrűsége, és a levegő és a levegő sűrűsége közötti különbség miatt a léggömb felemelkedik.
Thermodinamikailag a hő egy része munkává alakul át, így a hőlégballon felemelkedik. A hő egy része a külső levegő termodinamikai érintkezése és a forró levegő tágulásakor fellépő veszteség miatt a rendszeren kívülre kerül.
W 1-2 = P ( V 2 – V 1 ) W 1-2 = n R ( T 2 – T 1 ) Q 1-2 = m c p ( T 2 – T 1 ) Q 1-2 = ( k / ( k -1)) P ( V 2 – V 1 )
Hol,
-
W 1-2 az állapotváltozással végzett munka mennyisége
-
Q 1-2 a leadott vagy elvont hőmennyiség
-
P nyomás
-
V a térfogat
-
T az abszolút hőmérséklet
-
n a por mennyisége (általában molban kifejezve)
-
m az anyag tömege
-
cp az anyag fajhője állandó nyomáson
-
k az állandó nyomáson és állandó térfogaton mért fajhő hányadosával egyenlő hányados, illetve
.
Az első egyenletből látható, hogy ha a rendszer tágul (ΔV pozitív), akkor a rendszer pozitív munkát végez. Ezzel szemben, ha a térfogatnövekedés negatív, akkor a rendszer összehúzódik, és a munka negatív.
Ideális gáz állapotegyenlete
Az ideális gáz állapotegyenlete (néha Mendelejev-Clapeyron-egyenlet vagy Clapeyron-egyenlet) egy olyan képlet, amely az ideális gáz nyomása, moláris térfogata és abszolút hőmérséklete közötti kapcsolatot határozza meg. Az egyenlet:
pV = nRT
Hol,
p – nyomás,
V- gáztérfogat,
n- a gáz mennyisége,
R – egyetemes gázállandó , R ≈ 8,314 J / (mol⋅K),
T – termodinamikai hőmérséklet, K kelvin.