Az én tippem az lenne, hogy a borkősav empirikus képletét már ismered, és a molekulatömegének segítségével kell megtalálnod a molekuláris képletét.
Tegyük fel, hogy a kiindulási pont itt a borkősav empirikus képlete így néz ki
#”C”_2 “H”_3 “O”_3 -># empirikus képlet
Most, egy vegyület empirikus képlete megmondja, hogy az alkotóelemek atomjai között milyen legkisebb egész számarányú arány van.
Ez esetben tudjuk, hogy a molekuláris képlet, amely megmondja, hogy pontosan hány atom alkotja az említett vegyület molekuláját, tartalmazni fogja
#color(black)(“2 atom C” color(red)(” for every “) {(“3 atom H”),(“3 atom O”) :}#
Lényegében az empirikus képlet többszörösét keressük.
A borkősavról azt mondjuk, hogy moláris tömege #”150 g mol”^(-1)#. A célod itt az lesz, hogy meghatározd az empirikus képletének moláris tömegét, majd ezt az értéket használd a vegyület molekuláris képletének meghatározásához.
Ez esetben
#2 xx “12.011 g mol”^(-1) “”color(blue)(+)#
#3 xx “1.00794 g mol”^(-1)#
#3 xx “15.9994 g mol”^(-1)#
#color(white)(aaaaaaaaaaaaaaaaaaaaaaaa)/color(white)(aaaaaaaaaaaaaaaaaaaaaaaaaa)#
#”75.044 g mol”^(-1) -> #az empirikus képlet moláris tömege
Ha tehát az empirikus képlet moláris tömege #”75.044 g mol”^(-1)#, és a borkősav moláris tömege #”150 g mol”^(-1)#, akkor ebből az következik, hogy az empirikus képletet meg kell szoroznunk
#(150 color(red)(cancel(color(black)(“g mol”^(-1)))))/(75.044color(red)(cancel(color(black)(“g mol”^(-1))))) = 1.999 ~~ color(red)(2)#
a molekuláris képlethez. Ez azt jelenti, hogy a borkősav molekuláris képlete
#(“C”_2 “H”_3 “O”_3)_color(red)(2) lesz, ami azt feltételezi, hogy color(green)(|bar(ul(color(white)(a/a) “C”_4 “H”_6 “O”_6color(white)(a/a)|)))#
Íme, így néz ki egy borkősav molekula
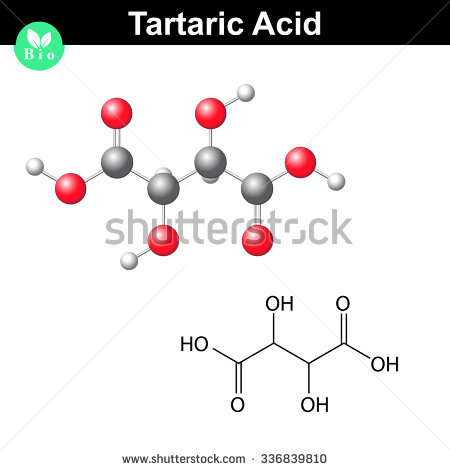
.