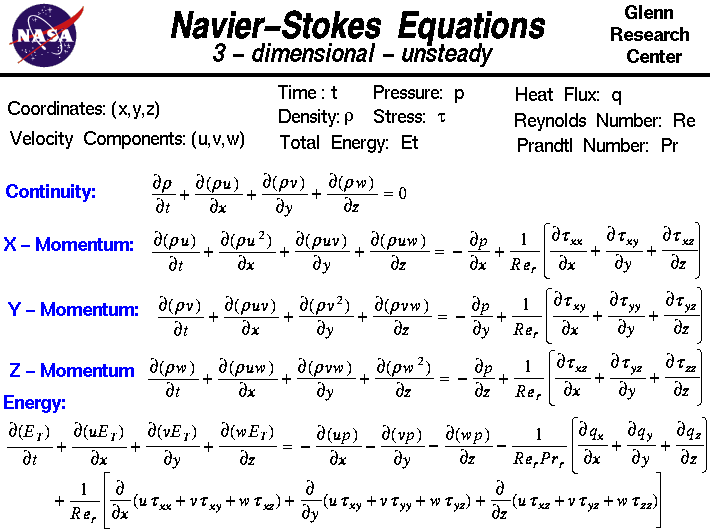
Ez a dia a Navier-Stokes-egyenletek háromdimenziós instacionárius formáját mutatja.Ezek az egyenletek leírják, hogy egy mozgó folyadék sebessége, nyomása, hőmérséklete és sűrűsége hogyan függ össze.Az egyenleteket G.G. Stokes Angliában, és M. Stokes Angliában egymástól függetlenül vezette le. Az egyenletek azEuler-egyenletek kiterjesztései, és tartalmazzák a viszkozitás áramlásra gyakorolt hatását.Ezek az egyenletek nagyon összetettek, mégis az egyetemi mérnökhallgatóknak megtanítják, hogyan kell levezetni őket egy olyan folyamat során, amely nagyon hasonló ahhoz a levezetéshez, amelyet az impulzusmegőrzés weblapon mutatunk be.
Az egyenletek kapcsolt differenciálegyenletekből állnak, és elméletileg megoldhatók egy adott áramlási problémára a számtan módszereivel.A gyakorlatban azonban ezeket az egyenleteket túl nehéz analitikusan megoldani.A múltban a mérnökök további közelítéseket és egyszerűsítéseket végeztek az egyenletkészlethez, amíg nem kaptak egy olyan egyenletcsoportot, amelyet meg tudtak oldani.A közelmúltban nagy sebességű számítógépeket használtak az egyenletek közelítésének megoldására különböző technikákkal, mint például véges differencia, véges térfogat, véges elem és spektrális módszerek.Ezt a területet nevezik számításos áramlástannak vagy CFD-nek.
A Navier-Stokes-egyenletek egy időfüggő folytonossági egyenletből állnak a tömeg megőrzésére, három időfüggő momentummegőrzési egyenletből és egy időfüggő energiamegőrzési egyenletből.A problémának négy független változója van, azx, y és z térbeli koordináták valamilyen tartományban, és a t idő. Hat függő változó van; a p nyomás, az r sűrűség és a T hőmérséklet (amely az Et összenergia révén szerepel az energiaegyenletben), valamint a sebességvektor három komponense; az u komponens az x irányban, a v komponens az y irányban, a w komponens pedig a z irányban van.A függő változók mindegyike mind a négy független változó függvénye.A differenciálegyenletek tehát parciális differenciálegyenletekés nem a közönséges differenciálegyenletek, amelyeket a kezdő számtanórán tanul.
Észreveheti, hogy a differenciálegyenlet szimbóluma eltér a szokásos “d /dt” vagy “d /dx” szimbólumtól, amelyet a közönséges differenciálegyenleteknél lát. A “
” szimbólumot a parciális deriváltak jelölésére használják.A szimbólum azt jelzi, hogy a derivált kiszámításakor az összes független változót rögzítettnek kell tartanunk, kivéve a szimbólum melletti változót. Az egyenletek halmaza:
folytonosság: r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – Momentum: (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = – p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – lendület: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = – p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – Momentum: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = – p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
Energia: Et/t + (u* Et)/x + (v * Et)/y + (w * Et)/z = – (r * u)/x – (r * v)/y – (r * w)/z
– 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {(u * tauxx + v * tauxy + w * tauxz)/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxy + v * tauyy + w * tauyz)/y + (u * tauxz + v * tauyz + w * tauzz)/z}
ahol Re aReynolds szám, amely egy hasonlósági paraméter, amely az áramlás inerciájának és az áramlásban lévő viszkózus erőknek a méretaránya. A qváltozók a hőáram komponensei és Pr a Prandtl-szám,amely egy hasonlósági paraméter, amely a viszkózus feszültségek és a hőfeszültségek aránya.A tau változók a feszültségtenzor komponensei.Egy tenzor akkor keletkezik, ha két vektort bizonyos módon megszorozunk. A sebességvektorunknak három komponense van; a feszültségtenzornak kilenc komponense van. A feszültségtenzor minden egyes komponense maga a sebességkomponensek második deriváltja.
A lendületegyenletek bal oldalán lévő kifejezéseket az egyenletek konvekciós feltételeinek nevezzük.A konvekció olyan fizikai folyamat,amely gázáramlásban játszódik le, amelyben valamilyen tulajdonságot az áramlás rendezett mozgása szállít.Az impulzusegyenletek jobb oldalán lévő, a fordított Reynolds-számmal megszorzott tagokat diffúziós tagoknak nevezzük.A diffúzió olyan fizikai folyamat, amely egy gázáramlásban játszódik le, amelyben valamilyen tulajdonságot a gázmolekulák véletlenszerű mozgása szállít.A diffúzió a feszültségtenzorral és a gáz viszkozitásával függ össze. A turbulencia és a határrétegek kialakulása a diffúzió eredménye az áramlásban.Az Euler-egyenletek csak a Navier-Stokes-egyenletek konvekciós kifejezéseit tartalmazzák, és ezért nem tudják modellezni a határrétegeket. A Navier-Stokes-egyenleteknek van egy speciális egyszerűsítése, amely a határrétegek áramlását írja le.
Megjegyezzük, hogy az összes függő változó megjelenik minden egyenletben.Az áramlási probléma megoldásához mind az öt egyenletet egyszerre kell megoldani; ezért nevezzük ezt kapcsolt egyenletrendszernek.Valójában van néhány más egyenlet is, amelyek szükségesek a rendszer megoldásához. Csak öt egyenletet mutatunk be hat ismeretlenre. Az állapotegyenlet a gáz nyomását, hőmérsékletét és sűrűségét adja meg.És meg kell adnunk a feszültségtenzor összes tagját.A CFD-ben a feszültségtenzor tagjait gyakran turbulenciamodellel közelítik.
Tevékenységek:
Tárlatvezetés
Navigáció ..
A kezdők útmutatója Kezdőoldal