By Leave a Comment on Szabadművészeti matematika

Hálók

A szilárd testek ábrázolásának egyik utolsó módja a háló használata. Ha kivágunk egy hálót, akkor azt egy alakzat modelljévé hajtogathatjuk. A hálók egyetlen szilárd test elemzésére is használhatók. Íme egy példa egy kocka hálójára.

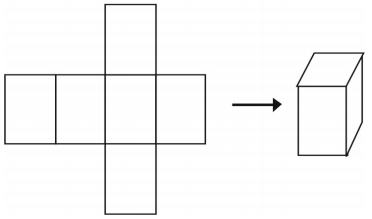
Egyetlen alakzathoz többféleképpen is készíthetünk hálót.

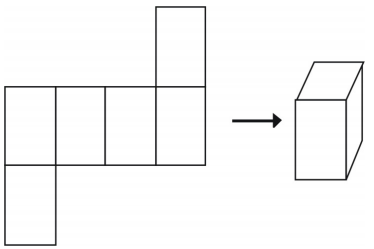
Mégis nem minden elrendezés hoz létre kockát.

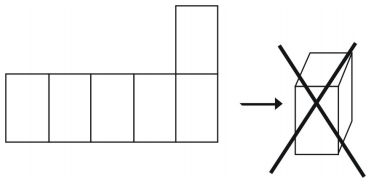
Példa 1

Milyen alakzatot hoz létre a háló? Rajzolja le az ábrát.

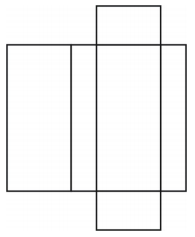
A háló egy doboz alakú négyszögletes prizmát hoz létre az alábbi ábrán látható módon.

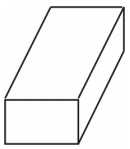
Példa 2

Milyen hálót tud rajzolni az ábrázolt alakzat ábrázolására? Rajzolja le a hálót.

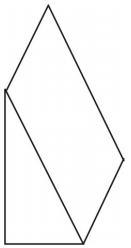
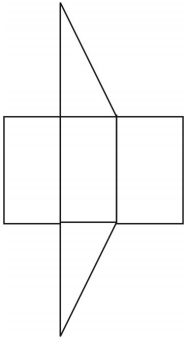
Az ábrán a prizma hálója látható. Más hálók is lehetségesek.

Áttekintő gyakorlatok

Rajzolj egy-egy hálót a következőkhöz:

Válaszok

Prizmák

A prizma olyan háromdimenziós alakzat, amelynek párhuzamos és egybeeső végei, vagyis alapjai vannak. A prizma oldalai párhuzamosak. A prizmákat az alapjaik alapján azonosítjuk.

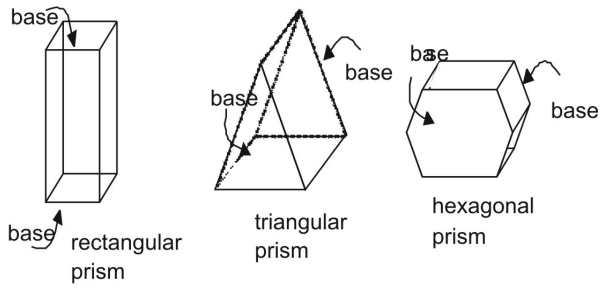
A prizma felülete hálók segítségével

A fenti prizmák derékszögű prizmák. Egy derékszögű prizmában az oldalsó oldalak merőlegesek a prizma alapjaira. Hasonlítsuk össze a derékszögű prizmát a ferde prizmával, amelyben az oldalak és az alapok nem merőlegesek egymásra.

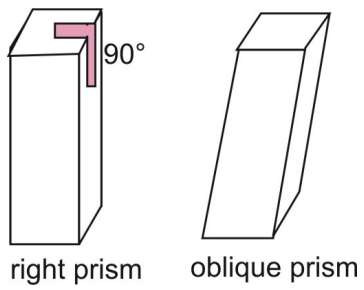
A területre vonatkozó két posztulátum a területkongruencia posztulátum és a területaddíció posztulátum.

Területkongruencia posztulátum: Ha két sokszög (vagy síkbeli alakzat) kongruens, akkor területük is kongruens.
Területi összeadás posztulátum:

Hálót és a területaddíciós posztulátumot használhatod egy derékszögű prizma felületének kiszámításához.

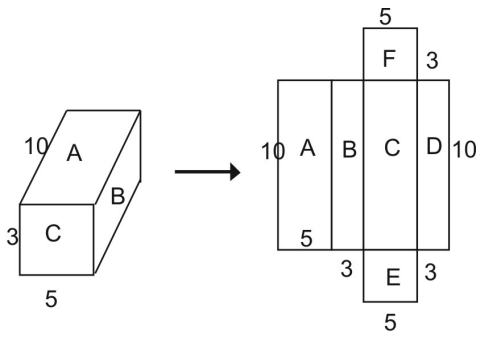
A hálóból láthatod, hogy a teljes prizma felülete egyenlő a hálót alkotó alakzatok összegével:

A teljes felület = A terület + B terület + C terület + D terület + E terület + F terület

A téglalap területének képletét felhasználva láthatod, hogy az A téglalap területe:

A = l – w
A = 10 – 5 = 50 négyzetméter

Hasonlóan a többi téglalap területét is visszahelyezzük a fenti egyenletbe.

Teljes felület = A terület + B terület + C terület + D terület + E terület + F terület
Teljes felület = (10 – 5) + (10 – 3) + (10 – 5) + (10 – 3) + (5 – 3) + (5 – 3) + (5 – 3) + (5 – 5). 3)
Teljes felület = 50 + 30 + 50 + 30 + 30 + 15 + 15
Teljes felület = 190 négyzetegység

3. példa

A prizma felületének kiszámításához használj hálót!

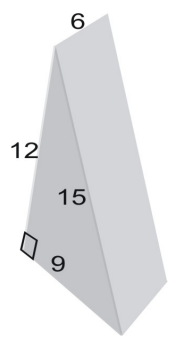
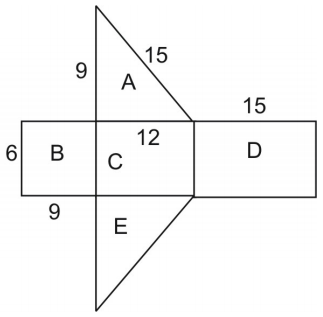
A háló területe megegyezik az ábra felületével. A háromszög területének kiszámításához a következő képletet használjuk:

\displaystyle{A}=\frac{1}{2}hb\\\ ahol h a háromszög magassága és b az alapja.

Megjegyezzük, hogy az A és E háromszögek kongruensek, így az A háromszög területét megszorozhatjuk 2-vel.

\displaystyle\text{area}=\text{area }A+\text{area }B+\text{area }C+\text{area }D+\text{area }E\\\
\displaystyle\text{ }=2(\text{area }A)+\text{area }B+\text{area }C+\text{area }D\\
\displaystyle\text{ }=2+(6\cdot9)+(6\cdot12)+(6\cdot12)\\
\displaystyle\text{ }=108+54+72+90=324\\

Thus, a felület 324 négyzetegység.

Áttekintő feladatok

Az alábbiak mindegyikére találjuk meg a felületet a hálók módszerével és a kerületet

  3. A prizma alapja egy derékszögű háromszög, amelynek lábai 3 és 4, magassága pedig 20-as. Mekkora a prizma teljes területe?
  4. Egy derékszögű hatszögű prizma 24 hüvelyk magas, és az alapjai szabályos hatszögek, amelyek oldalanként 8 hüvelyk hosszúak. Mekkora a teljes felülete?
  5. Mekkora a 4. feladatban szereplő prizma térfogata?

A következő kérdésekben egy pajta ötszögű prizma alakú, amelynek méretei lábakban vannak megadva:

  1. Hány négyzetláb (a tető nélkül) van a festendő pajta felületén?
  2. Ha egy gallon festék 250 négyzetlábat fed le, hány gallon festékre van szükség a pajta festéséhez?
  3. A kartondoboz egy tökéletes kocka, amelynek az éle 17 hüvelyk. Hány köbmétert tud befogadni?
  4. A medence 16 láb széles, 32 láb hosszú és egyenletesen 4 láb mély. Hány köbláb víz fér el benne?
  5. Egy gabonapelyhes doboz hossza 25 cm, szélessége 9 cm, magassága 30 cm. Mennyi gabonapehely fér bele?

Válaszok

Háló és kerület:

  1. 40,5 in2
  2. 838 cm2
  3. 252 négyzetegység
  4. 1484.6 négyzetegység
  5. 3990,7 köbcenti

A pajta:

  1. 2450 négyzetláb
  2. 10 gallon festék
  3. 2,85 köbcenti (itt óvatosan. A feladatban az egységek hüvelykben vannak megadva, de a kérdés lábakat kérdez.)
  4. 2048 köbláb
  5. 6750 cm3

Henger

A henger olyan háromdimenziós alakzat, amelynek párhuzamos és egybeeső kör alakú végei, vagy alapjai vannak. A henger egyetlen ívelt oldala van, amely síkba fektetve téglalapot alkot.

A prizmákhoz hasonlóan a hengerek is lehetnek derékszögűek vagy ferdék. A derékszögű henger oldala merőleges a kör alakú alapokra. Egy ferde henger oldala nem merőleges az alapjaira.

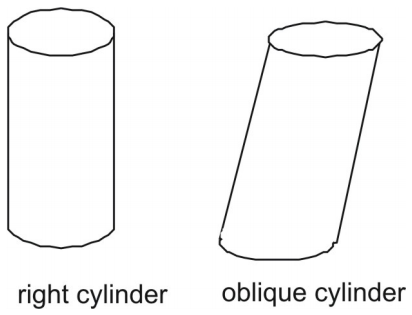
A henger felülete hálók segítségével

Egy hengert hálóra bonthatunk.

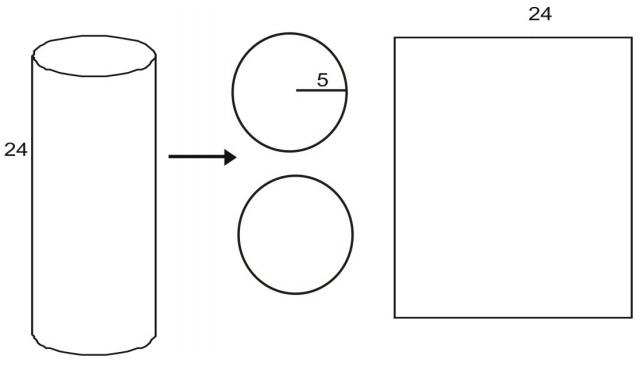
Az egyes alapok területét a kör területe adja:

A=\pi{r}^2\\\
A=\pi(5)^2\\\
A=25\pi\\
A\approx(25)(3.14)=78.5\\\

A négyszögletes oldalfelület L területét a szélesség és magasság szorzata adja. A magasságot 24-nek adjuk meg. Láthatjuk, hogy a terület szélessége megegyezik a kör alakú alap kerületével.

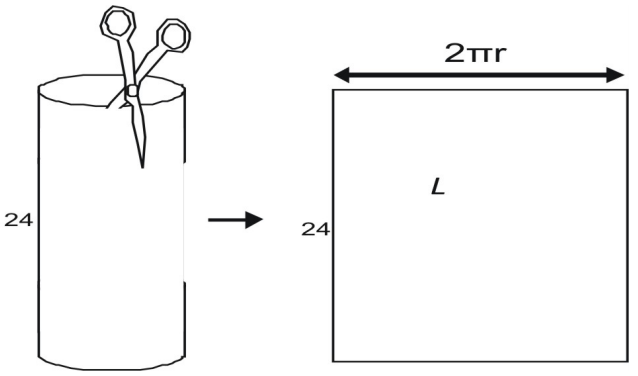
A szélesség megtalálásához képzeljük el, hogy egy konzervdobozszerű hengert egy ollóval szétszedünk. Ha levágod az oldalsó területet, látod, hogy az megegyezik a konzervdoboz tetejének kerületével. A kör kerülete C = 2πr, az oldalsó terület, L,

L=2{\pi}rh\\\
L=2{\pi}(5)(24)\\\
L=240\pi\\\
L\approx(240)(3.14)=753.6\\\

Most az A = (a két alap területe) + (az oldalsó oldal területe) segítségével meg tudjuk találni a teljes henger területét.

A=2(75.36)+753.6\\\
A=904.32\\\

Láthatjuk, hogy a teljes felület meghatározására használt képlet bármelyik derékszögű hengerre alkalmazható.

Egy derékszögű henger területe: Egy sugárral és h magassággal rendelkező derékszögű henger felületét A = 2B + L adja meg, ahol B a henger minden egyes alapjának területe, L pedig a henger oldalfelülete.

4. példa

Hálót használj a henger felületének meghatározásához.

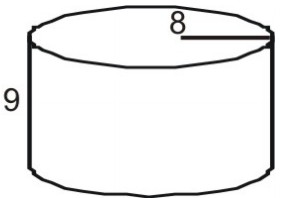
Először rajzoljuk meg és címkézzük fel az ábra hálóját.

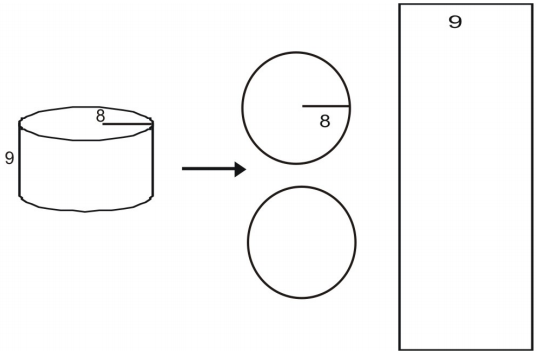
Kalkuláljuk ki az egyes alapok területét.

A=\pi{r}^2\\\
A=\pi(8)^2\\\
A=64\pi\\
A\approx(64)(3.14)=200.96\\

Calculate L.

L=2{\pi}rh\\
L=2{\pi}(8)(9)\\
L=144\pi\\
L\approx(144)(3.14)=452.16\\

Következtessük a teljes henger területét.

A=2(200.96)+452.16\
A=854.08\\\

Így a teljes felület megközelítőleg 854,08 négyzetegység

A henger felülete képlet segítségével

Láttad, hogyan használhatod a hálókat egy henger teljes felületének kiszámításához. A posztulátumot fel lehet bontani, hogy egy általános képletet alkossunk minden derékszögű hengerre.

A = 2B + L

Megjegyezzük, hogy bármely henger alapterülete, B, a következő: B = πr2

Minden henger oldalfelülete, L, a következő:

L=\text{az oldalfelület szélessége}\cdot\text{a henger magassága}\\
L=\text{az alap kerülete}\cdot\text{a henger magassága}\\
L=2\pi{r}\cdot{h}\\\\

A két egyenletet összeadva megkapjuk:

Az egyenletből a-t kiszámítva megkapjuk:

A derékszögű henger felülete: Egy r sugarú és h magasságú derékszögű henger a következőképpen fejezhető ki:

A = 2πr2 + 2πrh

vagy:

A = 2πr(r + h)

A képleteket bármely derékszögű henger területének kiszámítására használhatjuk.

5. példa

A képlet segítségével megkeresheted a henger felületét.

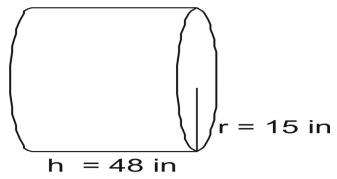
Írd fel a képletet, helyettesítsd be az értékeket és oldd meg.

A=2(\pi{r}^2)+2\pi{rh}\\
A=2(3.14)(15)(15)+2(3.14)(15)(48)\\
A=1413+4521.6\\
A=5934.6\text{ négyzet hüvelyk}\\\

Példa 6

Meghatározzuk a henger felületét.

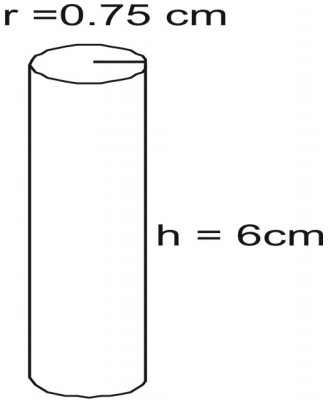
Írd fel a képletet, helyettesítsd be az értékeket és oldd meg.

A=2\pi{r}(r+h)\\\
A=2(3,14)(0,75)\\\
A=31.7925\text{ négyzetcentiméter}\\\

7. példa

Következtessük egy 4 cm sugarú és 226,08 négyzetcentiméter felületű henger magasságát.

A megadott adatokkal írjuk fel a képletet és oldjuk meg h-ra.

A=2\pi{r}(r+h)\\
226,08=2(3,14)(4)\\
226,08=25,12\\
226,08=100,48+25,12h\\\
5=h\\

Gömbök

A gömb olyan háromdimenziós alakzat, amely gömb alakú.

A gömböket háromféleképpen jellemezhetjük.

  • A gömb azoknak a pontoknak a halmaza, amelyek egyetlen O középponttól r rögzített távolságra vannak.
  • A gömb az a felület, amely akkor keletkezik, ha egy kört bármelyik átmérője körül elforgatunk.

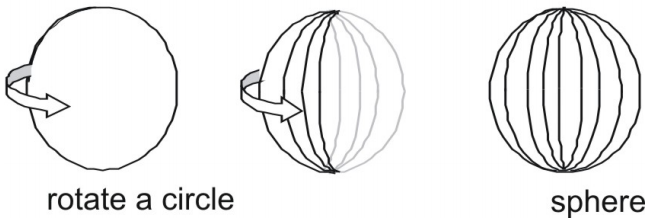
A gömb felülete

Gömbök és hengerek méréseiből következtethetünk a gömb felületének képletére. Itt egy 3 sugarú gömböt és egy 3 sugarú és 3 magasságú derékszögű hengert mutatunk, és a területet π-ben fejezzük ki.

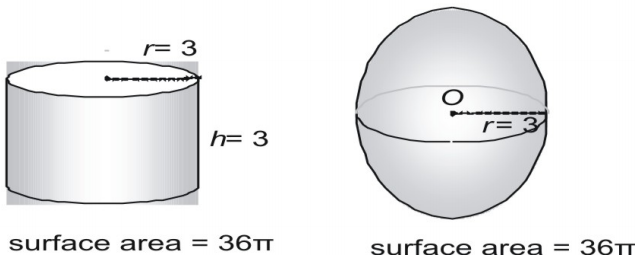
Most próbáljuk ki egy nagyobb párral, a felületet tizedes formában kifejezve.

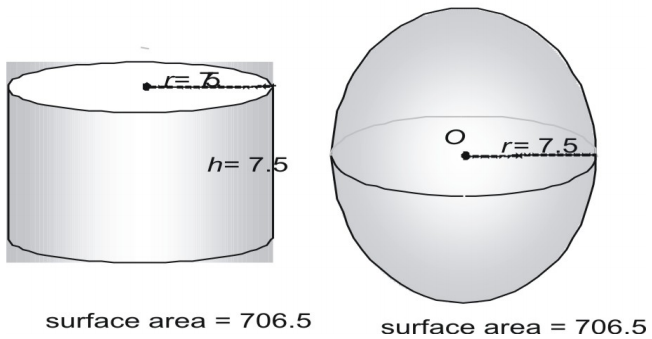
Nézzünk meg egy harmadik párt.

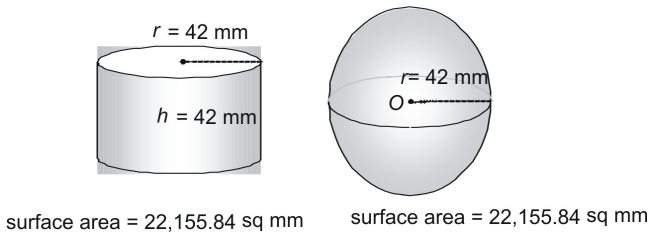
Véletlen, hogy egy gömb és egy henger, amelynek sugara és magassága megegyezik a gömb sugarával, pontosan ugyanolyan felületű? Egyáltalán nem! Valójában az ókori görögök használtak egy módszert, amely megmutatta, hogy a következő képlet segítségével bármely gömb (vagy bármely henger, amelyben ) felületét meg lehet találni.

A gömb felületét a következő adja meg: A = 4πr2

8. példa

Következtessük egy 14 láb sugarú gömb felületét.

A képletet használjuk.

A=4\pi{r}^2\\\
A=4\pi(14)^2\\\
A=4\pi(196)\\\
A=784\pi\\
2461.76\text{ négyzetláb a }3.14\text{ segítségével \pi\\

Példa 9

Meghatározzuk az alábbi ábra felületét π-vel kifejezve.

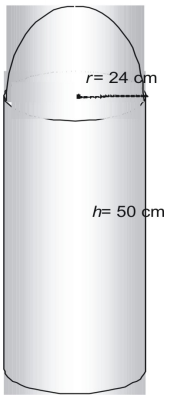
Az ábra egy félgömbből vagy félgömbből és egy hengerből áll a teteje nélkül.

A(\text{half sphere})=\frac{1}{2}A(\text{sphere})\\
A(\text{half sphere})=\frac{1}{2}\cdot4\pi{r}^2\\
A(\text{half gömb})=2\pi(576)\\\
A(\text{félgömb})=1152\pi\text{ négyzet cm}\\

Most találjuk meg a henger területét a teteje nélkül.

A(\text{topless cylinder})=A(\text{cylinder})-A(\text{top})\\
A(\text{topless cylinder})=2(\pi{r}^2)+2\pi{rh}-\pi{r}^2\\
A(\text{topless cylinder})=\pi{r}^2+2\pi{rh}\\
A(\text{topless cylinder})=\pi(576)+2\pi(24)(50)\\
A(\text{topless cylinder})=2976\pi\text{ square cm}\\

Thus, a teljes felület 1152\pi+2976\pi=4128\pi\\\

Értekező feladatok

  1. Keresd meg annak a gömbnek a sugarát, amelynek a térfogata 335 cm3.
  2. Meghatározzuk ennek az alakzatnak a felületét és térfogatát:
  3. A gömb sugara 4. Határozzuk meg a térfogatát és a teljes felületét.
  4. A gömb sugara 5 cm3. Egy derékszögű henger, amelynek azonos sugara van, ugyanolyan térfogattal rendelkezik. Határozzuk meg a henger magasságát és teljes felületét.
  5. Gömb: térfogata = 296 cm3. Keressük meg az átmérőt.
  6. Gömb: felülete 179 in2 . Határozzuk meg a sugarat.
  7. A 3,5 hüvelyk átmérőjű teniszlabdákat háromdobozos dobozokban árulják. A konzervdoboz egy henger. Tegyük fel, hogy a labdák a konzervdoboz oldalain, tetején és alján érintkeznek. Mekkora a teniszlabdák által nem elfoglalt térfogat?
  8. A gömb felülete 36π in2 . Határozzuk meg a térfogatát.
  9. Egy daru által működtetett óriáskanna félgömb alakú, sugara = 21 hüvelyk. A kanál tele van olvasztott forró acéllal. Amikor az acélt egy hengeres tárolótartályba öntjük, amelynek sugara 28 hüvelyk, az olvadt acél hány hüvelyk magasra emelkedik?

Válaszok

Megjegyezzük, hogy ezekben a feladatokban π-t használunk, nem pedig 3,14-et.

  1. 1. Sugár = 4,31 cm
  2. felület = 706,86 cm2
    térfogat = 1767,15 cm3
  3. térfogat = 268,08 egység3
    felület = 201,06 egység2
  4. magasság = 20/3 egység teljes felület = 366,52 egység2
  5. átmérő = 8,27cm
  6. sugár = 3.77 hüvelyk
  7. A henger térfogata = 32.16π in3 a teniszlabdák térfogata = 21.44π in3
    A teniszlabdák által nem elfoglalt térfogat = 33.68 in3
  8. Térfogat = 113.10 in3
  9. A hengerben lévő olvadt acél magassága 7.88 inch

lesz.

Vélemény, hozzászólás?

Az e-mail-címet nem tesszük közzé.