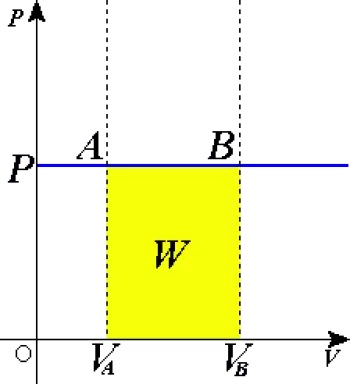
等圧過程とは、圧力が一定で、ある量の物質の状態が変化する熱力学的過程のことである。 変化させるものは、その状態変数の1つ以上である。 熱が伝われば仕事が行われ、系の内部エネルギーも変化する。
圧力-体積図では理想気体の法則に従って水平線を駆動する。
等圧過程はシャルルの法則によって支配されている。 シャルルの法則によると、一定の圧力で一定の質量の理想気体の場合、体積はケルビン温度に正比例する。
等圧過程は熱力学の第一法則に支配されている。 これらの過程では、エネルギーの増加はエンタルピーの増加から圧力を引いたものに体積の増加をかけたものに等しい：ΔE = ΔH – P – ΔV.
一定の圧力で行われる等温過程や熱交換しない断熱過程と混乱しないようにしなければならない。 これらのプロセスでは、圧力変化が起こりうる。 一定の体積で行われる場合は等温過程と呼ばれる。
等温過程の例
この熱力学的過程をよりよく理解するためには、いくつかの例を見てみるとよい。
-
エンジンのシリンダーの膨張相
-
開放容器で水を沸騰させる。
-
太陽放射の影響による地球の加熱
-
熱気球による等圧過程と等温過程の実験
風船の空気加熱
朝の始まりには一定の圧力、体積、温度を示し、内部の空気が加熱されると圧力が上昇するが、これは体積の増加によって変化しない。
熱機関のシリンダー膨張段階
熱機関のシリンダーはサイクルの段階によって拡張または収縮することが可能である。 熱の供給される可動ピストンを持つシリンダー内の空気の膨張は、等圧過程によって行われる。 同様に圧縮時には、体積は等圧的に減少する。
体積はその温度に比例して増加し、圧力は一定に保たれる。
開放容器で水を沸かす
等圧過程の日常的な例として、開放容器で水を沸騰させることが挙げられる。
得られた蒸気は温度が高く、体積が大きくなるが、圧力は一定である。
熱気球の加熱
熱気球は等圧過程の一例である。
熱気球が機能するのは、熱い空気が上昇するためです。 バーナーで風船内の空気を加熱することで、外側の冷たい空気より軽くなります。
気球の中の圧力は、大気圧と同じです。 パイロットが空気に熱を加えると、温度が上昇します。
熱力学的には、熱の一部が仕事に変換され、熱気球が上昇する。
W 1-2 = P ( V 2 – V 1 ) W 1-2 = n R ( T 2 – T 1 ) Q 1-2 = m c p ( T 2 – T 1 ) Q 1-2 = ( k / ( k -1) ) 熱風が上昇するとき、熱力学的に熱の一部は仕事に変換され、系外に放出される。 P ( V 2 – V 1 )
Where,
-
W 1-2状態変化により行われる仕事量
-
Q 1-2 供給または除去された熱量
-
P 圧力
-
V 体積
-
T 絶対温度
-
n 塵量（通常モルで表されます）
-
mは物質の質量
-
cpは定圧での物質の比熱
-
kは定圧と定容での比熱の商に相当する比である。 それぞれ
最初の式から、系が膨張すれば（ΔVが正）、系は正の仕事をすることがわかる。 逆に、体積の増加が負であれば、系は収縮し、仕事は負になる。
理想気体の状態方程式
理想気体の状態方程式（Mendeleev – Clapeyron equationまたはClapeyron equationということもある）は、理想気体の圧力、モル体積、絶対温度の関係を定める式である。
pV = nRT
ここで、
p – 圧力、
V – 気体量、
n – 気体の量、
R – 普遍気体定数 , R ≈ 8.314 J / (mol⋅K),
T – 熱力学的温度、Kケルビン
…です。