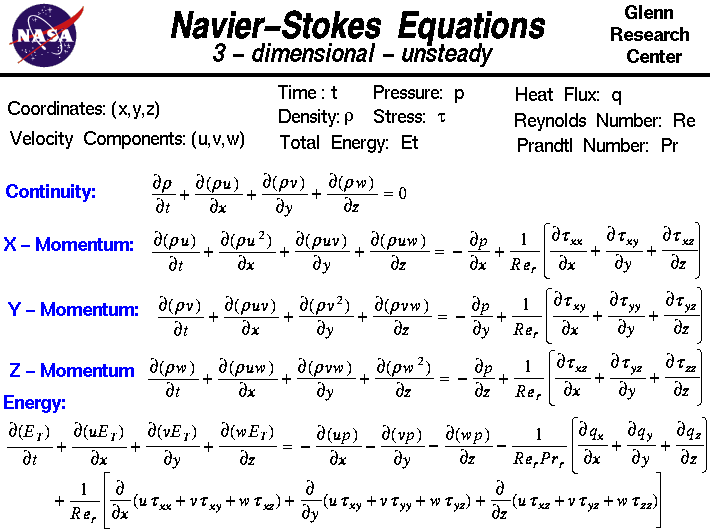
このスライドでは、ナビエ・ストークス方程式の3次元非定常形状を示します。この方程式は、移動する流体の速度、圧力、温度、密度がどのように関連するかを記述しています。 これらの方程式は非常に複雑ですが、工学部の学部生は、運動量の保存のWebページで紹介している導出と非常によく似たプロセスで導出する方法を教わります。
方程式は連立微分方程式の集合であり、理論的には微積分の方法を用いて与えられた流れの問題を解くことができます。この研究分野は計算流体力学またはCFDと呼ばれている。
ナビエ・ストークス方程式は、質量保存のための時間依存連続性方程式、3つの時間依存モーメント保存方程式、時間依存エネルギー保存方程式から構成されている。 従属変数は6つあり, 圧力 p, 密度 r, 温度 T (これは全エネルギー Et を通してエネルギー方程式に含まれる) と速度ベクトルの3成分 (u 成分は x方向, v 成分は y方向, w 成分は z方向) である.すべての従属変数は4つの独立変数すべての関数である.独立変数と速度ベクトルの3成分とは, x方向, y方向および z方向で異なる.
この微分方程式は偏微分方程式であり、微積分の初歩で学ぶ常微分方程式ではありません。常微分方程式で見られる「d /dt」や「d /dx」とは異なる記号であることに気がつくと思います。 この記号は，微分の計算をするときに，隣の変数以外の独立変数をすべて固定することを意味しています。 4220>
連続の式がある: 
r/t + (r * u)/x + (r * v)/y + (r * w)/z = 0
X – 運動量.勾配.勾配.勾配.勾配.勾配は勾配を表す。 (r * u)/t + (r * u^2)/x + (r * u * v)/y + (r * u * w)/z = -となる。 p/x
+ 1/Re * { tauxx/x + tauxy/y + tauxz/z}
Y – モメンタム……………………………..: (r * v)/t + (r * u * v)/x + (r * v^2)/y + (r * v * w)/z = -となる。 p/y
+ 1/Re * { tauxy/x + tauyy/y + tauyz/z}
Z – モメンタム: (r * w)/t + (r * u * w)/x + (r * v * w)/y + (r * w^2)/z = -となる。 p/z
+ 1/Re * { tauxz/x + tauyz/y + tauzz/z}
エネルギーを示します。 Et/t + (u* Et)/x + (v* Et)/y + (w* Et)/z = – (r* u)/x – (r* v)/y – (r* w)/z – となる。 1/(Re*Pr) * { qx/x + qy/y + qz/z}
+ 1/Re * {（uの場合 * tauxx + v * tauxy + w * tauxz）/x + (u * tauxy + v * tauyy + w * tauyz)/y + (u *) tauxz + v * tauyz + w * tauzz)/z}
ここでReはレイノルズ数で、流れの慣性力と流れの粘性力のスケーリングの比である類似性パラメータである。 q変数は熱流束成分であり、Prはプランドル数で、粘性応力と熱応力の比である類似性パラメータである。 速度ベクトルは3成分で、応力テンソルは9成分である。 4220>
運動量方程式の左辺の項は対流項と呼ばれる。対流とは、気体の流れの中で起こる物理現象で、流れの秩序だった運動によってある性質が運ばれることである。運動量方程式の右辺の逆レイノルズ数を乗じた項を拡散項と呼ぶ。拡散は気体の流れの中で起こる物理現象で、気体の分子のランダムな運動によってある性質が輸送されるものである。 乱流や境界層の生成は、流れにおける拡散の結果である。Euler方程式はNavier-Stokes方程式の対流項のみを含んでおり、境界層をモデル化することはできない。
各式にすべての従属変数が現れることに注目してほしい。流れの問題を解くには、5つの方程式を同時に解かなければならない。 この系を解くのに必要な方程式は他にもあるのですが、ここでは6つの未知数に対する5つの方程式だけを示しています。 また、応力テンソルの項をすべて指定する必要がある。CFDでは応力テンソルの項はしばしば乱流モデルで近似される。
活動:
ガイドツアー
ナビゲーション …
ビギナーズガイド ホームページ