境界層とは、動いている流れに接する壁の固体表面に近い粘性流体の薄い層で、（その厚さδの範囲内で）流速が壁でゼロ（粘性のために流れが壁に「くっつく」）から境界でUeまで変化し、これはおよそ（1%の誤差で）自由流速と対応する（図1参照）。 厳密には、流体と固体間の分子間相互作用に依存する摩擦力は、壁からの距離に応じて減少し、無限大でゼロに等しくなるので、δの値は任意の値である。
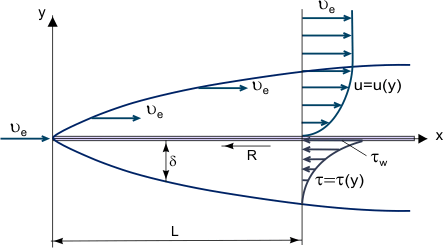
図1. 平板上の境界層の成長。
境界層の基本概念はL. Prandtl（1904）によって提案され、境界層はレイノルズ数Reが非常に大きい流れ、つまり慣性力に比べて粘性が比較的小さい流れで発生する流体層と定義された。 これは、物体が高速の気流にさらされる場合や、物体が非常に大きく、気流の速度が中程度である場合に観察される。 この場合、比較的薄い境界層では、摩擦シアストレス（粘性せん断力）：τ＝η（ここで、ηは動的粘性、u＝u（y）-境界層縦速度成分の「プロファイル」、図1参照）が非常に大きくなり、特に、u＝0、τw＝ηwの壁では粘性自体はかなり小さいかもしれないが、摩擦シアストレスが大きくなる可能性がある。
境界層外の摩擦力を無視し、Prandtlの概念に基づいて、摩擦効果の大きい境界層とほとんど非粘性流の核の2つの流れ領域を考えることができる。 境界層は非常に薄い層（δ<< L、ここでLは流れが発生する物体または流れを含む流路の特性線寸法、その厚さはReの増加とともに減少する、図1）という前提で、次の関係から境界層の厚さのオーダーを推定することができる。
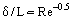
例えば、飛行機がUe=400km/hrで飛ぶとき、1mの弦（プロファイル長）の翼後縁の境界層厚は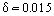
mである。 実験的に確立されたように、本体の入口部では層流境界層が発達している。 しかし、いくつかの不安定要因の影響により、境界層は徐々に不安定になり、乱流領域へ移行する。 乱流領域と層流領域の間に遷移領域が存在することは、特殊な実験研究によって確立されている。 ある場合（例えば、外部流れの乱れが大きい場合）には、流れの淀み点の直下で境界層が乱流となる。
境界層は比較的薄いにもかかわらず、流れと物体との動的な相互作用を開始するのに非常に重要である。 境界層は、飛行体の空気力学的抗力と揚力、あるいは流路における流体の流れのエネルギー損失を決定する（この場合、熱伝達の熱力学的相互作用を決定する熱境界層も存在するので、流体力学的境界層となる）。
境界層パラメータの計算は、粘性流体の運動に関するナビエ・ストークス方程式から得られる方程式の解に基づいており、まず境界層の薄さを考慮してかなり単純化される。
L・プランドルが提案した解は、本質的にはナビエ・ストークス方程式の冪級数展開の第1項で、無次元パラメータ（ΔL）の累乗について展開が行われる。 この項の小さい方のパラメータはゼロ乗であり、境界層方程式の漸近展開(大きなReでの)におけるゼロ近似となる(漸近的な解)。
ナビエ・ストークス方程式から境界層方程式への変換は、物体力のない2次元非圧縮性流れの層流境界層に対するプランドル方程式を導くことで実証できる。
この場合、ナビエ・ストークス方程式系は:
式のいくつかの項の大きさの桁を評価した後,式(1)を求めると、
> > >が得られる。 (2)のいくつかの項の大きさのオーダーを評価し、小さな項を無視すると層状境界層に対するPrandtl方程式系は次のようになる:
ここでx、yは縦、横座標（図1）、vはy軸の速度成分、pは圧力、tは時間、nは動粘性率である。
境界層は薄く、その外縁部での速度Ueは、境界層が外部の流れに及ぼす逆作用を考慮せず、第一近似まで計算した壁に沿った理想（非粘性）流体の速度として十分かつ正確に決定することが可能である。 式（3）の縦方向の圧力勾配＝（p（y）＝constのとき）は、理想流体の運動方程式であるEuler方程式から描くことができる。 以上より、有限形のPrandtl方程式は、以下のように書かれることになる。
これは初期条件と境界条件
式（4）は速度成分uとvの実際の値に対して書かれる2次の放物型非線形偏微分方程式系である。 乱流について得られた方程式を一般化するには、乱流パラメータの実測値、平均値、脈動成分間のよく知られた関係を用いる必要がある。 例えば、速度成分では、実測値u、v、平均値ū、
、脈動成分u’、v’を結ぶ関係が存在する。
いくつかの並べ替えの後、特に定常流については、系(3)から別の方程式を得ることができる：
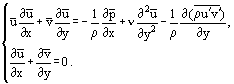
境界層における摩擦せん断応力に次の関係式を使う。
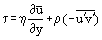
そして層流境界層ではu=u’と
を考慮すると、プランドル方程式を層流と乱流の両方に有効な形で書き直すことができる。
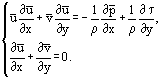
最も簡単な解は薄い平板上の層流境界層で、非圧縮性流体の2次元平行流である（図1）。 この場合、方程式の項：x〜L、y〜δ、δ〜
の大きさの順序を推定することにより、変数xとyを一つの関係
に結合し、式（8）（dp/dx=0時）を新しいパラメータxに対するuとvの依存性を決めることに還元することができる。 一方、速度成分u, vと流線関数ψ
の間のよく知られた関係を用いると、3階の普通の非線形微分方程式を一つ得ることができる。 偏微分方程式系(8)
ここで、f(ξ)はξ変数の未知関数である。 f = ƒ=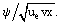
式(1)の最初の数値解は、(1)と(2)を足したものである。 (10)の最初の数値解はBlasius(1908)によってy=0の境界層の物理条件に相当する境界条件：u=0, v=0; at y→∞; u→Ue (Blasius boundary layer)で得られた。
図2はBlasius解（実線）と実験データを比較した結果である。 これらのデータを用いて、粘性境界層の厚さを評価することができる。 ξ 
2.5では、(u/Ue 0.99)となり（図2）、式（9）から、
が得られる。
壁面摩擦せん断応力におけるf(ξ)関数の2階微分の値のBlasius数値計算から、この場合の関係は、
また、L長の板（図1）の両面に働く摩擦力Rは式から決定される。 (11):
平板の摩擦係数のように:
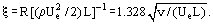
プラントール方程式はナビエ・ストークス方程式よりはるかに簡単であるにもかかわらず、その解は限られた問題しか得られていない。 多くの実用的な問題では、境界層内の速度プロファイルを求める必要はなく、厚さとシアストレスだけを求めることができる。 このような情報は積分運動量方程式
この積分関係は層流境界層でも乱流境界層でも成り立つ。
事前には知られていないが層厚δにわたる流体パラメータの分布を特徴付ける関数は式（12）の積分に含まれることになる。 そして、その積分の計算誤差は、近似的に仮定した積分関数ρu = ρu(y)の誤差よりも小さくなっている。 これらのことから、プランドル方程式を積分する厳密な方法よりも時間のかからない境界層パラメータの近似的な計算方法を開発する条件が整った。 この基本概念はT. von Karmanが最初に提案したもので、任意の層厚δ*
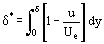
および運動量変位厚δ**
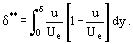
を導入すると式（1）が変形できるようになり、そのため、この式は(15)のようになる。 (
式(15)にはδ* = δ*(x), δ** = δ**(x), τw = τw(x) という三つの未知関数が含まれる. (15)のような常微分方程式を解くには、通常、境界層厚さ方向の速度分布(速度プロファイル)をいくつかの特徴的なパラメータ(フォームパラメータ)の関数として仮定(または表現)し、摩擦係数Cf = 2τw/(ρU2e) と任意の境界層厚さの関係 (摩擦法則)に関して経験則を使う必要があります。
δ*、δ**に関する数値についてはいくつかの明確な物理説明が与えられます。 式(13)の積分関数には(Ue – u)という速度減少を特徴づける項が再配列の後に含まれている。 したがって、式(14)の積分は、速度 Ue での完全な流体 の流れと比較して、境界層を越える流量の減少を示す指標と見なすことができ る。 一方、δ*の値は、摩擦力の影響による外部流線の壁面に対する法線方向（y軸方向）のずれを示す指標と考えることができる。 このように式（14）の積分構造を考察すると、δ**は摩擦の影響下での境界層での運動量減少を特徴づけるものと結論づけることができる。
以下の関係が成り立つ：
ここでHは境界層速度プロファイルの形状パラメータである。 例えば、線形分布u=kyの場合、
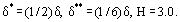
現在、乱流境界層パラメータの予測には、いわゆる半経験的理論が広く用いられている。 この場合、乱流境界層における全摩擦応力τは和
ここで、τTは追加（乱流またはレイノルズ）摩擦応力で、特に非圧縮性流れでは
式（1）を参照する。 (7)を参照。
この表現は境界層での運動方程式系(6)と直接的に関連している。 圧縮性境界層では密度脈動は温度脈動
ここでβ=(1/T)は体積膨張係数
またτTを求めるには乱流運動量伝達に関する半経験則が使用されている。 例えば、
ここでηTは1877年にJ.Boussinesqが導入した乱流粘性の動的係数である。
Prandtlは分子と乱流交換の類似性の概念（類似性理論）に基づいて混合長（die Mischungsweg）仮説を発表した。 混合長1とは、有限の流体体積（「モル」）が運動量を変えずに平均運動のある層から別の層へ通過する道筋のことである。 この条件に従って、彼は境界層理論の基礎となる方程式を導いた：
壁際流境界層の乱流領域に対して、L.M.M.S.A.を導入した。 Prandtlはy
ここでκは経験定数。
壁に近いところではηT << ηで、粘性分子摩擦が決定要因である。 この部分の境界層δ1(層流層または粘性副層と呼ばれる)の厚さは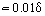
である。 副層の外側ではηTの値が大きくなり、ηよりも数桁大きくなる。 これに対応して、この乱流コアと呼ばれる境界層の領域では、τT > 0 = ηとなる。 乱流コアは、層流摩擦と乱流摩擦が同程度のバッファゾーンと、τT > > τ0となる発達ゾーンに細分化されることもある。 この領域では、式(18)を積分し、式(19)を考慮すると、対数速度分布の式が導かれる。
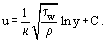
無次元（または普遍）座標が用いられる場合
ここで
はいわゆる動的速度（または摩擦速度）、式.は(19)式(20)の対数速度分布の式である。 (20)は次のように書き換えられる。
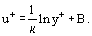
ユニバーサル座標での速度分布表現と乱流粘性係数の数学モデルについては乱流の項で詳しく説明する。 S. KutateladzeとA. I. Leontievによって開発された半経験的乱流境界層理論では、Re → ∞において層流（粘性）下層の厚さδ1がδより高い割合で減少し、その結果（δ1/δ）→0といういわゆる漸近理論に基づいており、この条件では「消失粘性」の乱流境界層が発達していると言える。 この層では、η → 0 だがゼロにはならず、この点で完全流体流れとは異なる。 S. S. Kutateladze と A. I. Leontiev (1990)によって導入された相対摩擦法則の概念は
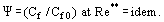
非圧縮性、等温流で飛び回る平らな不透水性プレート上の「標準」条件のCf0に対する検討条件の摩擦係数Cfの比として定義し、両係数は Re** = Ueδ**/ν に対して得られる。 Re →∞η →0; Cf →0において、圧力勾配、圧縮性、非等温性、多孔質壁からの注入（吸引）などの擾乱因子の影響下での摩擦係数の相対変化は有限の値を持つことが示された。 積分「アプローチ」の基本概念に従って、積分運動方程式は次のように変形される：
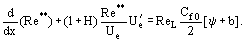
ここで、
ReL = UeL/ν, b = (2/Cf0)(ρwUw)/(ρeUe) は速度vwで透水壁を通して密度ρwのガスを注入する場合の透水係数である。 関数Re**＝Re**
を求めるためには、分布
を計算する必要がある。このためには、妨害因子の重ね合わせの原理
式中、(24)は、(1)と(2)を足したものである。 24において、各乗数は、圧縮率ΨM、温度（またはエンタルピー）ヘッドΨT、注入ΨB、圧力勾配ΨP等のうち、一つの要因の影響を考慮した相対摩擦法則を表している。
境界層の基本概念は、流れの慣性の影響による表面からの流れの剥離、壁による粘性流の減速、上流方向に働く逆圧力勾配＝0または<0などの現象を説明するための条件を作り出すものである。
セクション1-4間の表面位置で圧力勾配が逆である場合（図3参照）、境界層内の速度分布u=u(x,y)は徐々に変化し、壁に近く、運動エネルギー量が少ない流体ジェット（図3の速度プロファイル形状参照）は、圧力上昇領域の下流まで入り込んで「充実しなく」なり傾斜が小さくなっている。 いくつかのセクション、たとえばセクション4では、「a-a」流線（図3の点線）上にある流体粒子は、運動エネルギーの供給を完全に使い果たして、減速する（ua = 0）。
静圧と圧力勾配の値は境界層の厚さによって変わることはない。 したがって、線a-aよりも壁に近く、より少ないエネルギーしか持たない流体粒子は、4-4’セクションで圧力勾配の影響を受けて反対方向に移動し始める(図3参照)。 したがって、
このように、表面のある位置で、速度プロファイルが変化する。 この変化は、微分値wの符号が正（2項、図3）から負（4項）に変化することで特徴付けられる。 もちろん、w = 0となる区間を定義することも可能である（図3の3区間）。 これを境界層分離区間と呼ぶ(この区間の表面上の点Sが分離点となる)。 この区間は逆流域が発生することが特徴で、本体周囲の流れは滑らかでなくなり、境界層はかなり厚くなり、外部の流線は本体表面から逸脱している。
分離の後、逆流域や渦が発生し、外部の流れから供給された運動エネルギーが摩擦力の影響を受けて熱に変わる。
一方、分離した流れは、流体の集中的な混合（例えば、エンジンの燃焼室における燃料と空気の混合を改善するため）のためのさまざまな装置で使用されている。 粘性流体が可変断面（交互圧力勾配）を有するチャネル内を流れる場合、ディフューザセクションの後にコンフューザセクションが続くと、分離した流れが再び表面に付着するため、分離ゾーンが局所的になることがある（図4aを参照）。 流れが本体の後縁から（例えば、翼の後縁から）分離する場合、いわゆる後流は「リンク」境界層によって形成される（図4b参照）。
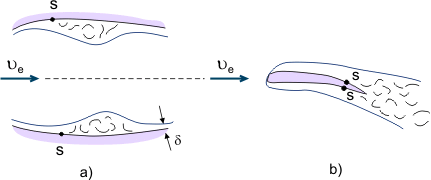
図4.後流の形成。 境界層分離現象.
Prandtl, L. (1904) Über Flüssingkeitsbewegungbeisehr Kleiner Reibung: Verhandl. III Int. Math. 3499>
Blasius, H. (1908) Grenzschichten in Flüssigkeiten mit Kleiner Reibung: Z. Math. Phys., 56:1-37.
Kutateladze, S. S. and Leontiev, A. I. (1990) Heat Transfer, Mass Transfer and Turbulent Boundary Layer, Hemisphere Publishing Corporation, New York, Washington, Philadelphia, London.
。